IB DP PHYSICS 2025 SL&HL – Study notes- All Topics
Topic 4.1 Kinematics of rotational motion
Topic 1 Weightage : XX
Notes for 4.1 Kinematics of rotational motion – Only for Higher Level (HL)
torque τ of a force about an axis as given by τ = Fr sin θ, rotational equilibrium, unbalanced torque, angular acceleration, angular displacement, angular velocity, equations of motion for uniform angular acceleration, moment of inertia, Newton’s second law for rotation, angular momentum, resultant torque, kinetic energy of rotational motion
- IB DP Physics 2025 SL- IB Style Practice Questions with Answer-Topic Wise-Paper 1
- IB DP Physics 2025 HL- IB Style Practice Questions with Answer-Topic Wise-Paper 1
- IB DP Physics 2025 SL- IB Style Practice Questions with Answer-Topic Wise-Paper 2
- IB DP Physics 2025 HL- IB Style Practice Questions with Answer-Topic Wise-Paper 2
Learning Objectives
Students should understand:
• the torque τ of a force about an axis as given by τ = Fr sin θ
• that bodies in rotational equilibrium have a resultant torque of zero
• that an unbalanced torque applied to an extended, rigid body will cause angular acceleration
• that the rotation of a body can be described in terms of angular displacement, angular velocity and angular acceleration
• that equations of motion for uniform angular acceleration can be used to predict the body’s angular position θ, angular displacement Δθ, angular speed ω and angular acceleration α, as given by
\(Δθ =\frac{ω_f + ω_i}{2}t\)
\(ω_f = ω_i + αt\)
\(Δθ = ω_it +\frac{1}{2} αt^2\)
\(ω_f^2 = ω_i^2 + 2αΔθ\)
• that the moment of inertia I depends on the distribution of mass of an extended body about an axis of rotation
• the moment of inertia for a system of point masses as given by \(I = Σmr^2\)
• Newton’s second law for rotation as given by τ = Iα where τ is the average torque
• that an extended body rotating with an angular speed has an angular momentum L as given by L = Iω
• that angular momentum remains constant unless the body is acted upon by a resultant torque
• that the action of a resultant torque constitutes an angular impulse ΔL as given by ΔL = τΔt = Δ(Iω),
• the kinetic energy of rotational motion as given by \(E_k=\frac{1}{2}Iω^2= \frac{L^2}{2I}\)
8.1 Rotational Motion and Angular Displacement
| In the simplest kind of rotation, points on a rigid object move on circular paths around an axis of rotation. |  |
The angle through which the object rotates is called the angular displacement. \(Δθ = θ- θ_o\) |  |
The angle through which the object rotates is called the angular displacement. \(Δθ = θ- θ_o\) |
 |
8.1 Rotational Motion and Angular Displacement

In the simplest kind of rotation,
points on a rigid object move on
circular paths around an axis of rotation.
DEFINITION OF ANGULAR DISPLACEMENT
When a rigid body rotates about a fixed axis, the angular displacement is the angle swept out by a line passing through any point on the body and intersecting the axis of rotation perpendicularly.
By convention, the angular displacement is positive if it is counterclockwise and negative if it is clockwise.

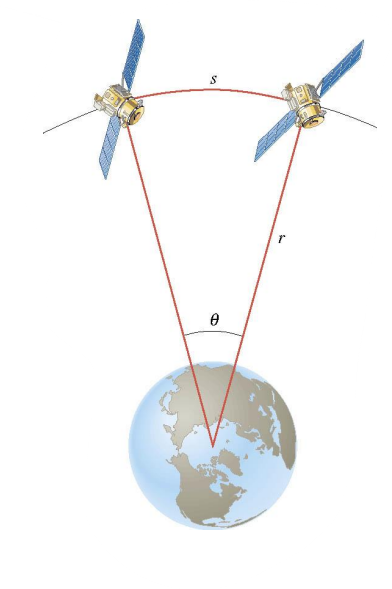
\(θ (in\;radians)= \frac{Arc\;length}{Radius}=\frac{s}{r}\)

For a full revolution:
\(θ=\frac{2πr}{r} = 2π rad = 2 π rad = 360°\)
Example 1 Adjacent Synchronous Satellites
Synchronous satellites are put into an orbit whose radius is \(4.23×10^7\)m.
If the angular separation of the two satellites is 2.00 degrees, find the arc length that separates them.