Question
A ball of mass 0.800kg is attached to a string. The distance to the centre of the mass of the ball from the point of support is 95.0cm. The ball is released from rest when the string is horizontal. When the string becomes vertical the ball collides with a block of mass 2.40kg that is at rest on a horizontal surface.
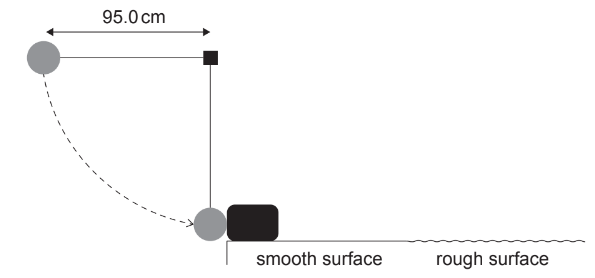
(a) Just before the collision of the ball with the block,
(i) draw a free-body diagram for the ball. [2]
(ii) show that the speed of the ball is about \(4.3 \mathrm{~ms}^{-1}\). [1]
(iii) determine the tension in the string. [2]
(b) After the collision, the ball rebounds and the block moves with speed 2.16ms-1.
(i) Show that the collision is elastic. [4]
(ii) Calculate the maximum height risen by the centre of the ball. [2]
(c) The coefficient of dynamic friction between the block and the rough surface is 0.400.
Estimate the distance travelled by the block on the rough surface until it stops. [3]
▶️Answer/Explanation
Ans:
a(i) Tension upwards, weight downwards \(\checkmark\) Tension is clearly longer than weight \(\checkmark\)
( ii )\(v=\sqrt{2 \times 9.81 \times 0.95}\) OR \(=4.32 \mathrm{kms}^{-1} n\)
iii \(\begin{aligned} & T-m g=F_{\text {net }} O R \quad T-m g=\frac{m v^2}{r} \checkmark \\ & T \ll=0.800 \times 9.81+\frac{0.800 \times 4.317^2}{0.95} \otimes=23.5 \ll \mathrm{Nw}\end{aligned}\)
b i Use of conservation of momentum.
Rebound speed \(=2.16 \propto \mathrm{m} \mathrm{s}^{-1}\) w
Calculation of initial KE \(=* \frac{1}{2} \times 0.800 \times 4.317^2 n=7.46 * \mathrm{~J}\)
Calculation of final KE \(=\propto \frac{1}{2} \times 0.800 \times 2.16^2+\frac{1}{2} \times 2.40 \times 2.16^2 n=7.46 \propto \mathrm{J} »\) shence elastic”
b ii ALTERNATIVE 1
Rebound speed is halved so energy less by a factor of \(4 \checkmark\) Hence height is \(\frac{95}{4}=23.8 \% \mathrm{~cm} \otimes\)
ALTERNATIVE 2
Use of conservation of energy / \(\frac{1}{2} \times 0.800 \times 2.16^2=0.800 \times 9.8 \times h\) OR
Use of proper kinematics equation (e.g. \(0=2.16^2-2 \times 9.8 \times h\) ) \(h=23.8 * \mathrm{~cm} \otimes\)
c.ALTERNATIVE 1
Frictional force is \(f \ll=0.400 \times 2.40 \times 9.81 »=9.42 * N \cdots v\)
\(9.42 \times d=\frac{1}{2} \times 2.40 \times 2.16^2\) OR \(d=\frac{5.5987}{9.42}\)
\(d=0.594 \ll \mathrm{m} » \checkmark\)
ALTERNATIVE 2
$
a=\ll \frac{f}{m}=\mu g=0.4 \times 9.81=» 3.924 \ll \mathrm{m} \mathrm{s}^{-2}{ }_w \checkmark
$
Proper use of kinematics equation(s) to determine
$
d=0.594 \ll \mathrm{m} »
$
Impulse and momentum
The diagram shows an arrangement used to test golf club heads.
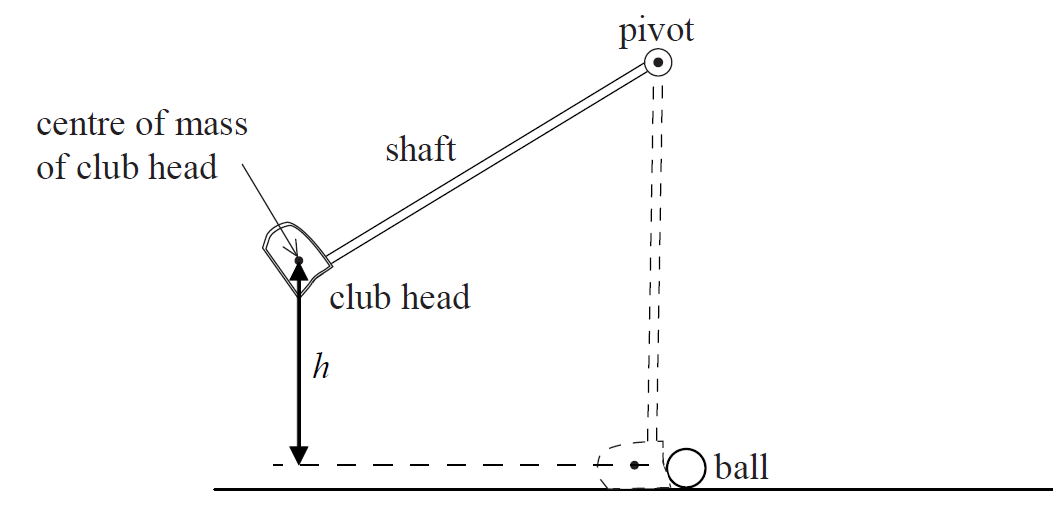
The shaft of a club is pivoted and the centre of mass of the club head is raised by a height h before being released. On reaching the vertical position the club head strikes the ball.
a. (i) Describe the energy changes that take place in the club head from the instant the club is released until the club head and the ball separate.
(ii) Calculate the maximum speed of the club head achievable when h = 0.85 m. [4]
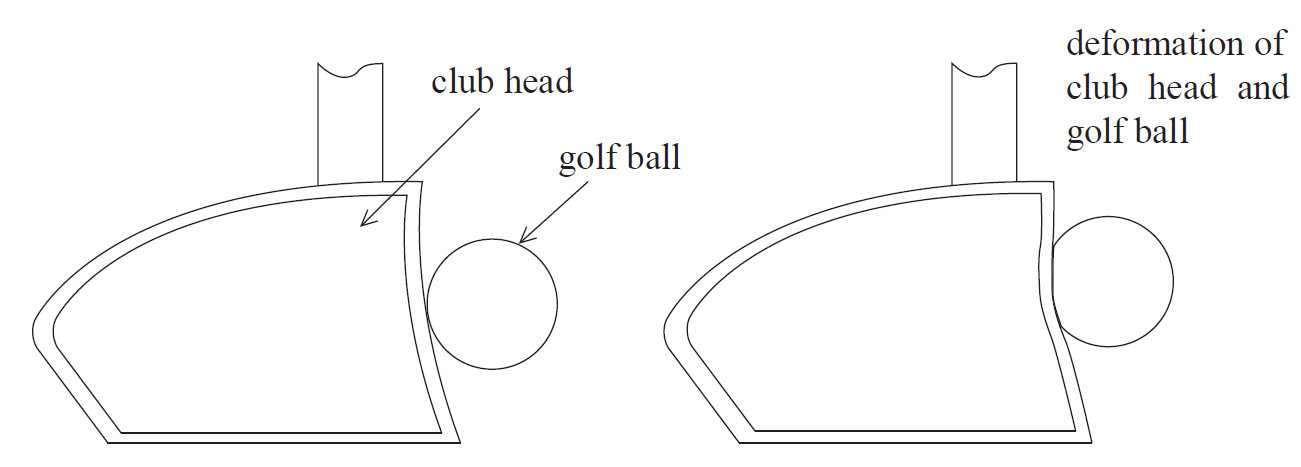
Explain how increasing the deformation of the club head may be expected to increase the speed at which the ball leaves the club. [2]
In a different experimental arrangement, the club head is in contact with the ball for a time of 220 μs. The club head has mass 0.17 kg and the ball has mass 0.045 kg. At the moment of contact the ball is at rest and the club head is moving with a speed of 38 ms–1. The ball moves off with an initial speed of 63 ms–1.
(i) Calculate the average force acting on the ball while the club head is in contact with the ball.
(ii) State the average force acting on the club head while it is in contact with the ball.
(iii) Calculate the speed of the club head at the instant that it loses contact with the ball. [5]
Answer/Explanation
Markscheme
a. (i) (gravitational) potential energy (of club head) goes to kinetic energy (of club head);
some kinetic energy of club head goes to internal energy of club head/kinetic energy of ball;
(ii) equating mgh to \(\frac{1}{2}\)mv2 ;
v=4.1(ms-1);
Award [0] for answers using equation of motion – not uniform acceleration.
deformation prolongs the contact time;
increased impulse => bigger change of momentum/velocity;
or
(club head) stores (elastic) potential energy on compression;
this energy is passed to the ball;
(i) any value of \(\frac{{{\rm{mass}} \times {\rm{velocity}}}}{{{\rm{time}}}}\);
1.3 x 104 (N);
(ii)-1.3 x 10-4 (N);
Accept statement that force is in the opposite direction to (c)(i).
Allow the negative of any value given in (c)(i).
(iii) clear use of conservation of momentum / impulse = change of momentum;
21(ms-1 );
or
a=\(\left( {\frac{{\rm{F}}}{{\rm{m}}} = \frac{{ – 13000}}{{0.17}} = } \right)\left( – \right)76500\left( {{\rm{m}}{{\rm{s}}^{ – 1}}} \right)\);
v=(u+at=38-76500 x 0.00022=) 21(ms-1);
Award [2] for a bald correct answer.
Examiners report
a. (i) Nearly all candidates gained a mark for recognising the change from kinetic to potential energy in this part. Fewer recognised that the club head would not transfer all of its energy to the ball and therefore retained a significant amount of energy.
(ii) This part was well done by many.
A minority of candidates became bogged down by the deformation of the ball and club head idea and ventured into elastic potential energy ideas. This had a successful outcome in many cases when there was discussion of the compression providing further kinetic energy to the ball on recovering its shape. The most straightforward solution was to use to principle of impulse being equal to the change in momentum (as shown in the question heading) and simply to recognise that an increased contact time would be expected to give a greater change of momentum for a constant force.
(i) This was well done with the only real problem being deciding which was the speed change of the ball.
(ii) Less candidates than anticipated recognised that the force on the club head was equal and opposite to that acting on the ball (applying Newton’s third law of motion).
(iii) Most made a good attempt at calculating the speed of the club head.
This question is in two parts. Part 1 is about power and efficiency. Part 2 is about electrical resistance.
Part 1 Power and efficiency
A bus is travelling at a constant speed of 6.2 m s–1 along a section of road that is inclined at an angle of 6.0° to the horizontal.
a. (i) The bus is represented by the black dot shown below. Draw a labelled sketch to represent the forces acting on the bus.

(ii) State the value of the rate of change of momentum of the bus. [5]
The engine of the bus suddenly stops working.
(i) Determine the magnitude of the net force opposing the motion of the bus at the instant at which the engine stops.
Answer/Explanation
Markscheme
a (i)

identification of normal reaction/N and weight/W;
identification of friction and driving force;
correct directions of all four forces;
correct relative lengths; { (friction ≅ driving force and N ≅ W but N must not be longer than W) (judge by eye)
(ii) zero;
input power =\(\frac{{{\rm{output power}}}}{{{\rm{efficiency}}}} = \frac{{70}}{{0.35}}\);
= 200 kW;
Award [2] for a bald correct answer.
height gained in 1s=(6.2 sin 6=) 0.648(m);
rate of change of PE=8.5×103×9.81×0.648;
=5.4×104W;
power used to overcome friction=(7×104−5.4×104=)1.6×104(W); {(allow ECF from (c))
\(F = \left( {\frac{p}{v} = } \right)\frac{{1.6 \times {{10}^4}}}{{6.2}}\);
=2.6kN;
(i) component of weight down slope = 8.5×103×9.81 sin 6;
net force=2.6×103+8.5×103×9.81 sin 6
=11kN;
Watch for ECF from (d).
(ii) air resistance decreases as speed drops;
so net force decreases;
Examiners report
a (i) Diagrams were poorly presented and ill-thought. 4 marks were assigned to this and candidates should have given much more care to it. Marks were given for appropriate descriptions, directions and lengths of the vectors. In particular, candidates should recognize that the term “acceleration” will not do for a driving force, and that “normal” simply implies “at 90°”. The essential point about the upwards force from the surface is that it is a reaction force.
This question is in two parts. Part 1 is about momentum change. Part 2 is about an oscillating water column (OWC) energy converter.
Part 1 Momentum change
a. State the law of conservation of linear momentum.
Gravel falls vertically onto a moving horizontal conveyor belt.

(i) The gravel falls at a constant rate of 13 kg s–1 through a height of 1.9 m. Show that the vertical speed of the gravel as it lands on the conveyor belt is about 6 m s–1.
(ii) The gravel lands on the conveyor belt without rebounding. Calculate the rate of change of the vertical momentum of the gravel.
(iii) Gravel first reaches the belt at t = 0.0 s and continues to fall. Determine the total vertical force that the gravel exerts on the conveyor belt at t = 5.0 s. [7]
The conveyor belt moves with a constant horizontal speed of 1.5 m s–1. As the gravel lands on the belt, it has no horizontal speed.
(i) Calculate the rate of change of the kinetic energy of the gravel due to its change in horizontal speed.
(ii) Determine the power required to move the conveyor belt at constant speed.
(iii) Outline why the answers to (c)(i) and (ii) are different. [4]
Answer/Explanation
Markscheme
a. if no external forces act / isolated system;
momentum is constant / (total) momentum before=(total) momentum after;
(i) use of \(v = \sqrt {2gh} \);
6.11ms–1; (must show calculation to better than 1 sf)
(ii) rate of change of vertical momentum=13×6.11;
79N; (accept answers in the range of 78N to 80N)
(iii) mass accrued=5.0×13=65kg;
weight of this mass (=65×9.8)=637N; (650 from g=10ms–2)
total force (637+79=)716N; } (allow ECF from (b)(ii) and from incorrect weight)
(i) 14.6Js–1;
(ii) horizontal momentum gain per second =13×1.5( =19.5kgms–1);
power required=29.3W;
(iii) additional energy/power required to accelerate gravel (through friction at the surface of the belt) / the gravel has to slip to gain horizontal speed / OWTTE