Simple harmonic motion and forced oscillations
The graph shows the variation with time of the displacement of an object undergoing simple harmonic motion.
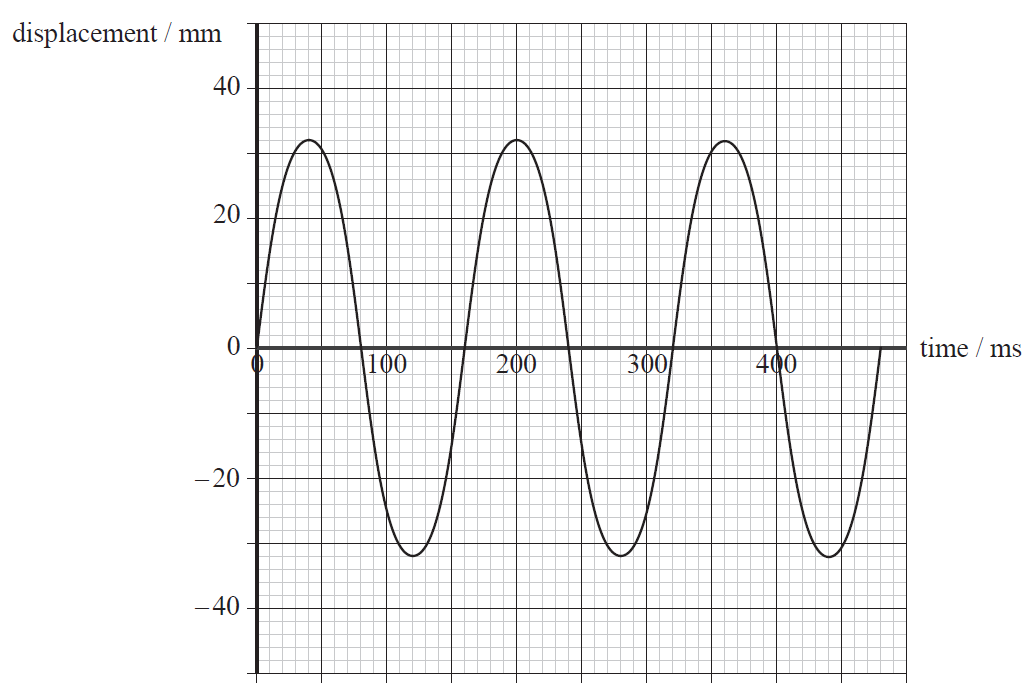
a
(i) State the amplitude of the oscillation.
(ii) Calculate the frequency of the oscillation.
(i) Determine the maximum speed of the object.
(ii) Determine the acceleration of the object at 140 ms.
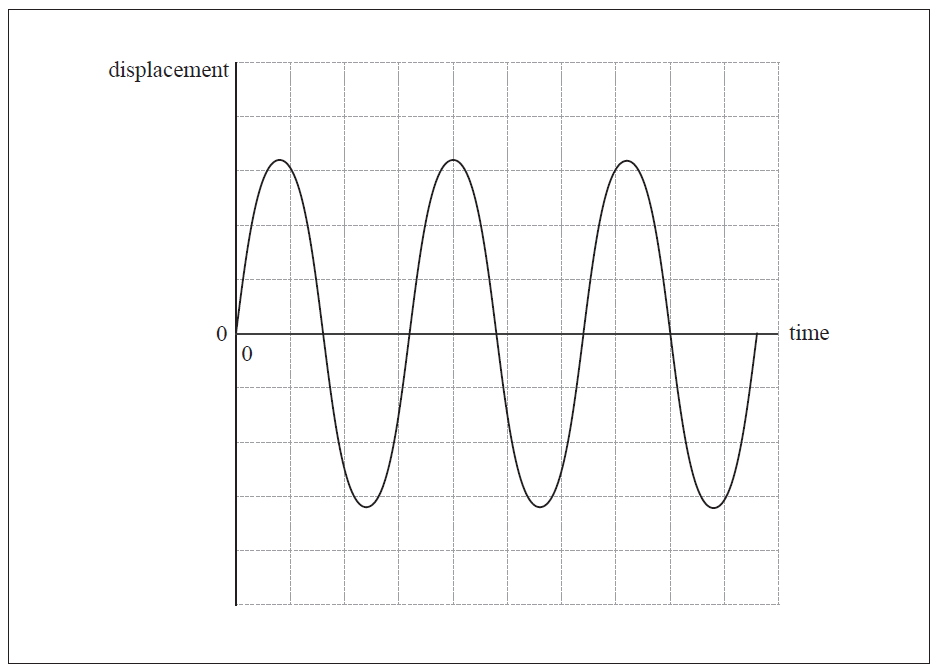
The graph below shows how the displacement of the object varies with time. Sketch on the same axes a line indicating how the kinetic energy of the object varies with time.
You should ignore the actual values of the kinetic energy.
Answer/Explanation
Markscheme
a
(i) 32 (mm);
(ii) period = 160 (ms);
frequency = 6.2/6.3 (Hz);
Allow ECF for incorrect period.
(i) ω=2π×6.25;
v(=39.3×32×10-3)=1.3(ms-1); (allow ECF from (a))
or
tangent drawn to graph at a point of zero displacement;
gradient calculated between 1.2 and 1.4;
(ii) displacement = 23–26 (mm);
35–40 (ms-2);
23 mm found by calculating displacement
double frequency;
always positive and constant amplitude;
correct phase ie cosine squared;
Ignore amplitude value.
A minimum of one complete, original oscillation needed to award [3].
a
(i) Nearly all candidates correctly stated the amplitude as being 32 mm.
(ii) Most were able to measure the period and many then went on to calculate the frequency with the occasional hiccup with conversion of ms into kHz etc.
(i) A large proportion of candidates correctly determined the maximum speed of the object by correctly calculating the angular speed and multiplying it by the amplitude. Full marks were awarded to those calculating the gradient of the tangent to the displacement-time graph at zero displacement.
(ii) In the simplest route to the answer candidates were usually successful in measuring the displacement at 140 ms and then using the defining equation for SHM to calculate the acceleration. Other routes were allowed as alternatives but success was infrequent.
Given the relative difficulty of transposing the displacement into a velocity and then squaring it to find the shape of the kinetic energy function, this part was done very well. Most candidates recognised that the energy was always positive, of twice the frequency of the displacement graph and took a cosine squared shape. Sketches were of variable quality but often better than others on the paper.
Part 2 Simple harmonic oscillations
A longitudinal wave travels through a medium from left to right.
Graph 1 shows the variation with time t of the displacement x of a particle P in the medium.
Graph 1

a.
For particle P,
(i) state how graph 1 shows that its oscillations are not damped.
(ii) calculate the magnitude of its maximum acceleration.
(iii) calculate its speed at t=0.12 s.
(iv) state its direction of motion at t=0.12 s.
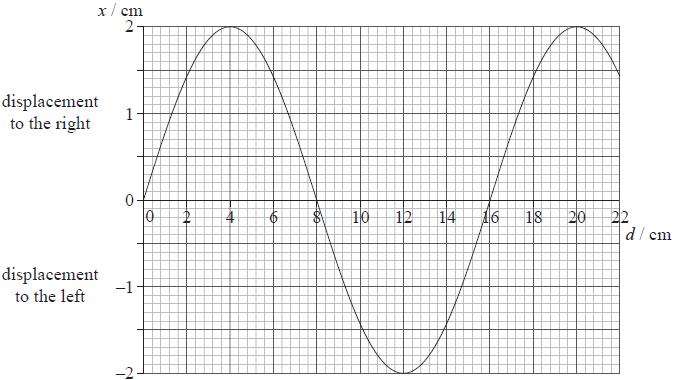
Graph 2 shows the variation with position d of the displacement x of particles in the medium at a particular instant of time.
Graph 2

Determine for the longitudinal wave, using graph 1 and graph 2,
(i) the frequency.
(ii) the speed.
Graph 2 – reproduced to assist with answering (c)(i).
(c) The diagram shows the equilibrium positions of six particles in the medium.
![]()
(i) On the diagram above, draw crosses to indicate the positions of these six particles at the instant of time when the displacement is given by graph 2.
(ii) On the diagram above, label with the letter C a particle that is at the centre of a compression.
Answer/Explanation
Markscheme
a.
(i) the amplitude is constant;
(ii) period is 0.20s;
\({a_{\max }} = \left( {{{\left[ {\frac{{2\pi }}{T}} \right]}^2}{x_0} = {{31.4}^2} \times 2.0 \times {{10}^{ – 2}}} \right) = 19.7 \approx 20{\rm{m}}{{\rm{s}}^{ – 2}}\)
Award [2] for correct bald answer and ignore any negative signs in answer.
(iii) displacement at t = 0.12cm is (−)1.62cm;
\(v\left( { = \frac{{2\pi }}{T}\sqrt {{x_0} – {x^2}} } \right) = 31.4\sqrt {\left( {2.0 \times {{10}^{ – 2}}} \right)^2 – {{\left( {1.62 \times {{10}^{ – 2}}} \right)}^2}} = 0.37{\rm{m}}{{\rm{s}}^{ – 1}}\);
Accept displacement in range 1.60 to 1.70 cm for an answer in range 0.33ms−1 to 0.38ms−1.
or
\({v_0} = \frac{{2\pi }}{T}{x_0} = 0.628{\rm{m}}{{\rm{s}}^{ – 1}}\);
\(\left| {\left. v \right|} \right. = \left( {\left| {\left. { – {v_0}\sin \left[ {\frac{{2\pi }}{T}t} \right]} \right|} \right. \Rightarrow \left| {\left. v \right|} \right. = \left| {\left. { – 0.628\sin \left[ {31.4 \times 0.12} \right]} \right|} \right. = \left| {\left. {0.37} \right|} \right.} \right) = 0.37{\rm{m}}{{\rm{s}}^{ – 1}}\);
or
drawing a tangent at 0.12s;
measurement of slope of tangent;
Accept answer in range 0.33ms−1 to 0.38ms−1 .
(i) use of \(f = \frac{1}{T}\);
and so \(f\left( { = \frac{1}{{0.20}}} \right) = 5.0{\rm{Hz}}\);
(ii) wavelength is 16cm;
and so speed is v(=fλ=5.0×0.16)=0.80ms−1;
(i) points at 0, 8 and 16 cm stay in the same place;
points at 4 and 20 cm move 2 cm to the right;
point at 12 cm moves 2 cm to the left;
(ii) the point at 8 cm;