Question
(a) A transverse water wave travels to the right. The diagram shows the shape of the surface of the water at time \(t=0 . \mathrm{P}\) and \(\mathrm{Q}\) show two corks floating on the surface.

(i) State what is meant by a transverse wave.[1]
(ii) The frequency of the wave is \(0.50 \mathrm{~Hz}\). Calculate the speed of the wave.[1]
(iii) Plot on the diagram the position of \(\mathrm{P}\) at time \(t=0.50 \mathrm{~s}\).[1]
(iv) Show that the phase difference between the oscillations of the two corks is \(\pi\) radians.[1]
(b) Monochromatic light is incident on two very narrow slits. The light that passes through the slits is observed on a screen. \(M\) is directly opposite the midpoint of the slits. \(x\) represents the displacement from \(\mathrm{M}\) in the direction shown.

A student argues that what will be observed on the screen will be a total of two bright spots opposite the slits. Explain why the student’s argument is incorrect. [2]
(c) The graph shows the actual variation with displacement \(x\) from \(M\) of the intensity of the light on the screen. \(I_0\) is the intensity of light at the screen from one slit only.

(i) Explain why the intensity of light at \(x=0\) is \(4 I_0\).[2]
(ii) The slits are separated by a distance of \(0.18 \mathrm{~mm}\) and the distance to the screen is \(2.2 \mathrm{~m}\). Determine, in \(\mathrm{m}\), the wavelength of light.[2]
(iii) The two slits are replaced by many slits of the same separation. State one feature of the intensity pattern that will remain the same and one that will change.[2]
Stays the same:…………………………………………………………………………………………………….
Changes:……………………………………………………………………………………………………………….
(d) (i) Two sources are viewed though a single slit. The graph shows the diffraction pattern of one source.

Sketch, on the axes, the diffraction pattern of the second source when the images of the two sources are just resolved according to the Rayleigh criterion.[1]
(ii) Centaurus \(\mathrm{A}\) is a galaxy a distance of \(1.1 \times 10^{23} \mathrm{~m}\) away. A radio telescope of diameter \(300 \mathrm{~m}\) operating at a wavelength of \(3.2 \mathrm{~cm}\) is used to observe the galaxy. Determine the minimum size of the radio emitting region of the galaxy that can be resolved by this telescope.[2]
▶️Answer/Explanation
Ans:
a i «A wave where the displacement of particles/oscillations of particles/movement of particles/vibrations of particles is perpendicular/normal to the direction of energy transfer/wave travel/wave velocity/wave movement/wave propagation
a ii \(V=\alpha 0.50 \times 16=» 8.0 \ll \mathrm{ms}^{-1}\)
iv ALTERNATIVE 1
Phase difference is \(\frac{2 \pi}{\lambda} \times \frac{\lambda}{2}\) \(\alpha=\pi_b\)
ALTERNATIVE 2
One wavelength/period represents «phase difference» of \(2 \pi\) and «corks» are \(1 / 2\) wavelength/period apart so phase difference is \(\pi / O W T T E \checkmark\)
b.light acts as a wave «and not a particle in this situation» light at slits will diffract / create a diffraction pattern light passing through slits will interfere / create an interference pattern \&creating bright and dark spots»
c i The amplitude «at \(x=0\) will be doubled \(\checkmark\) intensity is proportional to amplitude squared / I \(\propto A^2 \checkmark\)
c ii Use of \(s=\frac{\lambda D}{d} \Rightarrow \lambda=\frac{s d}{D}\) OR \(s=\frac{n \lambda D}{d} \Rightarrow \lambda=\frac{s d}{n D}\)
$
\lambda=\ll \frac{0.567 \times 10^{-2} \times 0.18 \times 10^{-3}}{2.2}=» 4.6 \times 10^{-7} \ll \mathrm{mm}
$
iii Stays the same: Position/location of maxima/distance/separation between maxima «will be the same» / OWTTE \(\checkmark\)
Changes: Intensity/brightness/width/sharpness «of maxima will changew/ OWTTE \(\checkmark\)
d i . Maximum coinciding with first minimum \(A N D\) minimum coinciding with maximum \(\checkmark\)
d ii ALTERNATIVE 1
$
\begin{aligned}
& \frac{d}{D}=1.22 \times \frac{\lambda}{b} \text { therefore } d=\frac{1.22 \times \lambda \times D}{b} \\
& \varangle d \approx 1.22 \times \frac{3.2 \times 10^{-2} \times 1.1 \times 10^{23}}{300},=1.4 \times 10^{+9} \alpha \mathrm{m} *
\end{aligned}
$
ALTERNATIVE 2
$
\begin{aligned}
& \theta=\kappa 1.22 \frac{\lambda}{b}=1.22 \times \frac{3.2 \times 10^{-2}}{300}=» 1.3 \times 10^{-4} \text { «radians } » \\
& \mathrm{~d}=\alpha\left(1.1 \times 10^{23}\right)\left(1.3 \times 10^{-4}\right)=» 1.4 \times 10^{19} \ll \mathrm{m} »
\end{aligned}
$
Question
This question is in two parts. Part 1 is about wave motion. Part 2 is about the melting of the Pobeda ice island.
Part 1 Wave motion
a.
State what is meant by the terms ray and wavefront and state the relationship between them.
The diagram shows three wavefronts, A, B and C, of a wave at a particular instant in time incident on a boundary between media X and Y. Wavefront B is also shown in medium Y.

(i) Draw a line to show wavefront C in medium Y.
(ii) The refractive index of X is nX and the refractive index of Y is nY. By making appropriate measurements, calculate \(\frac{{{n_{\rm{X}}}}}{{{n_{\rm{Y}}}}}\).
Describe the difference between transverse waves and longitudinal waves.
The graph below shows the variation of the velocity v with time t for one oscillating particle of a medium.

(i) Calculate the frequency of oscillation of the particle.
(ii) Identify on the graph, with the letter M, a time at which the displacement of the particle is a maximum.
Answer/Explanation
Markscheme
a.
ray: direction of wave travel / energy propagation;
wavefront: line that joins points with same phase/of same crest/trough;
ray normal/at right angles/perpendicular to wavefront;
(i) line parallel to existing line in Y and continuous at boundary; (both needed)
(ii) measures “wavelength” correctly in media X and Y; } (by eye)
(look for ratio of 0.5: 1 in responses)
\(\frac{{{n_{\rm{X}}}}}{{{n_{\rm{Y}}}}} = \frac{{{\lambda _{\rm{Y}}}}}{{{\lambda _{\rm{X}}}}}\);
0.5:1; (accept answers in the range of 0.47 to 0.53)
or
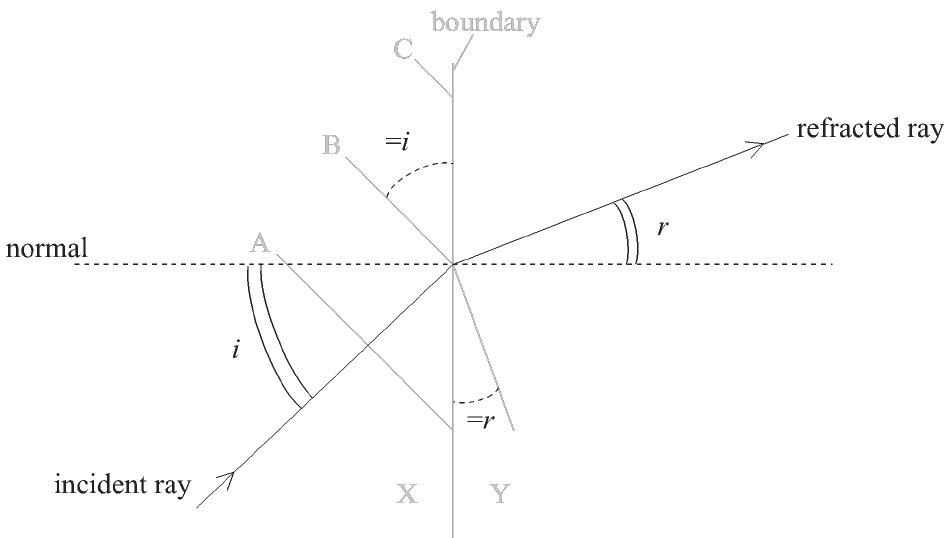
justification that angles needed for calculation are either pair of i and r as shown and angles measured correctly;
\(\frac{{{n_{\rm{X}}}}}{{{n_{\rm{Y}}}}} = \frac{{\sin r}}{{\sin i}}\);
0.5:1;
mention of perpendicular/right angle/90° angle for transverse and parallel for longitudinal;
clear comparison between direction of energy propagation and direction of vibration/oscillation of particles for both waves;
(i) time period=6.0ms;
167Hz;
(ii) M where line crosses x-axis;
(iii) counts rectangles (14±2) to first peak;
one rectangle equivalent to 0.5 mm;
7.2 mm;
or
\(\omega = \left( {2\pi f = } \right)330\pi \);
\(a = \left( {\frac{v}{w} = } \right)\frac{{7.5}}{{330\pi }}\);
7.2 mm;