Question
On a guitar, the strings played vibrate between two fixed points. The frequency of vibration is modified by changing the string length using a finger. The different strings have different wave speeds. When a string is plucked, a standing wave forms between the bridge and the finger.
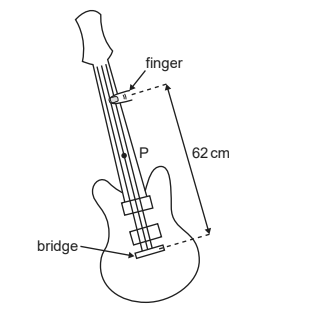
(a) Outline how a standing wave is produced on the string. [2]
(b) The string is displaced 0.4 cm at point P to sound the guitar. Point P on the string vibrates with simple harmonic motion (shm) in its first harmonic with a frequency of 195 Hz. The sounding length of the string is 62 cm.
(i) Show that the speed of the wave on the string is about 240 m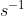 
. [2]
(ii) Sketch a graph to show how the acceleration of point P varies with its displacement from the rest position. [1]
(iii) Calculate, in m 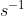, the maximum velocity of vibration of point P when it is vibrating with a frequency of 195 Hz. [2]
(iv) Calculate, in terms of g, the maximum acceleration of P. [2]
(v) Estimate the displacement needed to double the energy of the string. [2]
(c) The string is made to vibrate in its third harmonic. State the distance between consecutive nodes. [1]
Answer/Explanation
Ans:
a «travelling» wave moves along the length of the string and reflects «at fixed end» superposition/interference of incident and reflected waves the superposition of the reflections is reinforced only for certain wavelengths
b i λ = 2 l = 2 × 0.62 = «1.24 m» v = f λ = 195 ×1.24 = 242 «m s-1» Answer must be to 3 or more sf or working shown for MP2
b ii straight line through origin with negative gradient
b iii max velocity occurs at x 0 = V= «(2π)(195) \(\sqrt{0.004^{2}}\) » = 4.9«ms-1 »
b iv a = (2π 195)2 × 0.004 = 6005 «m s−2 » = 600g v use of E =A 2 RO Xo2 A = 0.4 = 0.57 «cm» ≅ 0.6 «cm»
c \(\frac{62}{3}\) = 21«cm»
A large cube is formed from ice. A light ray is incident from a vacuum at an angle of 46˚ to the normal on one surface of the cube. The light ray is parallel to the plane of one of the sides of the cube. The angle of refraction inside the cube is 33˚.
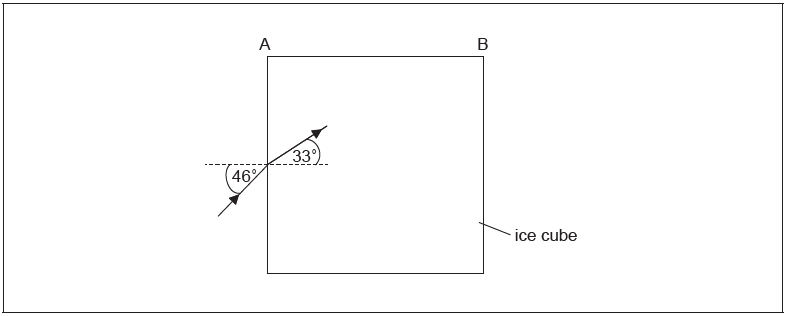
Each side of the ice cube is 0.75 m in length. The initial temperature of the ice cube is –20 °C.
a.i. Calculate the speed of light inside the ice cube.[2]
Specific latent heat of fusion of ice = 330 kJ kg–1
Specific heat capacity of ice = 2.1 kJ kg–1 k–1
Density of ice = 920 kg m–3[4]
▶️Answer/Explanation
Markscheme
a.i.
«v = c\(\frac{{{\text{sin }}i}}{{{\text{sin }}r}}\) =» \(\frac{{3 \times {{10}^8} \times {\text{sin}}\left( {33} \right)}}{{{\text{sin}}\left( {46} \right)}}\)
2.3 x 108 «m s–1»
light strikes AB at an angle of 57°
critical angle is «sin–1\(\left( {\frac{{2.3}}{3}} \right)\) =» 50.1°
49.2° from unrounded value
angle of incidence is greater than critical angle so total internal reflection
OR
light strikes AB at an angle of 57°
calculation showing sin of “refracted angle” = 1.1
statement that since 1.1>1 the angle does not exist and the light does not emerge[Max 3 marks]
total internal reflection shown
ray emerges at opposite face to incidence
Judge angle of incidence=angle of reflection by eye or accept correctly labelled angles
With sensible refraction in correct direction
mass = «volume x density» (0.75)3 x 920 «= 388 kg»
energy required to raise temperature = 388 x 2100 x 20 «= 1.63 x 107 J»
energy required to melt = 388 x 330 x 103 «= 1.28 x 108 J»
1.4 x 108 «J» OR 1.4 x 105 «kJ»
Accept any consistent units
Award [3 max] for answer which uses density as 1000 kg–3 (1.5× 108 «J»)
in solid state, nearest neighbour molecules cannot exchange places/have fixed positions/are closer to each other/have regular pattern/have stronger forces of attraction
in liquid, bonds between molecules can be broken and re-form
OWTTE
Accept converse argument for liquids[Max 1 Mark]