Question
A ball is projected at an angle to the horizontal on Earth reaching a maximum height H and a maximum range R. The same ball is projected at the same angle and speed on a planet where the acceleration due to gravity is three times that on Earth. Resistance effects are negligible.
What is the maximum range and the maximum height reached on that planet?
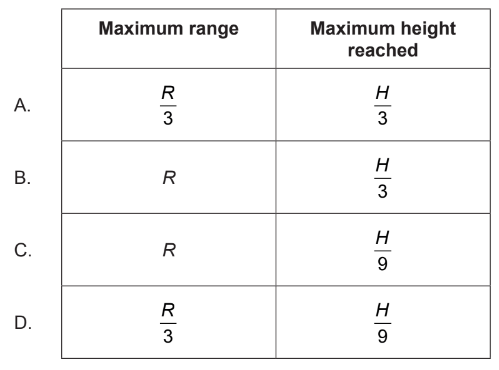
▶️Answer/Explanation
Ans:A
Let’s denote the following variables:
- \(H_e\): The maximum height reached on Earth.
- \(R_e\): The maximum range on Earth.
- \(H_p\): The maximum height reached on the planet with 3 times Earth’s gravity.
- \(R_p\): The maximum range on the planet with 3 times Earth’s gravity.
- \(g_e\): The acceleration due to gravity on Earth.
- \(g_p\): The acceleration due to gravity on the planet.
The maximum range \(R\) for a projectile launched at an angle \(\theta\) with an initial velocity \(V\) on a level surface can be calculated as:
\[R = \frac{V^2 \sin(2\theta)}{g}\]
where \(g\) is the acceleration due to gravity.
On Earth, we have \(g_e\) and \(R_e\), so for the Earth:
\[R_e = \frac{V^2 \sin(2\theta)}{g_e}\]
The maximum height \(H\) can be calculated as:
\[H = \frac{V^2 \sin^2(\theta)}{2g}\]
Now, on the planet with 3 times Earth’s gravity, the acceleration due to gravity is \(g_p = 3g_e\).
We know that the initial velocity and launch angle are the same on both Earth and the planet, so \(V\) and \(\theta\) are constant. We need to calculate \(R_p\) and \(H_p\).
For the planet:
Maximum range on the planet, \(R_p\):
\[R_p = \frac{V^2 \sin(2\theta)}{g_p} = \frac{V^2 \sin(2\theta)}{3g_e} = \frac{1}{3} \left(\frac{V^2 \sin(2\theta)}{g_e}\right) = \frac{1}{3} R_e\]
So, the maximum range on the planet is one-third of the maximum range on Earth.
Maximum height on the planet, \(H_p\):
\[H_p = \frac{V^2 \sin^2(\theta)}{2g_p} = \frac{V^2 \sin^2(\theta)}{2 \cdot 3g_e} = \frac{1}{3} \left(\frac{V^2 \sin^2(\theta)}{2g_e}\right) = \frac{1}{3} H_e\]
The maximum height on the planet is one-sixth of the maximum height on Earth.
So, on the planet with three times the acceleration due to gravity, the maximum range is one-third of the maximum range on Earth, and the maximum height is also one-third of the maximum height on Earth.
Question
The radius of the Earth is \(R\). A satellite is launched to a height \(h=\frac{R}{4}\) above the Earth’s surface. What is \(\frac{\text { gravitational force on satellite at the surface }}{\text { gravitational force on satellite at height } h}\) ?
A. \(\frac{4}{5}\)
B. \(\frac{16}{25}\)
C. \(\frac{25}{16}\)
D. \(\frac{5}{4}\)
▶️Answer/Explanation
Ans:C
The gravitational force between two objects is given by Newton’s law of universal gravitation, which states that the force is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. Mathematically, it’s represented as:
\[F = \frac{G \cdot m_1 \cdot m_2}{r^2}\]
In this case, we are comparing the gravitational force on a satellite at the Earth’s surface to the gravitational force on the satellite at a height \(h = \frac{R}{4}\) above the Earth’s surface. The only difference in the two cases is the distance from the center of the Earth.
1. For the gravitational force on the satellite at the Earth’s surface, the distance from the center of the Earth is \(R\).
2. For the gravitational force on the satellite at a height \(h\), the distance from the center of the Earth is \(R + h = R + \frac{R}{4} = \frac{5}{4}R\).
Now, we can calculate the ratio:
\[\frac{\text{gravitational force on satellite at surface}}{\text{gravitational force on satellite at height } h} = \frac{\frac{G \cdot m_{\text{satellite}} \cdot m_{\text{Earth}}}{R^2}}{\frac{G \cdot m_{\text{satellite}} \cdot m_{\text{Earth}}}{\left(\frac{5}{4}R\right)^2}}\]
Simplify this expression:
\[\frac{\frac{G \cdot m_{\text{satellite}} \cdot m_{\text{Earth}}}{R^2}}{\frac{G \cdot m_{\text{satellite}} \cdot m_{\text{Earth}}}{\frac{25}{16}R^2}} = \frac{1}{1} \cdot \frac{\frac{25}{16}}{1} = \frac{25}{16}\]
Question
The gravitational field strength at the surface of the Earth is often taken to be \(9.8 \mathrm{Nkg}^{-1}\).
The use of this value to calculate the weight of an object above the surface of the Earth is
A. a paradigm shift in our understanding of gravity.
B. an attempt to model gravitational fields.
C. an outcome from a peer review.
D. an approximation used for estimation purposes.
▶️Answer/Explanation
Ans:D
D. an approximation used for estimation purposes.
The use of \(9.8 \, \text{Nkg}^{-1}\) (approximately 9.8 m/s²) as the gravitational field strength at the surface of the Earth is a common approximation for estimation purposes. It simplifies calculations and provides a reasonable approximation for most everyday scenarios. However, it is not a paradigm shift, an attempt to model gravitational fields, or an outcome from a peer review. It is a practical value used to make calculations involving weight and gravity more manageable in common situations.
A satellite of mass 1500 kg is in the Earth’s gravitational field. It moves from a point where the gravitational potential is –30 MJ kg–1 to a point where the gravitational potential is –20 MJ kg–1. What is the direction of movement of the satellite and the change in its gravitational potential energy?

Answer/Explanation
Ans:A Gravitational potential is a negative quantity which increases when it move further , so the satellite is moving away from the earth.
Change in gravitational potential is
\(U_{f} – U_{i}= (-20) – (-30)=10\times 1500=15\times 10^{9}\rightarrow 15GJ\)
Two spherical objects of mass M are held a small distance apart. The radius of each object is r.

Point P is the midpoint between the objects and is a distance R from the surface of each object. What is the gravitational potential at point P?
A. \( – \frac{{GM}}{{{{\left( {r + R} \right)}^2}}}\)
B. \( – 2\frac{{GM}}{{r + R}}\)
C. \( – \frac{{GM}}{{r + R}}\)
D. 0
Answer/Explanation
Answer – B
Both are symmetrically placed
So , potential due to one \(=-\frac{GM}{R+r} \)
Due to both masses \(=-\frac{2GM}{R+r}\)