The two arrows in the diagram show the gravitational field strength vectors at the position of a planet due to each of two stars of equal mass M.
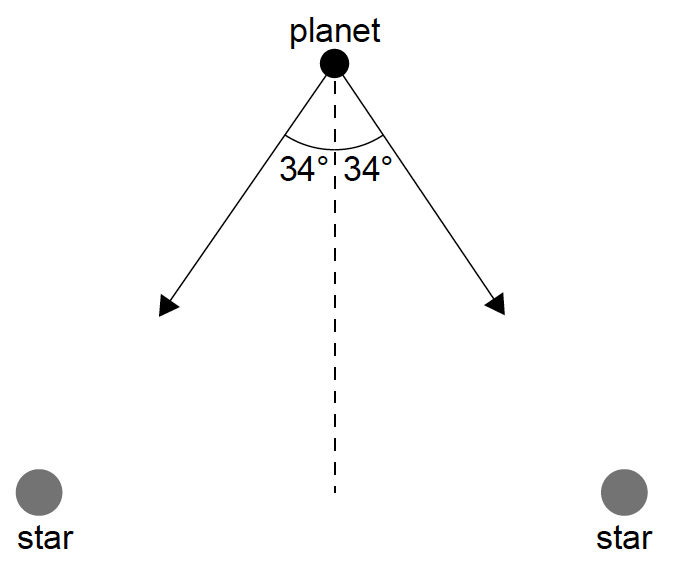
Each star has mass M=2.0×1030kg. The planet is at a distance of 6.0×1011m from each star.
a.
Show that the gravitational field strength at the position of the planet due to one of the stars is g=3.7×10–4Nkg–1.
Calculate the magnitude of the resultant gravitational field strength at the position of the planet.
Answer/Explanation
Markscheme
a.
\(g = \frac{{GM}}{{{r^2}}} = \frac{{6.67 \times {{10}^{ – 11}} \times 2.0 \times {{10}^{30}}}}{{{{\left( {6.0 \times {{10}^{11}}} \right)}^2}}}\)
OR
3.71×10-4Nkg−1
«gnet = 2cos34» 2g OR gcos34 OR gsin56 OR vector addition diagram shown
«gnet =«2×3.7×10−4 ×cos34o =» 6.1×10−4 Nkg
Part 2 Satellite
a.
State, in words, Newton’s universal law of gravitation.
The diagram shows a satellite orbiting the Earth. The satellite is part of the network of global-positioning satellites (GPS) that transmit radio signals used to locate the position of receivers that are located on the Earth.

When the satellite is directly overhead, the microwave signal reaches the receiver 67ms after it leaves the satellite.
(i) State the order of magnitude of the wavelength of microwaves.
(ii) Calculate the height of the satellite above the surface of the Earth
(i) Explain why the satellite is accelerating towards the centre of the Earth even though its orbital speed is constant.
(ii) Calculate the gravitational field strength due to the Earth at the position of the satellite.
Mass of Earth = 6.0×1024kg
Radius of Earth = 6.4×106m
(iii) Determine the orbital speed of the satellite.
(iv) Determine, in hours, the orbital period of the satellite.
Answer/Explanation
Markscheme
a.
force is proportional to product of masses and inversely proportional to square of distance apart;
reference to point masses;
(i) order of 1 cm;
(ii) 3×108×67×10−3;
2.0×107m;
(i) force required towards centre of Earth to maintain orbit;
force means that there is an acceleration / OWTTE;
or
direction changes;
a change in velocity therefore acceleration;
(ii) uses=\(\frac{{GM}}{{{r^2}}}\) or \(\frac{{6.7 \times {{10}^{ – 11}} \times 6.0 \times {{10}^{24}}}}{{{{\left[ {2.6 \times {{10}^7}} \right]}^2}}}\);
0.57Nkg–1; (allow ms–2)
(iii) \(v = \sqrt {0.57 \times \left( {2.0 \times {{10}^7} + 6.4 \times {{10}^6}} \right)} \) by equating \(\frac{{{v^2}}}{r}\) and g;
3900ms–1;
(iv) \(T = 2\pi \frac{{2.6 \times {{10}^7}}}{{3900}}\);