This question is about electric and magnetic fields.
A proton travelling to the right with horizontal speed 1.6×104ms–1 enters a uniform electric field of strength E. The electric field has magnitude 2.0×103NC–1 and is directed downwards.

a.
Calculate the magnitude of the electric force acting on the proton when it is in the electric field.
A uniform magnetic field is applied in the same region as the electric field. A second proton enters the field region with the same velocity as the proton in (a). This second proton continues to move horizontally.
(i) Determine the magnitude and direction of the magnetic field.
(ii) An alpha particle enters the field region at the same point as the second proton, moving with the same velocity. Explain whether or not the alpha particle will move in a straight line.
Answer/Explanation
Markscheme
=3.2×10-16(N);
(i) \(\left( {F = qvB \Rightarrow } \right)B = \frac{F}{{qv}}\) or \(\left( {Eq = qvB \Rightarrow } \right)B = \frac{E}{v}\);
\(\left( { = \frac{{3.2 \times {{10}^{ – 16}}}}{{1.6 \times {{10}^{ – 19}} \times 1.6 \times {{10}^4}}}} \right) = 0.13\) or 0.125(T);
directed into the page / OWTTE;
(ii) both electric and magnetic forces double / both forces increase by the same factor / both forces scale with q/charges and cancel;
so straight line followed; (only award if first mark awarded)
or
straight line followed if qE = qvB ⇒E v=B;
E, v and B constant (so straight line followed);
a.
This calculation was successfully done by the majority of candidates.
bi) The magnitude of the magnetic field was often successfully calculated, but few candidates were able to identify the direction. Most thought that it was in the opposite direction to the electric field, presumably confusing it with magnetic force.
bii) Many thought that it would carry on in a straight line but this was often based on spurious reasoning.
This question is in two parts. Part 1 is about electric fields and radioactive decay. Part 2 is about change of phase.
Part 1 Electric fields and radioactive decay
Part 2 Change of phase
a.
Define electric field strength.
A simple model of the proton is that of a sphere of radius 1.0×10–15m with charge concentrated at the centre of the sphere. Estimate the magnitude of the field strength at the surface of the proton.
Protons travelling with a speed of 3.9×106ms–1 enter the region between two charged parallel plates X and Y. Plate X is positively charged and plate Y is connected to earth.
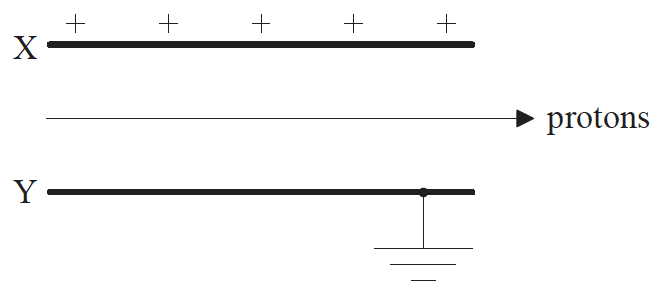
A uniform magnetic field also exists in the region between the plates. The direction of the field is such that the protons pass between the plates without deflection.
(i) State the direction of the magnetic field.
(ii) The magnitude of the magnetic field strength is 2.3×10–4T. Determine the magnitude of the electric field strength between the plates, stating an appropriate unit for your answer.
Protons can be produced by the bombardment of nitrogen-14 nuclei with alpha particles. The nuclear reaction equation for this process is given below.
\[{}_7^{14}{\rm{N}} + {}_2^4{\rm{He}} \to {\rm{X}} + {}_1^1{\rm{H}}\]
Identify the proton number and nucleon number for the nucleus X.
The following data are available for the reaction in (d).
Rest mass of nitrogen-14 nucleus =14.0031 u
Rest mass of alpha particle =4.0026 u
Rest mass of X nucleus =16.9991 u
Rest mass of proton =1.0073 u
Show that the minimum kinetic energy that the alpha particle must have in order for the reaction to take place is about 0.7 Me V.
A nucleus of another isotope of the element X in (d) decays with a half-life \({T_{\frac{1}{2}}}\) to a nucleus of an isotope of fluorine-19 (F-19).
(i) Define the terms isotope and half-life.
(ii) Using the axes below, sketch a graph to show how the number of atoms N in a sample of X varies with time t, from t=0 to \(t = 3{T_{\frac{1}{2}}}\). There are N0 atoms in the sample at t=0.

Water at constant pressure boils at constant temperature. Outline, in terms of the energy of the molecules, the reason for this.
In an experiment to measure the specific latent heat of vaporization of water, steam at 100°C was passed into water in an insulated container. The following data are available.
Initial mass of water in container = 0.300kg
Final mass of water in container = 0.312kg
Initial temperature of water in container = 15.2°C
Final temperature of water in container = 34.6°C
Specific heat capacity of water = 4.18×103Jkg–1K–1
Show that the data give a value of about 1.8×106Jkg–1 for the specific latent heat of vaporization L of water.
Explain why, other than measurement or calculation error, the accepted value of L is greater than that given in (h).
Answer/Explanation
Markscheme
a.
the force exerted per unit charge;
on a positive small/test charge;
\(E = \frac{{ke}}{{{r^2}}} = \frac{{9 \times {{10}^9} \times 1.6 \times {{10}^{ – 19}}}}{{{{10}^{ – 30}}}}\);
\( = 1.4 \times {10^{21}}{\rm{N}}{{\rm{C}}^{ – 1}}\) or Vm-1;
(i) into the (plane of the) paper;
(ii) Ee=Bev or E=Bv;
=(2.3×10-4×3.9×106=)900/897;
NC-1 or Vm-1;
proton number: 8
nucleon number: 17
(both needed)
16.9991u+1.0073u-[14.0031u+4.0026u];
=-7.00×10-4;
7.000×10-4×931.5=0.6521MeV;
(∼0.7MeV)
(i) isotope:
same proton number/element/number of protons and different number of neutrons/nucleon number/neutron number; } (both needed)
half-life:
time for the activity (of a radioactive sample) to fall by half its original value / time for half the radioactive/unstable nuclei/atoms (in a sample) to decay;
(ii) 
(approximately) exponential shape;
minimum of three half lives shown;
graph correct at \(\left[ {{T_{\frac{1}{2}}},\frac{{{N_0}}}{2}} \right],\left[ {2{T_{\frac{1}{2}}},\frac{{{N_0}}}{4}} \right],\left[ {3{T_{\frac{1}{2}}},\frac{{{N_0}}}{8}} \right]\);
temperature is a measure of the (average) kinetic energy of the molecules;
at the boiling point, energy supplied (does not increase the kinetic energy) but (only) increases the potential energy of the molecules/goes into increasing the separation of the molecules/breaking one molecule from another / OWTTE;
(energy gained by cold water is) 0.300×4180×[34.6-15.2] / 24327;
(energy lost by cooling water is) 0.012×4180×[100-34.6] / 3280;
(energy lost by condensing steam is) 0.012L;
1.75×106(Jkg-1)/
\(\frac{{\left[ {{\rm{their energy gained by cold water}} – {\rm{their energy lost by cooling water}}} \right]}}{{0.012}}\);
Award [4] for 1.75×106(Jkg-1).
Award [2 max] for an answer that ignores cooling of condensed steam.
some of the energy (of the condensing steam) is lost to the surroundings;