Question
An electrically heated pad is designed to keep a pet warm.
The pad is heated using a resistor that is placed inside the pad. The dimensions of the resistor are shown on the diagram. The resistor has a resistance of \(4.2 \Omega\) and a total length of \(1.25 \mathrm{~m}\).

When there is a current in the resistor, the temperature in the pad changes from a room temperature of \(20^{\circ} \mathrm{C}\) to its operating temperature at \(35^{\circ} \mathrm{C}\).
(a) The designers state that the energy transferred by the resistor every second is \(15 \mathrm{~J}\).
Calculate the current in the resistor. [1]
(b) The designers wish to make the resistor from carbon fibre.
The graph shows the variation with temperature, in Kelvin, of the resistivity of carbon fibre.

(i) The resistor has a cross-sectional area of \(9.6 \times 10^{-6} \mathrm{~m}^2\).
Show that a resistor made from carbon fibre will be suitable for the pad. [3]
(ii) The power supply to the pad has a negligible internal resistance.
State and explain the variation in current in the resistor as the temperature of the pad increases.[2]
(c) When there is a current in the resistor, magnetic forces act between the resistor strips. For the part of the resistor labelled RS,
(i) outline the magnetic force acting on it due to the current in PQ.[1]
(ii) state and explain the net magnetic force acting on it due to the currents in \(P Q\) and \(T U\).[2]
(d) The design of the pad encloses the resistor in a material that traps air. The design also places the resistor close to the top surface of the pad.

▶️Answer/Explanation
Ans:
a.\(I=\alpha \sqrt{\frac{P}{R}}=1.9 \alpha \mathrm{A} w\)
b(i) ALTERNATIVE 1 (Calculation of length)
Read off from graph [ \(\left.2.8-3.2 \times 10^{-5} \Omega \mathrm{m}\right] \checkmark\)
Use of \(I=\frac{R A}{\rho}\)
$
I=1.3-1.4 \ll \mathrm{m} * \checkmark
$
ALTERNATIVE 2 (Calculation of area)
Read off from graph [ \(\left.2.8-3.2 \times 10^{-5} \Omega \mathrm{m}\right] \checkmark\)
Use of \(A=\rho \frac{1}{R} \checkmark\)
$
A=8.3-9.5 \times 10^{-6} \ll \mathrm{m}^2{ }^2 \checkmark
$
ALTERNATIVE 3 (Calculation of resistance)
Read off from graph [ \(\left.2.8-3.2 \times 10^{-5} \Omega \mathrm{m}\right] \checkmark\)
Use of \(R=\rho \frac{1}{A} \checkmark\)
$
R=3.6-4.2 * \Omega \approx \checkmark
$
ALTERNATIVE 4 (Calculation of resistivity)
Use of \(\rho=\frac{R A}{I} \checkmark\)
$
\rho=3.2 \times 10^{-5} \kappa \Omega \mathrm{m} \otimes \checkmark
$
Read off from graph \(260-280 \mathrm{~K} \checkmark\)
b(ii) «Resistivity and hence» resistance will decrease
«Pd across pad will not change because internal resistance is negligible» Current will increase \(\checkmark\)
c i.\&The force is» away from \(\mathrm{PQ} /\) repulsive/to the right
c ii The magnetic fields «due to currents in PQ and TU» are in opposite directions OR
There are two «repulsiven forces in opposite directions \(\checkmark\)
Net force is zero \(r\)
d. Air is a poor «thermal» conductor
Lack of convection due to air not being able to move in material
Appropriate statement about energy transfer between the pet, the resistor and surroundings
The rate of thermal energy transfer to the top surface is greater than the bottom adue to thinner material» \(\checkmark\)
This question is about magnetic fields.
A long straight vertical conductor carries an electric current. The conductor passes through a hole in a horizontal piece of paper.
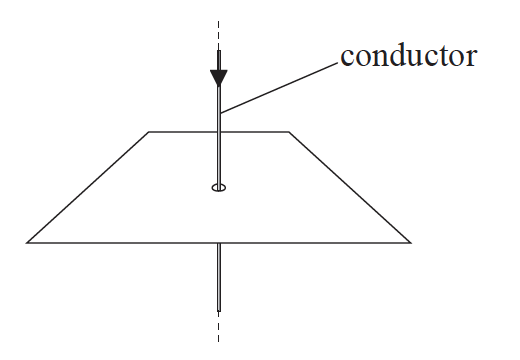
a.
State how a magnetic field arises.
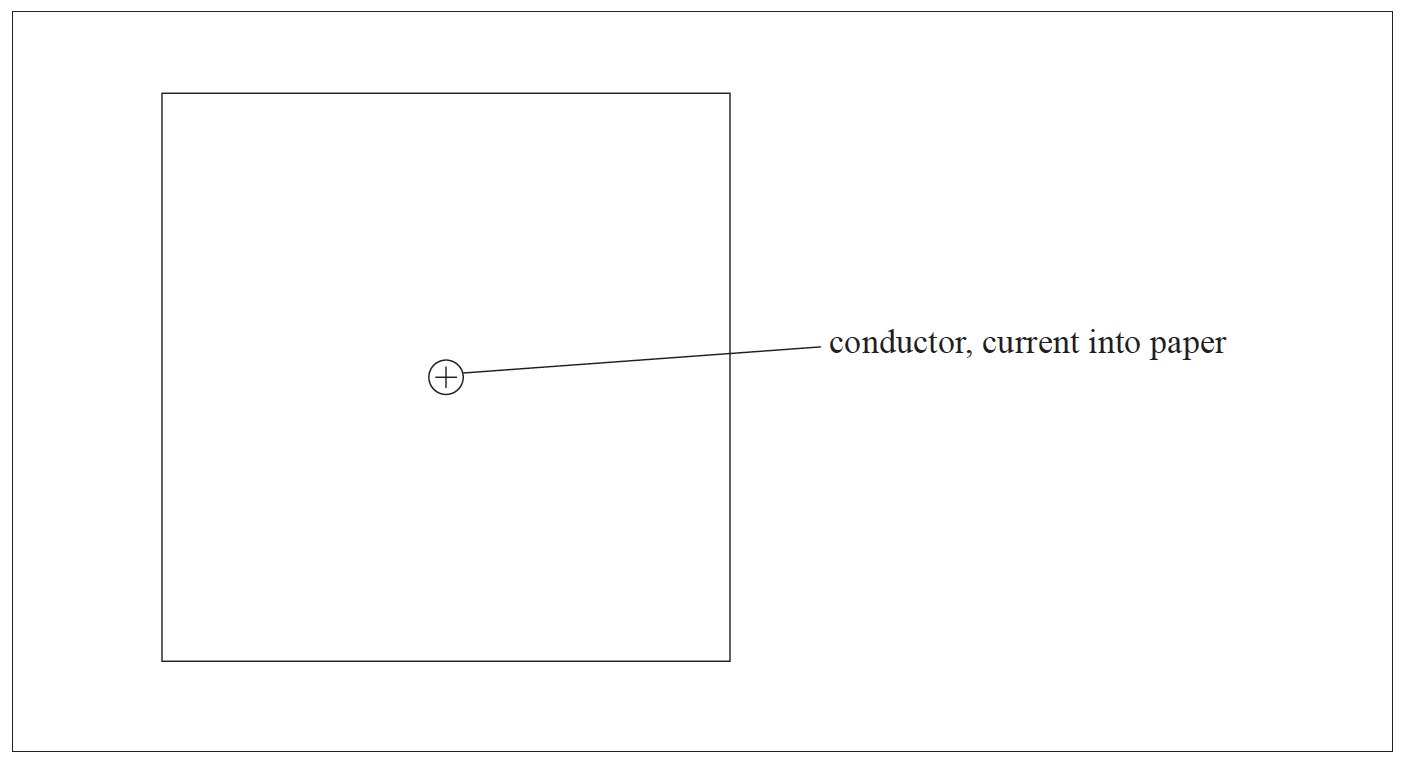
On the diagram below, sketch the magnetic field pattern around the long straight current-carrying conductor. The direction of the current is into the plane of the paper.
The long straight conductor is formed into a coil consisting of two separate turns, X and Y. The coil hangs with its axis vertical.
Assume that the turns of the coil each behave as a long straight conductor.
(i) Explain why, when there is a current in the coil, the separation of X and Y decreases.
(ii) The current in the coil is 15 A and the circumference of one turn is 0.48m. In order to restore X and Y to their original separation, a mass of 2.8×10–4 kg is suspended from turn Y. Estimate the magnetic field strength at X due to Y.
Answer/Explanation
Markscheme
a.
(electric current means) movement of charge;
Do not allow references to current alone – this is in the question.
Do not allow references to charges repelling.
at least two concentric circles;
with clockwise direction indicated;
(i) each turn subject to the magnetic field of the other / field patterns for individual turns combine;
force shown to be attractive by use of direction rule/ by consideration of field pattern / OWTTE; { (can be shown diagrammatically)
(ii) F=(0.280×10–3×9.81=)2.75×10–3N;
\(B = \frac{F}{{Il}}\) or correct substitution 2.75×10–3=B×(15)×0.48;
\(B = \left( {\frac{{2.75 \times {{10}^{ – 3}}}}{{15 \times 0.48}} = } \right)3.8 \times {10^{ – 4}}{\rm{T}}\);
Question
This question is about motion in a magnetic field.
An electron, that has been accelerated from rest by a potential difference of 250 V, enters a region of magnetic field of strength 0.12 T that is directed into the plane of the page.

a.
The electron’s path while in the region of magnetic field is a quarter circle. Show that the
(i) speed of the electron after acceleration is 9.4×106ms−1.
(ii) radius of the path is 4.5×10−4m.
The diagram below shows the momentum of the electron as it enters and leaves the region of magnetic field. The magnitude of the initial momentum and of the final momentum is 8.6×10−24Ns.

(i) On the diagram above, draw an arrow to indicate the vector representing the change in the momentum of the electron.
(ii) Show that the magnitude of the change in the momentum of the electron is 1.2×10−23Ns.
(iii) The time the electron spends in the region of magnetic field is 7.5 ×10−11s. Estimate the magnitude of the average force on the electron.
Answer/Explanation
Markscheme
a.
(i) \(v = \sqrt {\frac{{2eV}}{m}} \);
\(v = \sqrt {\frac{{2 \times 1.6 \times {{10}^{ – 19}} \times 250}}{{9.1 \times {{10}^{ – 31}}}}} \);
=9.4×106ms−1
(ii) evB=m\(\frac{{{v^2}}}{r}\);
\(r = \frac{{9.1 \times {{10}^{ – 31}} \times 9.4 \times {{10}^6}}}{{1.6 \times {{10}^{ – 19}} \times 0.12}}\);
=4.5×10−4m
(i) vector as shown;
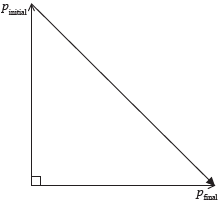
(ii) \(\Delta p = \sqrt {{{\left[ {8.6 \times {{10}^{ – 24}}} \right]}^2} + {{\left[ {8.6 \times {{10}^{ – 24}}} \right]}^2}} \);
=1.2×10−23Ns