IB myp 4-5 physics – Practice Questions- All Topics
Topic :Forces and energy- Gravity and gravitational fields
Topic :Forces and energy– Weightage : 21 %
All Questions for Topic : Forces and energy -Gravitational force, Gravitational acceleration, Newton’s law of universal gravitation, Weight , Gravitational field, Gravitational field strength
Question(11marks)
A robotic probe is sent into space to collect data from three of the four inner planets: Mercury, Mars and Venus.
While passing close by each planet the probe drops a test object from a height of 100.0 $\mathrm{m}$, the shape of the object ensures that any frictional forces are negligible over a fall of this distance.
Fly with the probe to collect the data.Below, the name of each planet to measure the time taken for the test object to fall.
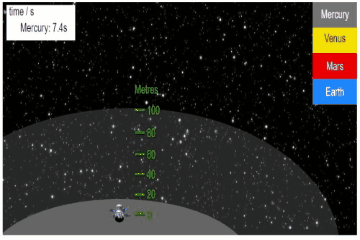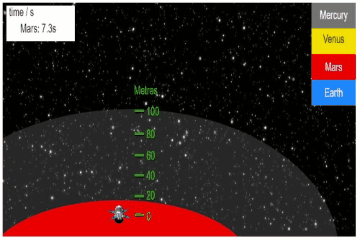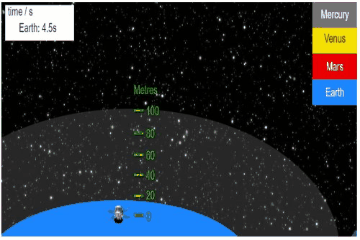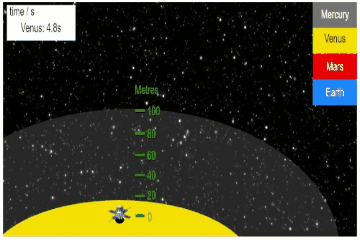
Question a (3 mark)
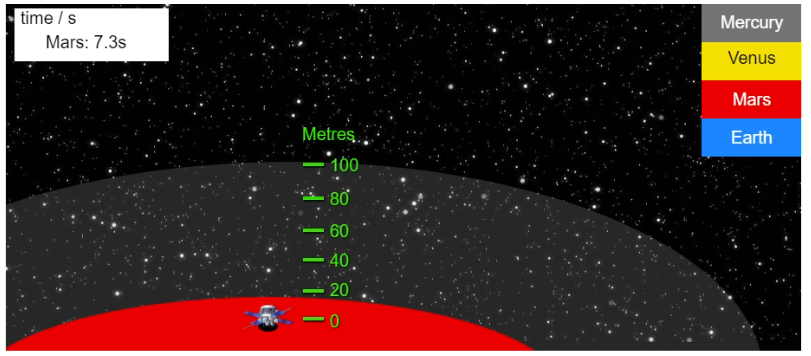
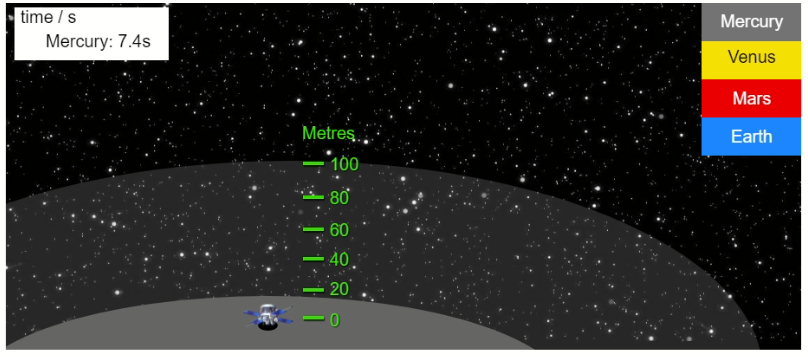
Using the data you collected above, calculate the acceleration due to gravity on Mercury and Mars.
Mercury:
Mars:
▶️Answer/Explanation
Ans:
To calculate the acceleration due to gravity on Mercury and Mars, we can use the equation for free fall:
\[d = \frac{1}{2}gt^2\]
where:
– \(d\) is the distance fallen (100.0 m in this case),
– \(g\) is the acceleration due to gravity, and
– \(t\) is the time taken for the object to fall.
For Mercury:
Distance fallen, \(d = 100.0 \, \mathrm{m}\)
Time taken, \(t = 7.4 \, \mathrm{s}\)
Using the equation above, we can rearrange it to solve for \(g\):
\[g = \frac{2d}{t^2}\]
Substituting the values for Mercury:
\[g_{\text{Mercury}} = \frac{2 \times 100.0 \, \mathrm{m}}{(7.4 \, \mathrm{s})^2}\]
Calculating \(g_{\text{Mercury}}\):
\[g_{\text{Mercury}} \approx 3.7 \, \mathrm{m/s^2}\]
For Mars:
Distance fallen, \(d = 100.0 \, \mathrm{m}\)
Time taken, \(t = 7.3 \, \mathrm{s}\)
Using the equation for \(g\) again:
\[g_{\text{Mars}} = \frac{2d}{t^2}\]
Substituting the values for Mars:
\[g_{\text{Mars}} = \frac{2 \times 100.0 \, \mathrm{m}}{(7.3 \, \mathrm{s})^2}\]
Calculating \(g_{\text{Mars}}\):
\[g_{\text{Mars}} \approx 3.5 \, \mathrm{m/s^2}\]
Therefore, the acceleration due to gravity on Mercury is approximately \(3.7 \, \mathrm{m/s^2}\) and on Mars is approximately \(3.5 \, \mathrm{m/s^2}\).
The scientists receiving the data on Earth know that gravitational field strength $(g)$ is proportional to a planet’s density $(\rho)$ and its radius $(r)$.
gravitational field strength $\sim$ density $\times$ radius
$$
g \sim \rho \times r
$$
The radius of Mercury is about two thirds of the radius of Mars.

Question b (2 mark)
Explain why Mars and Mercury can have almost the same value of $g$, if Mars has a much larger radius.
▶️Answer/Explanation
Ans:
To explain why Mars and Mercury can have almost the same value of \(g\) despite Mars having a much larger radius, we need to consider the relationship between gravitational field strength, density, and radius.
The equation \(g \sim \rho \times r\) suggests that the gravitational field strength is directly proportional to both the density (\(\rho\)) and the radius (\(r\)) of a planet. However, it is important to note that this equation assumes that the masses of the planets remain constant.
In the case of Mars and Mercury, even though Mars has a significantly larger radius, it is also less dense compared to Mercury. This means that the density of Mars (\(\rho_{\text{Mars}}\)) is relatively lower than the density of Mercury (\(\rho_{\text{Mercury}}\)). The relationship between the radius and density affects the overall value of \(g\) for each planet.
Since Mars has a larger radius but a lower density, the effect of the larger radius on the gravitational field strength is offset by the lower density. On the other hand, even though Mercury has a smaller radius, its higher density compensates for the smaller radius when calculating \(g\). As a result, the two planets can have almost the same value of \(g\) despite their differences in size.
In summary, the combination of the relationship between density and radius plays a crucial role in determining the gravitational field strength. In the case of Mars and Mercury, the larger radius of Mars is counterbalanced by its lower density, allowing the two planets to have similar values of \(g\).
Question:
Use Newton’s law of gravitation to calculate the force of gravity that would act between you and someone standing next to you. What does the size of this force say about how we notice the interaction of gravity?
▶️Answer/Explanation
Ans: Let r = 1 m (distance between centers of mass), M1 = M2 = 70 kg
\(F=\frac{6.67\times 10^{-11}\times 70\times 70}{1^{2}}=3.3\times 10^{-7}N\)
This gravitational force is very small. Generally, we do not notice the interaction of gravity unless the masses involved are very large.