IB myp 4-5 MATHEMATICS – Practice Questions- All Topics
Topic :Functions–Transformation of quadratic functions
Topic :Function- Weightage : 21 %
All Questions for Topic : Representation and shape of more complex functions,Transformation of quadratic functions,Rational functions,Graphing trigonometric functions,Linear programming, including inequalities,Networks-edges and arcs, nodes/ vertices, paths,Calculating network pathways,Weighted networks,Domain and range
Question
In this question, you will investigate areas of rhombuses.
The parabola $y=2 x^2$ is shown in the graph below. Different sized rhombuses are drawn inside the parabola.
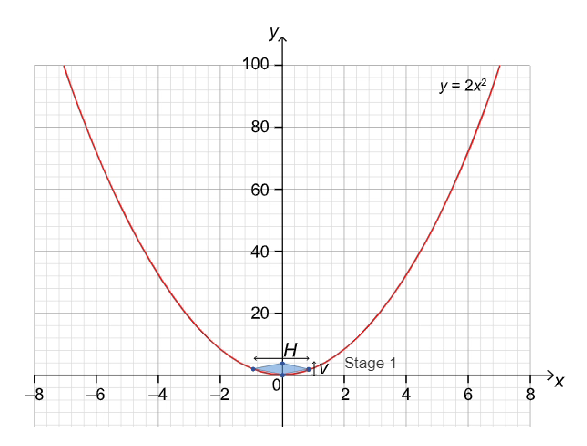 | 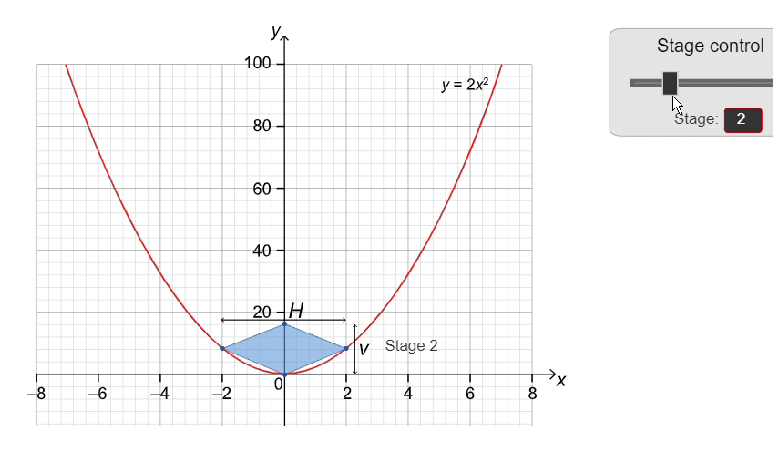 |
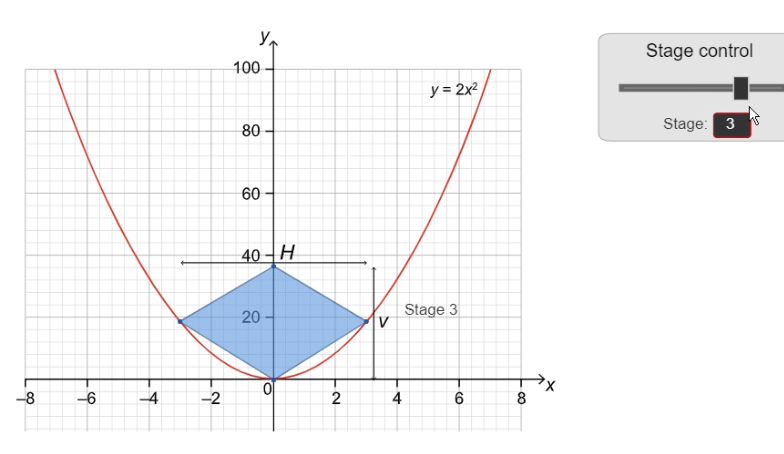 | 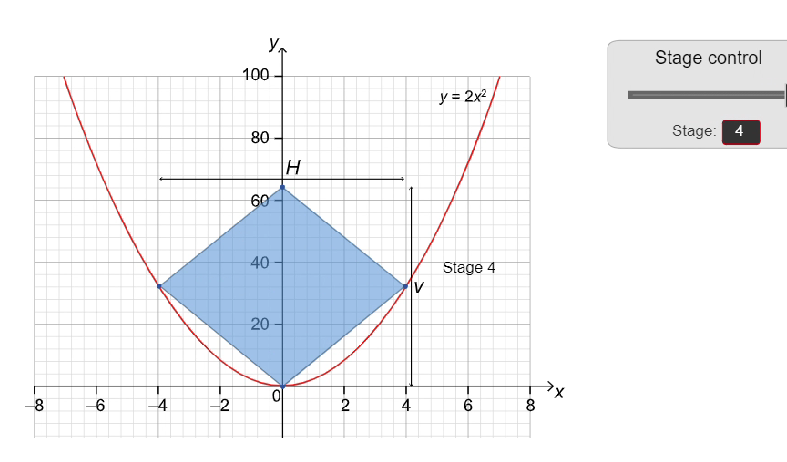 |
Question (a)
Write down the missing values in the table.

▶️Answer/Explanation
Ans:
The pattern seems to be related to the squares of consecutive odd numbers. The vertical length of the rhombus (V) for each stage (n) can be calculated using the formula:
\[ V = n^2 \times 4 \]
Here, \( n \) represents the stage number. Using this formula, we can calculate the missing values for stages 5 and 6:
For stage 5:
\[ V = 5^2 \times 4 = 100 \]
For stage 6:
\[ V = 6^2 \times 4 = 144 \]
So, the missing values for stages 5 and 6 are 100 and 144, respectively. Your completed table would look like this:

Question (b)
Describe, in words, two patterns for $V$.
▶️Answer/Explanation
Ans:
Certainly! Here are two ways to describe the patterns for the vertical length \(V\) of the rhombus in terms of the stage number \(n\):
1. **Quadratic Growth Pattern:**
The vertical length \(V\) of the rhombus follows a quadratic growth pattern. For each successive stage \(n\), the vertical length \(V\) increases as the square of the stage number. In other words, the vertical length grows quadratically with respect to the stage number. This can be described as a “stage-squared” relationship, where the value of \(V\) is obtained by multiplying the square of the stage number by a constant factor of 4.
2. **Odd Number Squares Pattern:**
Another way to describe the pattern is by focusing on the relationship between the stage number \(n\) and the nature of the numbers in the sequence. The vertical length \(V\) of the rhombus is directly related to the squares of consecutive odd numbers. As the stage number increases by 1 with each stage, the odd number corresponding to that stage is squared and then multiplied by 4 to obtain the value of \(V\). This creates a sequence of vertical lengths that corresponds to the squares of the odd numbers: 4, 16, 36, 64, 100, 144, and so on.
Question (c)
Write down a general rule for $V$ in terms of $n$.
▶️Answer/Explanation
Ans:
The relationship between the stage number \(n\) and the vertical length of the rhombus \(V\) can be expressed using the formula:
\[ V = n^2 \times 4 \]
In this formula, \(n\) represents the stage number, and \(V\) represents the vertical length of the rhombus at that stage. The formula states that the vertical length of the rhombus is equal to the square of the stage number multiplied by 4. This is based on the observed pattern that the vertical length of the rhombus increases quadratically with the stage number.