Question
A function is defined by f (x)\( = 2 – \frac{12}{x+5}\) for −7 ≤ x ≤ 7, x ≠ −5.
a. Find the range of f . [3]
b. Find an for the inverse function f −1 (x). The domain is not required. [3]
c. Write down the range of f −1 (x) . [1]
▶️Answer/Explanation
(a) ( f ( −7) =8 ) and ( f (7) 1 = 1) r
ange is f (x ) ≤ 1, f (x ) ≥ 8
(b) interchanging x, y at any stage
\(y= 2 – \frac{12}{x+5}\0
\(\frac{12}{x+5}= 2-y\)
\(\frac{12}{(2-y)}= x+5\)
\frac{12}{(2-y)}- 5=x
\((f^{-1}(x)\frac{12}{2-x}-5)\)
\(= \frac{2+5x}{2-x}\)
(c) range is -7 ≤ f-1 (x) ≤ 7, f-1 (x)≠ 5
Question
The function \(f(x) = In (\frac{1}{x-2})\) is defined for x>2, \(x\epsilon \mathbb{R}\)
(a) Find an expression for \(f^{-1}(x)\). You are not required to state a domain.
(b) Solve \(f(x)=f^{-1}(x)\).
▶️Answer/Explanation
Ans:
(a) \(y = In (\frac{1}{x-2})\)
an attempt to isolate x (or y if switched)
\(e^y = \frac{1}{x-2}\)
\(x – 2 = e^{-y}\)
\(x = e^{-y}+2\)
switching x and y (seen anywhere)
\(f^{-1}(x) = e^{-x}+2\)
(b) sketch of f(x) and \(f^{-1}(x)\)
x = 2.12 (2.12002…)
Question
The graph of y = f (x) for -4 ≤ x ≤ 6 is shown in the following diagram.
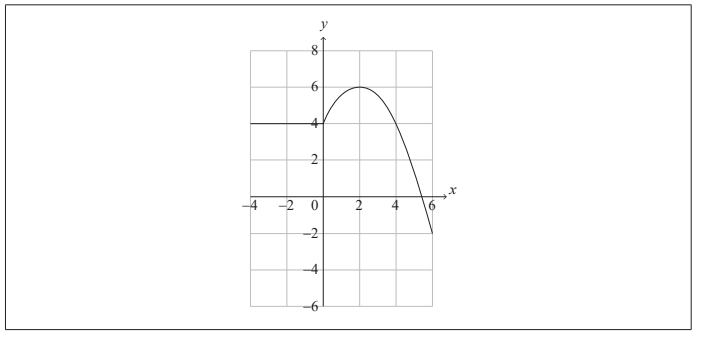
(a) Write down the value of
(i) f (2) ;
(ii) ( f o f )(2) . [2]
(b) Let g(x) = \(\frac{1}{2} f (x) +1\) for -4 ≤ x ≤ 6 . On the axes above, sketch the graph of g . [3]
▶️Answer/Explanation
Ans:
(a) (i) f(2) = 6
(ii) (fof)2=− 2 [2 marks]
(b) 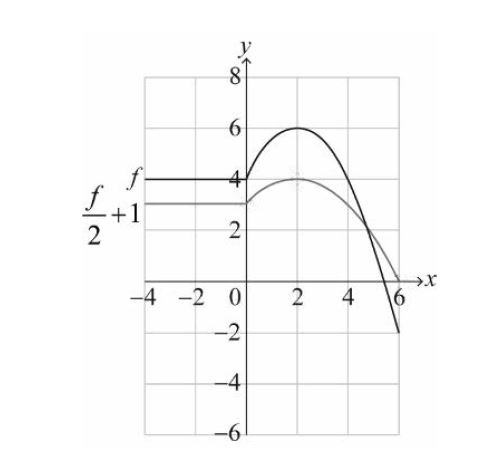
Question
The functions f and g are defined as:
\[f(x) = {{\text{e}}^{{x^2}}},{\text{ }}x \geqslant 0\]
\[g(x) = \frac{1}{{x + 3}},{\text{ }}x \ne – 3.\]
(a) Find \(h(x){\text{ where }}h(x) = g \circ f(x)\) .
(b) State the domain of \({h^{ – 1}}(x)\) .
(c) Find \({h^{ – 1}}(x)\) .
▶️Answer/Explanation
Markscheme
(a) \(h(x) = g \circ f(x) = \frac{1}{{{{\text{e}}^{{x^2}}} + 3}},{\text{ }}(x \geqslant 0)\) (M1)A1
(b) \(0 < x \leqslant \frac{1}{4}\) A1A1
Note: Award A1 for limits and A1 for correct inequality signs.
(c) \(y = \frac{1}{{{{\text{e}}^{{x^2}}} + 3}}\)
\(y{{\text{e}}^{{x^2}}} + 3y = 1\) M1
\({{\text{e}}^{{x^2}}} = \frac{{1 – 3y}}{y}\) A1
\({x^2} = \ln \frac{{1 – 3y}}{y}\) M1
\(x = \pm \sqrt {\ln \frac{{1 – 3y}}{y}} \)
\( \Rightarrow {h^{ – 1}}(x) = \sqrt {\ln \frac{{1 – 3x}}{x}} {\text{ }}\left( { = \sqrt {\ln \left( {\frac{1}{x} – 3} \right)} } \right)\) A1
[8 marks]
Question
Let \(f(x) = \frac{4}{{x + 2}},{\text{ }}x \ne – 2{\text{ and }}g(x) = x – 1\).
If \(h = g \circ f\) , find
(a) h(x) ;
(b) \({h^{ – 1}}(x)\) , where \({h^{ – 1}}\) is the inverse of h.
▶️Answer/Explanation
Markscheme
(a) \(h(x) = g\left( {\frac{4}{{x + 2}}} \right)\) (M1)
\( = \frac{4}{{x + 2}} – 1\,\,\,\,\,\left( { = \frac{{2 – x}}{{2 + x}}} \right)\) A1
(b) METHOD 1
\(x = \frac{4}{{y + 2}} – 1\,\,\,\,\,\)(interchanging x and y) M1
Attempting to solve for y M1
\((y + 2)(x + 1) = 4\,\,\,\,\,\left( {y + 2 = \frac{4}{{x + 1}}} \right)\) (A1)
\({h^{ – 1}}(x) = \frac{4}{{x + 1}} – 2\,\,\,\,\,(x \ne – 1)\) A1 N1
METHOD 2
\(x = \frac{{2 – y}}{{2 + y}}\,\,\,\,\,\)(interchanging x and y) M1
Attempting to solve for y M1
\(xy + y = 2 – 2x\,\,\,\,\,\left( {y(x + 1) = 2(1 – x)} \right)\) (A1)
\({h^{ – 1}}(x) = \frac{{2(1 – x)}}{{x + 1}}\,\,\,\,\,(x \ne – 1)\) A1 N1
Note: In either METHOD 1 or METHOD 2 rearranging first and interchanging afterwards is equally acceptable.
[6 marks]
