Question 13. [Maximum mark: 7]
A submarine is located in a sea at coordinates (0.8, 1.3, −0.3) relative to a ship positioned at the origin O. The x direction is due east, the y direction is due north and the z direction is vertically upwards.
All distances are measured in kilometres.
The submarine travels with direction vector 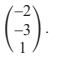
( a ) Assuming the submarine travels in a straight line, write down an equation for the line
along which it travels. [2]
b (i) Find the coordinates of P.
(ii) Find OP. [5]
▶️Answer/Explanation
(a) r = 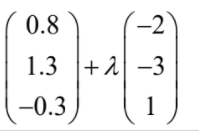 (b) (i) 0.3 + λ = 0 ⇒ λ = 0.3
(b) (i) 0.3 + λ = 0 ⇒ λ = 0.3 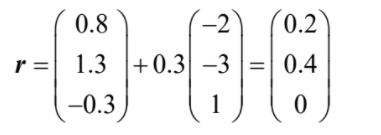 P has coordinates (0.2, 0.4, 0) (ii) \(\sqrt{0.2^{2}+ 0.4^{2}}= 0.447 km (=447m)\)
P has coordinates (0.2, 0.4, 0) (ii) \(\sqrt{0.2^{2}+ 0.4^{2}}= 0.447 km (=447m)\)
Question
. The position vector of a particle, P, relative to a fixed origin O at time t is given by
\(\overrightarrow{OP} = \binom{sin(t^2)}{cos(t^2)}\).
(a) Find the velocity vector of P.
(b) Show that the acceleration vector of P is never parallel to the position vector of P.
▶️Answer/Explanation
Ans:
(a) attempt at chain rule
\(\begin{pmatrix}
v=\frac{dOP}{dt}
\end{pmatrix}\begin{pmatrix}
2t cos t^2\\
-2t sin t^2
\end{pmatrix}\)
(b) attempt at product rule
\(a=\begin{pmatrix}
2 cos t^2 – 4t^2 sin t^2\\
-2 sin t^2 – 4t^2 cos t^2
\end{pmatrix}\)
METHOD 1
let \(S= sin t^2\) and \(C = cos t^2\)
finding cos \(\theta \) using
\(a. \overrightarrow{OP} = 2SC – 4t^2 S^2 – 2SC – 4t^2C^2 = – 4t^2\)
\(|\overrightarrow{OP}| = 1\)
\(|a| = \sqrt{(2C-4t^2S)^2 + (-2S – 4t^2 C)^2}\)
\(=\sqrt{4 + 16t^4}> 4t^2\)
it \(\theta\) is the angle between them, then
\(cos \theta = -\frac{4t^2}{\sqrt{4+16t^4}}\)
so -1 < cos \(\theta\) < 0 therefore the vectors are never parallel
METHOD 2
solve
\(\begin{pmatrix}
2cos t^2 – 4t^2 sin t^2\\ -2 sin t^2 – 4t^2 cos t^2
\end{pmatrix} = k \binom{sin t^2}{cos t^2}\)
then
\((k=) \frac{2cos t^2 – 4t^2 sin t^2}{sin t^2} = \frac{-2 sin t^2 – 4t^2 cos t^2}{cos t^2}\)
\(2cos^2 t^2 – 4t^2 cos t^2 sin t^2 = -2 sin^2 t^2 – 4t^2 cos t^2 sin t^2\)
\(2cos^2 t^2 + 2 sin^2 t^2 =0\)
2 = 0
this is never true so the two vectors are never parallel
MEHTOD 3
embedding vectors in a 3d space and taking the cross product.
\(\begin{pmatrix}
sin t^2\\ cos t^2
\\ 0
\end{pmatrix} \times \begin{pmatrix}
2 cos t^2-4t^2 sin t^2\\-2 sin t^2 – 4t^2 cos t^2
\\ 0
\end{pmatrix} = \begin{pmatrix}
0\\0
\\ -2sin^2t^2 – 4t^2 cos t^2 sin t^2 – 2 cos^2 t^2 + 4t^2 cos t^2 sin t^2
\end{pmatrix}\)
\(=\begin{pmatrix}
0\\0
\\ -2
\end{pmatrix}\)
since the cross product is never zero, the two vectors are never parallel
[MAI 3.15] VECTORS AND KINEMATICS-manav
Question
[Maximum mark: 9]
The motion of a particle is given by the equation \(\vec{r}=\left(\begin{array}{l}3 \\ 5\end{array}\right)+t\left(\begin{array}{l}4 \\ 3\end{array}\right)\) where t is in seconds.
(a) Find the initial position of the particle and its position after 2 seconds. [2]
(b) Find the velocity and the speed of the particle. [3]
(c) How far from the origin is the particle after 2 seconds? [2]
(d) How far from its initial position is the particle after 2 seconds? [2]
▶️Answer/Explanation
Ans:
(a) (3,5) and (11,11)
(b) velocity \(v=\left(\begin{array}{l}4 \\ 3\end{array}\right)\), speed \(|v|=5\)
(c) \(11 \sqrt{2}\)
(d) 10
Question
[Maximum mark: 6]
A particle is initially at point A(2,3). Complete the following table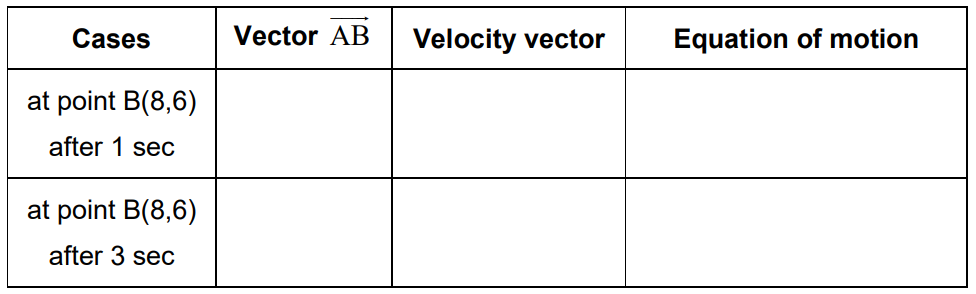
▶️Answer/Explanation
Ans: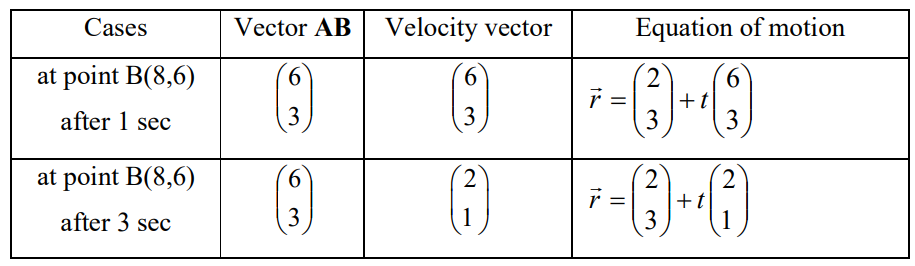
Question
[Maximum mark: 7]
Two bodies are moving according to the equations
\(\boldsymbol{r}_{1}=\left(\begin{array}{l}1 \\ 4 \\ 3\end{array}\right)+t\left(\begin{array}{l}2 \\ 1 \\ 2\end{array}\right)\) and \(\boldsymbol{r}_{2}=\left(\begin{array}{l}4 \\ 4 \\ 5\end{array}\right)+t\left(\begin{array}{l}1 \\ 2 \\ 2\end{array}\right)\)
(a) Write down the velocity vectors and find the speeds of the two bodies. [4]
(b) Show that P(5,6,7) is a common point of their paths. [2]
(c) Do the two bodies collide or not? [1]
▶️Answer/Explanation
Ans:
(a) \(v_{1}=\left(\begin{array}{l}2 \\ 1 \\ 2\end{array}\right), v_{2}=\left(\begin{array}{l}1 \\ 2 \\ 2\end{array}\right)\) speeds: \(\left|v_{1}\right|=\sqrt{9}=3,\left|v_{2}\right|=\sqrt{9}=3\)
(b) (5,6,7) satisfies r1 for t = 2 and r2 for t = 1.
(c) They do not collide since at the point of intersection \(t_{1} \neq t_{2}\)
