Question 8. [Maximum mark: 7]
Two lines L1 and L2 are given by the following equations, where p∈R.
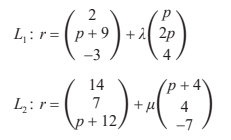
It is known that L1 and L2 are perpendicular.
a.Find the possible value(s) for p . [3]
b. In the case that p < 0 , determine whether the lines intersect. [4]
▶️Answer/Explanation
(a) setting a dot product of the direction vectors equal to zero 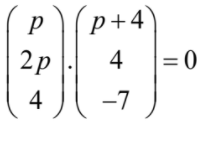
\(p(p+4)+8p – 28 = 0\)
\(p2+ 12 p +28 = 0\)
\((p + 14) (p -2 ) = 0\)
\(p =-14\) ,\( p = 2 \)
(b) p =−14 ⇒ 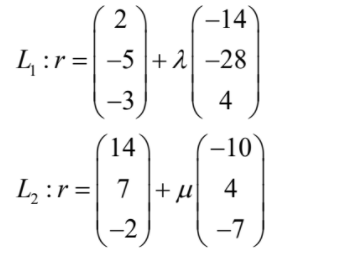
a common point would satisfy the equations
2 – 14λ = 14 -10μ …………(i)
−5−28λ = 7+ 4μ …………….(ii)
-3+ 4λ = -2-7μ ………….(iii)
METHOD 1
solving the first two equations simultaneously
\(\lambda = – \frac{1}{2}\)
\(\mu =\frac{1}{2}\)
substitute into the third equation: \(-3+ 4(-\frac{1}{2})\) ≠ \(-2+\frac{1}{2}(-7)\) so lines do not intersect.
METHOD 2 attempting to solve the equations using a GDC
GDC indicates no solution so lines do not intersect
Question 13. [Maximum mark: 7]
A submarine is located in a sea at coordinates (0.8, 1.3, −0.3) relative to a ship positioned at the origin O. The x direction is due east, the y direction is due north and the z direction is vertically upwards.
All distances are measured in kilometres.
The submarine travels with direction vector 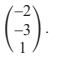
( a ) Assuming the submarine travels in a straight line, write down an equation for the line
along which it travels. [2]
b (i) Find the coordinates of P.
(ii) Find OP. [5]
▶️Answer/Explanation
(a) r = 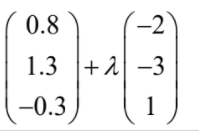 (b) (i) 0.3 + λ = 0 ⇒ λ = 0.3
(b) (i) 0.3 + λ = 0 ⇒ λ = 0.3 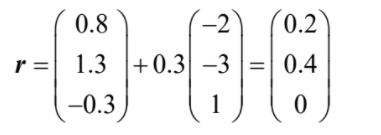 P has coordinates (0.2, 0.4, 0) (ii) \(\sqrt{0.2^{2}+ 0.4^{2}}= 0.447 km (=447m)\)
P has coordinates (0.2, 0.4, 0) (ii) \(\sqrt{0.2^{2}+ 0.4^{2}}= 0.447 km (=447m)\)
Question
The equation of the line y = mx + c can be expressed in vector form r = a + \(\lambda b\).
(a) Find the vectors a and b in terms of m and/or c.
The matrix M is defined by \(\begin{pmatrix}
6 &3 \\
4& 2
\end{pmatrix}\)
(b) Find the value of det M.
The line y = mx + c (where \(m \neq – 2)\) is transformed into a new line using the transformation described by matrix M.
(c) Show that the equation of the resulting line does not depend on m or c.
▶️Answer/Explanation
Ans:
(a) (one vector to the line is \(\binom{1}{m}\) therefore) a= (\(\binom{0}{c} \)
the line goes m up for every 1 across
(so the direction vector is) \(b= ( \binom{1}{m}\)
(b) (from GDC OR \(6 \times 2 – 4 \times 3) \) |M| = 0
(c) METHOD 1
\(\binom{X}{Y} = \begin{pmatrix}
6 & 3\\
4 & 2
\end{pmatrix} \binom{x}{mx+c}= \binom{6x + 3mx + 3c}{4x + 2mx + 2c}\)
therefore the new line has equation 3Y = 2X
which is independent of m or c
METHOD 2
take two points on the line, e.g. (0, c) and (1, m+c)
these map to \(\begin{pmatrix}
6 & 3\\
4 & 2
\end{pmatrix}\binom{0}{c}=\binom{3c}{2c}\)
and \(\begin{pmatrix}
6 & 3\\
4 & 2
\end{pmatrix}\binom{1}{m+c}=\binom{6+3m+3c}{4+2m+2c}\)
therefore a direction vector is \(\binom{6+3m}{4+2m}=(2+m)\binom{3}{2}\)
(since \(\neq -2\)) a direction vector is \(\binom{3}{2}\)
the line passes through \(\binom{3c}{2c})-c \biniom{3}{2} = \binom{0}{0}\) therefore it always has the
origin as a jump-on vector
the vector equation is therefore \(r=\mu \binom{3}{2}\)
which is independent of m or c
METHOD 3
\(r=\begin{pmatrix}
6 & 3\\
4 & 2
\end{pmatrix}(\binom{0}{c}+ \lambda \binom{1}{m})=\binom{3c}{2c}+ \lambda \binom{6+3m}{4+2m}\)
\(=c \binom{3}{2}+(2+m)\lambda \binom{3}{2}\)
\(=\mu \binom{3}{2}\)
where \(\mu=c+(2+m) \lambda\) is an arbitrary parameter.
which is independent of m or c (as \(\mu\) can take any value)
Question
Points A and B have coordinates (1, 1, 2) and (9, m, -6) respectively.
Express AB in terms of m . [2]
The line L , which passes through B, has equation r
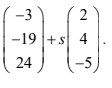
Find the value of m . [5]
Consider a unit vector u , such that \(\mathbf{u}=pi-\frac{2}{3}j+\frac{1}{3}k\) , where p > 0 .
Point C is such that BC = 9u .
Find the coordinates of C. [8]
▶️Answer/Explanation
Ans:
- (a)
- valid approach to find \(\overrightarrow{AB}\)
- eg \(\overrightarrow{OB}-\overrightarrow{OA}\) , A – B
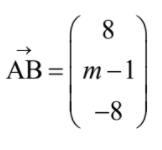
- (b)
- valid approach
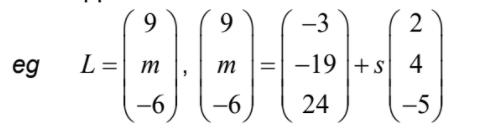
- one correct equation eg − 3 + 2s = 9, -6 = 24 -5s
- correct value for s eg s = 6
- substituting their s value into their expression/equation to find m
- eg -19 + 6 × 4
- m = 5
- valid approach
- (c)
- valid approach
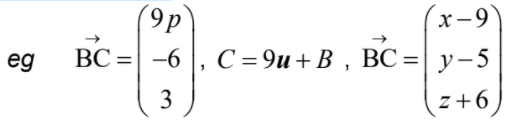
- correct working to find C
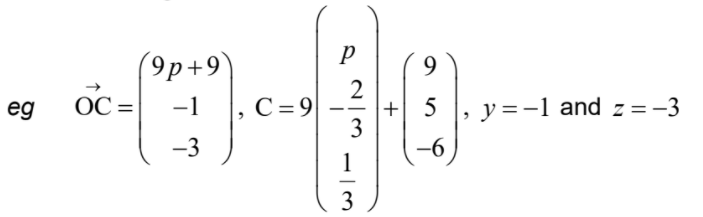
- correct approach to find u (seen anywhere)
- eg \(p^{2}+(-\frac{2}{3})^{2}+(\frac{1}{3})^{2}, \sqrt{p^{2}+\frac{4}{9}+\frac{1}{9}}\)
- recognizing unit vector has magnitude of 1
- eg |u| = 1, \(\sqrt{p^{2}+(-\frac{2}{3})^{2}+(\frac{1}{3}^{2}))}= 1, p^{2} + \frac{5}{9}\)= 1
- correct working
- eg \(p^{2} = \frac{4}{9}, p= \pm \frac{2}{3}\)
- \(p = \frac{2}{3}\)
- substituting their value of p
- eg
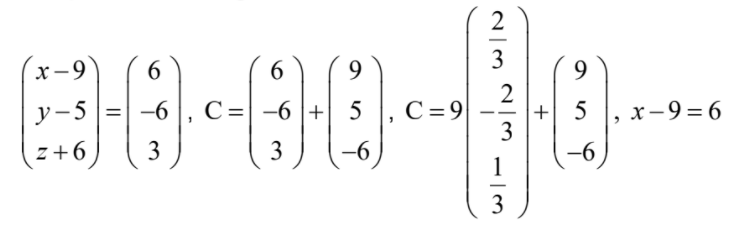

Question
Consider the line L1defined by the Cartesian equation \(\frac{x+1}{2}\) = y = 3 – z .
(a) (i) Show that the point (-1, 0, 3) lies on L1 .
(ii) Find a vector equation of L1 . [4]
Consider a second line L2 defined by the vector equation r =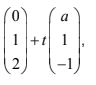 where t ∈ \(\mathbb{R}\) and a ∈ \(\mathbb{R}\).
where t ∈ \(\mathbb{R}\) and a ∈ \(\mathbb{R}\).
(b) Find the possible values of a when the acute angle between L1 and L2 is 45°. [8]
It is given that the lines L1 and L2 have a unique point of intersection, A, when a ¹ k .
(c) Find the value of k , and find the coordinates of the point A in terms of a . [7]
▶️Answer/Explanation
Ans:




