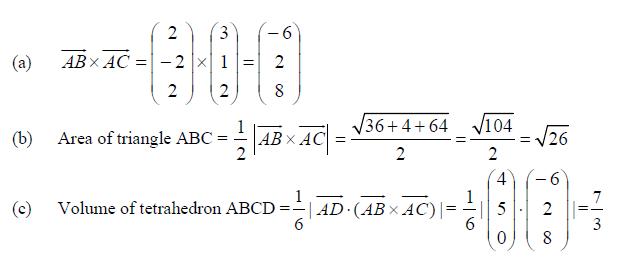Question 5. [Maximum mark: 6]
A garden has a triangular sunshade suspended from three points A(2, 0, 2), B(8, 0, 2) and C(5, 4, 3),
relative to an origin in the corner of the garden. All distances are measured in metres
a (i) Find ⟶CA .
(ii) Find ⟶CB . [2]
(b)Find ⟶CA × ⟶CB . [2]
(c)Hence find the area of the triangle ABC. [2]
▶️Answer/Explanation
(a) (i)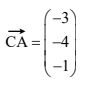 
(ii) 
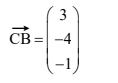(b)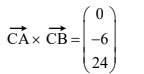 
Note: Do not award (M1) if less than 2 entries are correct. (c) area is \(\frac{1}{2}\sqrt{6^{2}+24^{2} }\) = 12.4 m2
Question
A vertical pole stands on a sloped platform. The bottom of the pole is used as the origin, O, of
a coordinate system in which the top, F, of the pole has coordinates (0 , 0 , 5.8). All units are
in metres.
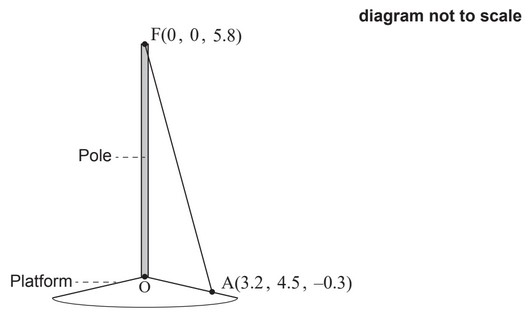
The pole is held in place by ropes attached at F.
One of these ropes is attached to the platform at point A(3.2, 4.5, −0.3). The rope forms a
straight line from A to F.
(a) Find \(\overrightarrow{AF}\)
(b) Find the length of the rope.
(c) Find \(F \widehat{A} O\), the angle the rope makes with the platform.
▶️Answer/Explanation
Ans:
Question
In the diagram below, [AB] is a diameter of the circle with centre O. Point C is on the circumference of the circle. Let \(\overrightarrow {{\text{OB}}} = \boldsymbol{b} \) and \(\overrightarrow {{\text{OC}}} = \boldsymbol{c}\) .
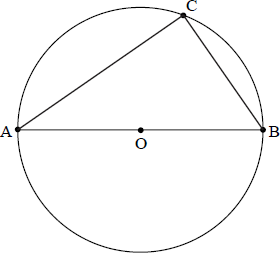
a.Find an expression for \(\overrightarrow {{\text{CB}}} \) and for \(\overrightarrow {{\text{AC}}} \) in terms of \(\boldsymbol{b}\) and \(\boldsymbol{c}\) .[2]
b.Hence prove that \({\rm{A\hat CB}}\) is a right angle.[3]
▶️Answer/Explanation
Markscheme
\(\overrightarrow {{\text{CB}}} = \boldsymbol{b} – \boldsymbol{c}\) , \(\overrightarrow {{\text{AC}}} = \boldsymbol{b} + \boldsymbol{c}\) A1A1
Note: Condone absence of vector notation in (a).
[2 marks]
\(\overrightarrow {{\text{AC}}} \cdot \overrightarrow {{\text{CB}}} = \)(b + c)\( \cdot \)(b – c) M1
= \(|\)b\({|^2}\) – \(|\)c\({|^2}\) A1
= 0 since \(|\)b\(|\) = \(|\)c\(|\) R1
Note: Only award the A1 and R1 if working indicates that they understand that they are working with vectors.
so \(\overrightarrow {{\text{AC}}} \) is perpendicular to \(\overrightarrow {{\text{CB}}} \) i.e. \({\rm{A\hat CB}}\) is a right angle AG
[3 marks]
Examiners report
Most candidates were able to find the expressions for the two vectors although a number were not able to do this. Most then tried to use Pythagoras’ theorem and confused scalars and vectors. There were few correct responses to the second part. Candidates did not seem to be able to use the algebra of vectors comfortably.
Most candidates were able to find the expressions for the two vectors although a number were not able to do this. Most then tried to use Pythagoras’ theorem and confused scalars and vectors. There were few correct responses to the second part. Candidates did not seem to be able to use the algebra of vectors comfortably.
[MAI 3.14] CROSS PRODUCT-lala
Question
[Maximum mark: 8]
Let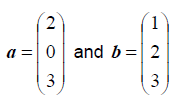 
(a) Find a · b and b · a .
(b) Find a x b and b x a .
(c) Show that a x b is perpendicular to both a and b .
▶️Answer/Explanation
Ans.
(a) a · b = b · a = 2 + 0 + 9 = 11.
(b)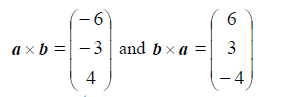 
(c) (a x b) · a = – 12 + 0 + 12 = 0, (a x b) · b = – 6 – 6 + 12 = 0
Question
[Maximum mark: 8]
Consider the points A(1,2,3), B(3,0,5), C(4,3,5)).
(a) Find \(\vec{AB}\) x \(\vec{AC}\)
(b) Find the area of the triangle ABC.
The point D(5,7,3) does not lie in the same plane with the triangle ABC.
The volume of the tetrahedron ABCD is given by \(V=\frac{1}{6}\left | \vec{AD} \cdot (\vec{AB}x\vec{AC})\right |\).
(c) Find the volume V.
▶️Answer/Explanation
Ans.
