Question
The position vector of a particle, P, relative to a fixed origin O at time t is given by
\(\overrightarrow{OP} = \binom{sin(t^2)}{cos(t^2)}\).
(a) Find the velocity vector of P.
(b) Show that the acceleration vector of P is never parallel to the position vector of P.
▶️Answer/Explanation
Ans:
(a) attempt at chain rule
\(\begin{pmatrix}
v=\frac{dOP}{dt}
\end{pmatrix}\begin{pmatrix}
2t cos t^2\\
-2t sin t^2
\end{pmatrix}\)
(b) attempt at product rule
\(a=\begin{pmatrix}
2 cos t^2 – 4t^2 sin t^2\\
-2 sin t^2 – 4t^2 cos t^2
\end{pmatrix}\)
METHOD 1
let \(S= sin t^2\) and \(C = cos t^2\)
finding cos \(\theta \) using
\(a. \overrightarrow{OP} = 2SC – 4t^2 S^2 – 2SC – 4t^2C^2 = – 4t^2\)
\(|\overrightarrow{OP}| = 1\)
\(|a| = \sqrt{(2C-4t^2S)^2 + (-2S – 4t^2 C)^2}\)
\(=\sqrt{4 + 16t^4}> 4t^2\)
it \(\theta\) is the angle between them, then
\(cos \theta = -\frac{4t^2}{\sqrt{4+16t^4}}\)
so -1 < cos \(\theta\) < 0 therefore the vectors are never parallel
METHOD 2
solve
\(\begin{pmatrix}
2cos t^2 – 4t^2 sin t^2\\ -2 sin t^2 – 4t^2 cos t^2
\end{pmatrix} = k \binom{sin t^2}{cos t^2}\)
then
\((k=) \frac{2cos t^2 – 4t^2 sin t^2}{sin t^2} = \frac{-2 sin t^2 – 4t^2 cos t^2}{cos t^2}\)
\(2cos^2 t^2 – 4t^2 cos t^2 sin t^2 = -2 sin^2 t^2 – 4t^2 cos t^2 sin t^2\)
\(2cos^2 t^2 + 2 sin^2 t^2 =0\)
2 = 0
this is never true so the two vectors are never parallel
MEHTOD 3
embedding vectors in a 3d space and taking the cross product.
\(\begin{pmatrix}
sin t^2\\ cos t^2
\\ 0
\end{pmatrix} \times \begin{pmatrix}
2 cos t^2-4t^2 sin t^2\\-2 sin t^2 – 4t^2 cos t^2
\\ 0
\end{pmatrix} = \begin{pmatrix}
0\\0
\\ -2sin^2t^2 – 4t^2 cos t^2 sin t^2 – 2 cos^2 t^2 + 4t^2 cos t^2 sin t^2
\end{pmatrix}\)
\(=\begin{pmatrix}
0\\0
\\ -2
\end{pmatrix}\)
since the cross product is never zero, the two vectors are never parallel
Question
At 1:00 pm a ship is 1km east and 4km north of a harbour. A coordinate system is defined
with the harbour at the origin. The position vector of the ship at 1:00 pm is given by \(\binom{1}{4}\)
The ship has a constant velocity of \(\binom{1.2}{-0.6})\) kilometres per hour \((km h^{-1}\).
(a) Write down an expression for the position vector r of the ship, t hours after 1:00 pm.
(b) Find the time at which the bearing of the ship from the harbour is 045 ̊.
▶️Answer/Explanation
Ans:
(a) \((r=) \binom{1}{4} + t \binom{1.2}{-0.6}\)
(b) when the bearing from the port is 045 ̊, the distance east from the port
is equal to the distance north from the port
1 + 1.2t = 4 – 0.6t
1.8t = 3
\(t = \frac{5}{3}\) (1.6666…, 1 hour 40 minutes )
time is 2:40 pm (14:40)
Question
6. A vertical pole stands on a sloped platform. The bottom of the pole is used as the origin, O, of
a coordinate system in which the top, F, of the pole has coordinates (0 , 0 , 5.8). All units are
in metres.
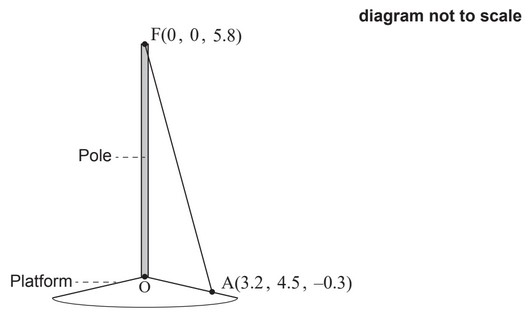
The pole is held in place by ropes attached at F.
One of these ropes is attached to the platform at point A(3.2, 4.5, −0.3). The rope forms a
straight line from A to F.
(a) Find \(\overrightarrow{AF}\)
(b) Find the length of the rope.
(c) Find \(F \widehat{A} O\), the angle the rope makes with the platform.
▶️Answer/Explanation
Ans:

Question
a.Consider the vectors a = 6i + 3j + 2k, b = −3j + 4k.
(i) Find the cosine of the angle between vectors a and b.
(ii) Find a \( \times \) b.
(iii) Hence find the Cartesian equation of the plane \(\prod \) containing the vectors a and b and passing through the point (1, 1, −1).
(iv) The plane \(\prod \) intersects the x-y plane in the line l. Find the area of the finite triangular region enclosed by l, the x-axis and the y-axis.[11]
b.Given two vectors p and q,
(i) show that p\( \cdot \)p = \(|\)p\({|^2}\);
(ii) hence, or otherwise, show that \(|\)p + q\({|^2}\) = \(|\)p\({|^2}\) + 2p\( \cdot \)q + \(|\)q\({|^2}\);
(iii) deduce that \(|\)p + q\(|\) ≤ \(|\)p\(|\) + \(|\)q\(|\).[8]
▶️Answer/Explanation
Markscheme
(i) use of a\( \cdot \)b = \(|\)a\(|\)\(|\)b\(|\cos \theta \) (M1)
a\( \cdot \)b = –1 (A1)
\(|\)a\(|\) = 7, \(|\)b\(|\) = 5 (A1)
\(\cos \theta = – \frac{1}{{35}}\) A1
(ii) the required cross product is
\(\left| {\begin{array}{*{20}{c}}
i&j&k \\
6&3&2 \\
0&{ – 3}&4
\end{array}} \right| = \) 18i – 24j -18k M1A1
(iii) using r\( \cdot \)n = p\( \cdot \)n the equation of the plane is (M1)
\(18x – 24y – 18z = 12\,\,\,\,\,(3x – 4y – 3z = 2)\) A1
(iv) recognizing that z = 0 (M1)
x-intercept \( = \frac{2}{3}\), y-intercept \( = – \frac{1}{2}\) (A1)
area \( = \left( {\frac{2}{3}} \right)\left( {\frac{1}{2}} \right)\left( {\frac{1}{2}} \right) = \frac{1}{6}\) A1
[11 marks]
(i) p\( \cdot \)p = \(|\)p\(|\)\(|\)p\(|\cos 0\) M1A1
= \(|\)p\({|^2}\) AG
(ii) consider the LHS, and use of result from part (i)
\(|\)p + q\({|^2}\) = (p + q)\( \cdot \)(p + q) M1
= p\( \cdot \)p + p\( \cdot \)q + q\( \cdot \)p + q\( \cdot \)q (A1)
= p\( \cdot \)p + 2p\( \cdot \)q + q\( \cdot \)q A1
= \(|\)p\({|^2}\) + 2p\( \cdot \)q + \(|\)q\({|^2}\) AG
(iii) EITHER
use of p\( \cdot \)q \( \leqslant \) \(|\)p\(|\)\(|\)q\(|\) M1
so 0 \( \leqslant \) \(|\)p + q\({|^2}\) = \(|\)p\({|^2}\) + 2p\( \cdot \)q + \(|\)q\({|^2}\) \( \leqslant \) \(|\)p\({|^2}\) + 2 \(|\)p\(|\)\(|\)q\(|\) + \(|\)q\({|^2}\) A1
take square root (of these positive quantities) to establish A1
\(|\)p + q\(|\) \( \leqslant \) \(|\)p\(|\) + \(|\)q\(|\) AG
OR
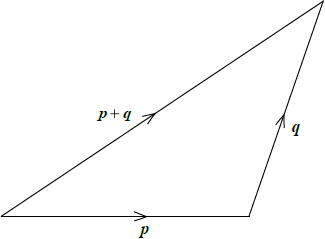 M1M1
M1M1
Note: Award M1 for correct diagram and M1 for correct labelling of vectors including arrows.
since the sum of any two sides of a triangle is greater than the third side,
\(|\)p\(|\) + \(|\)q\(|\) > \(|\)p + q\(|\) A1
when p and q are collinear \(|\)p\(|\) + \(|\)q\(|\) = \(|\)p + q\(|\)
\( \Rightarrow |\)p + q\(|\) \( \leqslant \) \(|\)p\(|\) + \(|\)q\(|\) AG
[8 marks]
Examiners report
This was the most accessible question in section B for the candidates. The majority of candidates produced partially correct answers to part (a), with nearly all candidates being able to use the scalar and vector product. Candidates found part (iv) harder and often did not appreciate the significance of letting z = 0. Candidates clearly found part (b) harder and again this was a point where candidates lost time. Many candidates attempted this using components, which was fine in part (i), fine, but time consuming in part (ii), and extremely complicated in part (iii). A number of candidates lost marks because they were careless in showing their working in part (ii) which required them to “show that”.
This was the most accessible question in section B for the candidates. The majority of candidates produced partially correct answers to part (a), with nearly all candidates being able to use the scalar and vector product. Candidates found part (iv) harder and often did not appreciate the significance of letting z = 0. Candidates clearly found part (b) harder and again this was a point where candidates lost time. Many candidates attempted this using components, which was fine in part (i), fine, but time consuming in part (ii), and extremely complicated in part (iii). A number of candidates lost marks because they were careless in showing their working in part (ii) which required them to “show that”.
Question
The diagram below shows a circle with centre O. The points A, B, C lie on the circumference of the circle and [AC] is a diameter.
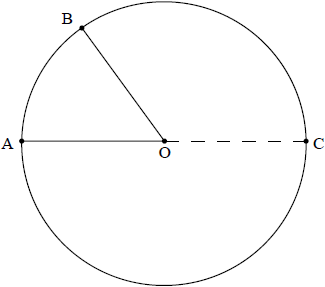
Let \(\overrightarrow {{\text{OA}}} = {\boldsymbol{a}}\) and \(\overrightarrow {{\text{OB}}} = {\boldsymbol{b}}\) .
a.Write down expressions for \(\overrightarrow {{\text{AB}}} \) and \(\overrightarrow {{\text{CB}}} \) in terms of the vectors \({\boldsymbol{a}}\) and \({\boldsymbol{b}}\) .[2]
b.Hence prove that angle \({\text{A}}\hat {\rm{B}}{\text{C}}\) is a right angle.[3]
▶️Answer/Explanation
Markscheme
\(\overrightarrow {{\text{AB}}} = {\boldsymbol{b}} – {\boldsymbol{a}}\) A1
\(\overrightarrow {{\text{CB}}} = {\boldsymbol{a}} + {\boldsymbol{b}}\) A1
[2 marks]
\(\overrightarrow {{\text{AB}}} \cdot \overrightarrow {{\text{CB}}} = \left( {{\boldsymbol{b}} – {\boldsymbol{a}}} \right) \cdot \left( {{\boldsymbol{b}} + {\boldsymbol{a}}} \right)\) M1
\( = {\left| {\mathbf{b}} \right|^2} – {\left| {\mathbf{a}} \right|^2}\) A1
\( = 0\) since \(\left| {\boldsymbol{b}} \right| = \left| {\boldsymbol{a}} \right|\) R1
Note: Only award the A1 and R1 if working indicates that they understand that they are working with vectors.
so \(\overrightarrow {{\text{AB}}} \) is perpendicular to \(\overrightarrow {{\text{CB}}} \) i.e. \({\text{A}}\hat {\rm{B}}{\text{C}}\) is a right angle AG
[3 marks]
Examiners report
This question was poorly done with most candidates having difficulties in using appropriate notation which made unclear the distinction between scalars and vectors. A few candidates scored at least one of the marks in (a) but most candidates had problems in setting up the proof required in (b) with many using a circular argument which resulted in a very poor performance in this part.
This question was poorly done with most candidates having difficulties in using appropriate notation which made unclear the distinction between scalars and vectors. A few candidates scored at least one of the marks in (a) but most candidates had problems in setting up the proof required in (b) with many using a circular argument which resulted in a very poor performance in this part.
