Question hl
This question will investigate power series, as an extension to the Binomial Theorem for negative and fractional indices.
A power series in $x$ is defined as a function of the form $f(x)=a_0+a_1 x+a_2 x^2+a_3 x^3+\ldots$ where the $a_i \in \mathrm{R}$.
It can be considered as an infinite polynomial.
This is an example of a power series, but is only a finite power series, since only a finite number of the $a_i$ are non-zero.
We will now attempt to generalise further.
Suppose $(1+x)^q, q \in \mathrm{Q}$ can be written as the power series $a_0+a_1 x+a_2 x^2+a_3 x^3+\ldots$
a. Expand $(1+x)^5$ using the Binomial Theorem.
b. Consider the power series $1-x+x^2-x^3+x^4-\ldots$
By considering the ratio of consecutive terms, explain why this series is equal to $(1+x)^{-1}$ and state the values of $x$ for which this equality is true.
c. Differentiate the equation obtained part (b) and hence, find the first four terms in a power series for $(1+x)^{-2}$.
d. Repeat this process to find the first four terms in a power series for $(1+x)^{-3}$.
e. Hence, by recognising the pattern, deduce the first four terms in a power series for $(1+x)^{-n}, n \in \mathrm{Z}^{+}$.
f. By substituting $x=0$, find the value of $a_0$.
g. By differentiating both sides of the expression and then substituting $x=0$, find the value of $a_1$.
h. Repeat this procedure to find $a_2$ and $a_3$.
i. Hence, write down the first four terms in what is called the Extended Binomial Theorem for $(1+x)^q, q \in \mathrm{Q}$.
j. Write down the power series for $\frac{1}{1+x^2}$.
k. Hence, using integration, find the power series for $\arctan x$, giving the first four non-zero terms.
▶️Answer/Explanation
Markscheme
a. $1+5 x+10 x^2+10 x^3+5 x^4+x^5 \quad M 1 A 1$
[2 marks]
b. It is an infinite GP with $a=1, r=-x \quad$ R1A1
$$
S_{\infty}=\frac{1}{1-(-x)}=\frac{1}{1+x}=(1+x)^{-1} \quad \text { M1A1AG }
$$
[4 marks]
$$
\begin{aligned}
& \text { c. }(1+x)^{-1}=1-x+x^2-x^3+x^4-\ldots \\
& \begin{array}{l}
-1(1+x)^{-2}=-1+2 x-3 x^2+4 x^3-\ldots \quad \text { A1 } \\
(1+x)^{-2}=1-2 x+3 x^2-4 x^3+\ldots \quad \text { A1 }
\end{array}
\end{aligned}
$$
d. $-2(1+x)^{-3}=-2+6 x-12 x^2+20 x^3 \ldots \quad$ A1
$(1+x)^{-3}=1-3 x+6 x^2-10 x^3 \ldots \quad$ A1
[2 marks]
e. $(1+x)^{-n}=1-n x+\frac{n(n+1)}{2 !} x^2-\frac{n(n+1)(n+2)}{3 !} x^3 \ldots \quad$ A1A1A1
[3 marks]
f. $1^q=a_0 \Rightarrow a_0=1 \quad \boldsymbol{A 1}$
[1 mark]
g. $q(1+x)^{q-1}=a_1+2 a_2 x+3 a_3 x^2+\ldots \quad$ A1
$a_1=q \quad \boldsymbol{A 1}$
[2 marks]
h. $q(q-1)(1+x)^{q-2}=1 \times 2 a_2+2 \times 3 a_3 x+\ldots \quad$ A1
$$
\begin{aligned}
& a_2=\frac{q(q-1)}{2 !} \quad \text { A1 } \\
& q(q-1)(q-2)(1+x)^{q-3}=1 \times 2 \times 3 a_3+\ldots \\
& a_3=\frac{q(q-1)(q-2)}{3 !} \quad \text { A1 }
\end{aligned}
$$
A1
[4 marks]
i. $(1+x)^q=1+q x+\frac{q(q-1)}{2 !} x^2+\frac{q(q-1)(q-2)}{3 !} x^3 \ldots \quad$ A1
[1 mark]
j. $\frac{1}{1+x^2}=1-x^2+x^4-x^6+\ldots \quad$ M1A1
[2 marks]
k. $\arctan x+c=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\ldots \quad$ M1A1
Putting $x=0 \Rightarrow c=0 \quad R 1$
So $\arctan x=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\ldots \quad$ A1
[4 marks]
Question hl1.1
A polygonal number is an integer which can be represented as a series of dots arranged in the shape of a regular polygon. Triangular numbers, square numbers and pentagonal numbers are examples of polygonal numbers.
For example, a triangular number is a number that can be arranged in the shape of an equilateral triangle. The first five triangular numbers are $1,3,6,10$ and 15 .
The following table illustrates the first five triangular, square and pentagonal numbers respectively. In each case the first polygonal number is one represented by a single dot.
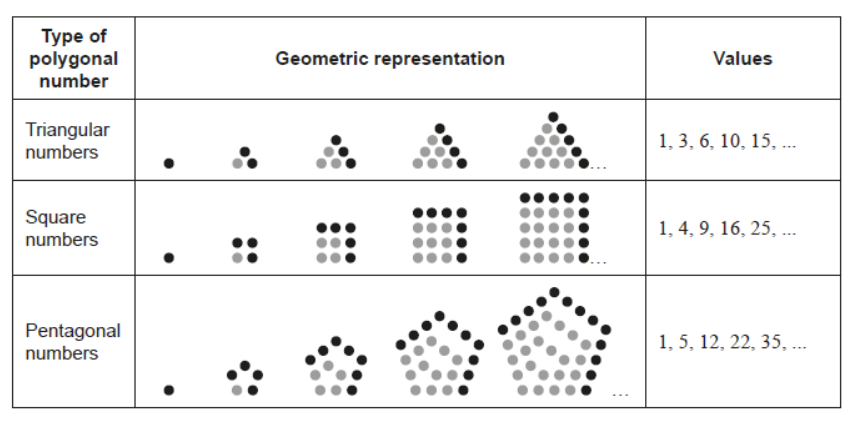
For an $r$-sided regular polygon, where $r \in \mathrm{Z}^{+}, r \geq 3$, the $n$th polygonal number $P_r(n)$ is given by
$$
P_r(n)=\frac{(r-2) n^2-(r-4) n}{2}, \text { where } n \in Z^{+} .
$$
Hence, for square numbers, $P_4(n)=\frac{(4-2) n^2-(4-4) n}{2}=n^2$.
The $n$th pentagonal number can be represented by the arithmetic series
$$
P_5(n)=1+4+7+\ldots+(3 n-2) .
$$
a.i. For triangular numbers, verify that $P_3(n)=\frac{n(n+1)}{2}$.
a.ii.The number 351 is a triangular number. Determine which one it is.
b.i. Show that $P_3(n)+P_3(n+1) \equiv(n+1)^2$.
b.ii.State, in words, what the identity given in part (b)(i) shows for two consecutive triangular numbers.
b.iiiFor $n=4$, sketch a diagram clearly showing your answer to part (b)(ii).
c. Show that $8 P_3(n)+1$ is the square of an odd number for all $n \in Z^{+}$.
d. Hence show that $P_5(n)=\frac{n(3 n-1)}{2}$ for $n \in \mathrm{Z}^{+}$.
e. By using a suitable table of values or otherwise, determine the smallest positive integer, greater than 1 , that is both a triangular number and a pentagonal number.
f. A polygonal number, $P_r(n)$, can be represented by the series
$$
\sum_{m=1}^n(1+(m-1)(r-2)) \text { where } r \in \mathbb{Z}^{+}, r \geq 3 \text {. }
$$
Use mathematical induction to prove that $P_r(n)=\frac{(r-2) n^2-(r-4) n}{2}$ where $n \in \mathbb{Z}^{+}$.
▶️Answer/Explanation
Markscheme
a.i. $P_3(n)=\frac{(3-2) n^2-(3-4) n}{2}$ OR $P_3(n)=\frac{n^2-(-n)}{2} \quad$ A1
$$
P_3(n)=\frac{n^2+n}{2} \quad \boldsymbol{A 1}
$$
Note: Award $\boldsymbol{A O A 1}$ if $P_3(n)=\frac{n^2+n}{2}$ only is seen.
Do not award any marks for numerical verification.
so for triangular numbers, $P_3(n)=\frac{n(n+1)}{2} \quad \boldsymbol{A G}$
[2 marks]
a.iiMETHOD 1
uses a table of values to find a positive integer that satisfies $P_3(n)=351$
(M1)
for example, a list showing at least 3 consecutive terms $(\ldots 325,351,378 \ldots)$
Note: Award (M1) for use of a GDC’s numerical solve or graph feature.
$n=26$ (26th triangular number)
A1
Note: Award $\boldsymbol{A O}$ for $n=-27,26$. Award $\boldsymbol{A O}$ if additional solutions besides $n=26$ are given.
METHOD 2
attempts to solve $\frac{n(n+1)}{2}=351\left(n^2+n-702=0\right)$ for $n$
(M1)
$n=\frac{-1 \pm \sqrt{1^2-4(1)(-702)}}{2}$ OR $(n-26)(n+27)=0$
$n=26$ (26th triangular number) $\quad \boldsymbol{A 1}$
Note: Award $\boldsymbol{A O}$ for $n=-27,26$. Award $\boldsymbol{A O}$ if additional solutions besides $n=26$ are given.
[2 marks]
b.i. attempts to form an expression for $P_3(n)+P_3(n+1)$ in terms of $n$
M1
d.EITHER
$$
\begin{aligned}
& P_3(n)+P_3(n+1) \equiv \frac{n(n+1)}{2}+\frac{(n+1)(n+2)}{2} \\
& \equiv \frac{(n+1)(2 n+2)}{2}\left(\equiv \frac{2(n+1)(n+1)}{2}\right) \quad \boldsymbol{A 1}
\end{aligned}
$$
OR
$$
\begin{aligned}
& P_3(n)+P_3(n+1) \equiv\left(\frac{n^2}{2}+\frac{n}{2}\right)+\left(\frac{(n+1)^2}{2}+\frac{n+1}{2}\right) \\
& \equiv\left(\frac{n^2+n}{2}\right)+\left(\frac{n^2+2 n+1+n+1}{2}\right)\left(\equiv n^2+2 n+1\right) \quad \boldsymbol{A 1}
\end{aligned}
$$
THEN
$$
\equiv(n+1)^2 \quad \boldsymbol{A G}
$$
[2 marks]
b.ii.the sum of the $n$th and $(n+1)$ th triangular numbers
is the $(n+1)$ th square number
A1
[1 mark]
b.iii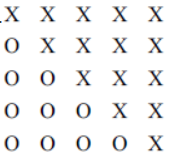
Note: Accept equivalent single diagrams, such as the one above, where the 4 th and 5 th triangular numbers and the 5 th square number are clearly shown.
Award $\boldsymbol{A} 1$ for a diagram that show $P_3(4)$ (a triangle with 10 dots) and $P_3(5)$ (a triangle with 15 dots) and $P_4(5)$ (a square with 25 dots).
[1 mark]
c. METHOD 1
$$
8 P_3(n)+1=8\left(\frac{n(n+1)}{2}\right)+1(=4 n(n+1)+1) \quad \text { A1 }
$$
attempts to expand their expression for $8 P_3(n)+1$
(M1)
$$
\begin{aligned}
& =4 n^2+4 n+1 \\
& =(2 n+1)^2 \quad \text { A1 }
\end{aligned}
$$
and $2 n+1$ is odd $\quad A G$
METHOD 2
$$
8 P_3(n)+1=8\left((n+1)^2-P_3(n+1)\right)+1\left(=8\left((n+1)^2-\frac{(n+1)(n+2)}{2}\right)+1\right) \boldsymbol{A 1}
$$
attempts to expand their expression for $8 P_3(n)+1 \quad$ (M1)
$$
\begin{aligned}
& 8\left(n^2+2 n+1\right)-4\left(n^2+3 n+2\right)+1\left(=4 n^2+4 n+1\right) \\
& =(2 n+1)^2
\end{aligned}
$$
and $2 n+1$ is odd
$\boldsymbol{A G}$
Method 3
$$
8 P_3(n)+1=8\left(\frac{n(n+1)}{2}\right)+1\left(=(A n+B)^2\right)\left(\text { where } A, B \in \mathbb{Z}^{+}\right) \quad \boldsymbol{A 1}
$$
attempts to expand their expression for $8 P_3(n)+1 \quad$ (M1)
$$
4 n^2+4 n+1\left(=A^2 n^2+2 A B n+B^2\right)
$$
now equates coefficients and obtains $B=1$ and $A=2$
$$
=(2 n+1)^2 \quad \boldsymbol{A 1}
$$
and $2 n+1$ is odd
AG
[3 marks]
$u_1=1$ and $d=3$
(A1)
substitutes their $u_1$ and their $d$ into $P_5(n)=\frac{n}{2}\left(2 u_1+(n-1) d\right) \quad$ M1
$P_5(n)=\frac{n}{2}(2+3(n-1))\left(=\frac{n}{2}(2+3 n-3)\right)$
A1
OR
$u_1=1$ and $u_n=3 n-2$
(A1)
substitutes their $u_1$ and their $u_n$ into $P_5(n)=\frac{n}{2}\left(u_1+u_n\right) \quad$ M1
$P_5(n)=\frac{n}{2}(1+3 n-2) \quad$ A1
OR
$$
\begin{aligned}
& P_5(n)=(3(1)-2)+(3(2)-2)+(3(3)-2)+\ldots 3 n-2 \\
& P_5(n)=(3(1)+3(2)+3(3)+\ldots+3 n)-2 n(=3(1+2+3+\ldots+n)-2 n)
\end{aligned}
$$
(A1)
substitutes $\frac{n(n+1)}{2}$ into their expression for $P_5(n) \quad \boldsymbol{M 1}$
$$
\begin{aligned}
& P_5(n)=3\left(\frac{n(n+1)}{2}\right)-2 n \\
& P_5(n)=\frac{n}{2}(3(n+1)-4)
\end{aligned}
$$
A1
OR
attempts to find the arithmetic mean of $n$ terms
(M1)
$$
=\frac{1+(3 n-2)}{2}
$$
A1
multiplies the above expression by the number of terms $n$
$$
P_5(n)=\frac{n}{2}(1+3 n-2) \quad \text { A1 }
$$
THEN
$$
\text { so } P_5(n)=\frac{n(3 n-1)}{2} \quad \text { AG }
$$
[3 marks]
e. METHOD 1
forms a table of $P_3(n)$ values that includes some values for $n>5$
forms a table of $P_5(m)$ values that includes some values for $m>5$
(M1)
(M1)
Note: Award $(\boldsymbol{M} 1)$ if at least one $P_3(n)$ value is correct. Award $(\boldsymbol{M} 1)$ if at least one $P_5(m)$ value is correct. Accept as above for $\left(n^2+n\right)$ values and $\left(3 m^2-m\right)$ values.
$n=20$ for triangular numbers
(A1)
$m=12$ for pentagonal numbers
(A1)
Note: Award (A1) if $n=20$ is seen in or out of a table. Award (A1) if $m=12$ is seen in or out of a table. Condone the use of the same parameter for triangular numbers and pentagonal numbers, for example, $n=20$ for triangular numbers and $n=12$ for pentagonal numbers.
210 (is a triangular number and a pentagonal number)
A1
Note: Award all five marks for 210 seen anywhere with or without working shown.
METHOD 2
EITHER
attempts to express $P_3(n)=P_5(m)$ as a quadratic in $n$
(M1)
$n^2+n+\left(m-3 m^2\right)(=0)$ (or equivalent)
attempts to solve their quadratic in $n$
(M1)
$$
n=\frac{-1 \pm \sqrt{12 m^2-4 m+1}}{2}\left(=\frac{-1 \pm \sqrt{1^2-4\left(m-3 m^2\right)}}{2}\right)
$$
OR
attempts to express $P_3(n)=P_5(m)$ as a quadratic in $m$
(M1)
$3 m^2-m-\left(n^2+n\right)(=0)$ (or equivalent)
attempts to solve their quadratic in $m$
(M1)
$$
m=\frac{1 \pm \sqrt{12 n^2-12 n+1}}{6}\left(=\frac{1 \pm \sqrt{(-1)^2+12\left(n^2+n\right)}}{6}\right)
$$
THEN
$n=20$ for triangular numbers
$m=12$ for pentagonal numbers
A1
METHOD 3
$\frac{n(n+1)}{2}=\frac{m(3 m-1)}{2}$
let $n=m+k(n>m)$ and so $3 m^2-m=(m+k)(m+k+1) \quad$ M1
$2 m^2-2(k+1) m-\left(k^2+k\right)=0$
A1
attempts to find the discriminant of their quadratic
and recognises that this must be a perfect square
M1
$\Delta=4(k+1)^2+8\left(k^2+k\right)$
$N^2=4(k+1)^2+8\left(k^2+k\right)(=4(k+1)(3 k+1))$
determines that $k=8$ leading to $2 m^2-18 m-72=0 \Rightarrow m=-3,12$ and so $m=12$
A1
210 (is a triangular number and a pentagonal number)
A1
METHOD 4
$$
\frac{n(n+1)}{2}=\frac{m(3 m-1)}{2}
$$
let $m=n-k(m<n)$ and so $n^2+n=(n-k)(3(n-k)-1) \quad$ M1
$$
2 n^2-2(3 k+1) n+\left(3 k^2+k\right)=0
$$
A1
attempts to find the discriminant of their quadratic and recognises that this must be a perfect square $\boldsymbol{M}$
$$
\begin{aligned}
& \Delta=4(3 k+1)^2-8\left(3 k^2+k\right) \\
& N^2=4(3 k+1)^2-8\left(3 k^2+k\right)(=4(k+1)(3 k+1))
\end{aligned}
$$
determines that $k=8$ leading to $2 n^2-50 n+200=0 \Rightarrow n=5,20$ and so $n=20$
A1
210 (is a triangular number and a pentagonal number)
A1
[5 marks]
f. Note: Award a maximum of R1MOMOA1M1A1A1R0 for a ‘correct’ proof using $n$ and $n+1$.
consider $n=1: P_r(1)=1+(1-1)(r-2)=1$ and $P_r(1)=\frac{(r-2)\left(1^2\right)-(r-4)(1)}{2}=1$
so true for $n=1$
R1
Note: Accept $P_r(1)=1$ and $P_r(1)=\frac{(r-2)\left(1^2\right)-(r-4)(1)}{2}=1$.
Do not accept one-sided considerations such as ‘ $P_r(1)=1$ and so true for $n=1^{\prime}$.
Subsequent marks after this $R 1$ are independent of this mark can be awarded.
Assume true for $n=k$, ie. $P_r(k)=\frac{(r-2) k^2-(r-4) k}{2} \quad \mathbf{M 1}$
Note: Award $\boldsymbol{M O}$ for statements such as “let $n=k$ “. The assumption of truth must be clear.
Subsequent marks after this $\boldsymbol{M} \boldsymbol{1}$ are independent of this mark and can be awarded.
Consider $n=k+1$ :
$\left(P_r(k+1)\right.$ can be represented by the sum
$$
\begin{aligned}
& \sum_{m=1}^{k+1}(1+(m-1)(r-2))=\sum_{m=1}^k(1+(m-1)(r-2))+(1+k(r-2)) \text { and so } \\
& P_r(k+1)=\frac{(r-2) k^2-(r-4) k}{2}+(1+k(r-2))\left(P_r(k+1)=P_r(k)+(1+k(r-2))\right) \quad \text { M1 } \\
& =\frac{(r-2) k^2-(r-4) k+2+2 k(r-2)}{2} \quad \boldsymbol{A} 1 \\
& =\frac{(r-2)\left(k^2+2 k\right)-(r-4) k+2}{2} \\
& =\frac{(r-2)\left(k^2+2 k+1\right)-(r-2)-(r-4) k+2}{2} \quad \boldsymbol{M 1} \\
& =\frac{(r-2)(k+1)^2-(r-4) k-(r-4)}{2} \\
& =\frac{(r-2)(k+1)^2-(r-4)(k+1)}{2} \\
& \text { A1 } \\
&
\end{aligned}
$$
hence true for $n=1$ and $n=k$ true $\Rightarrow n=k+1$ true $\quad R 1$ therefore true for all $n \in Z^{+}$
Note: Only award the final $\boldsymbol{R} 1$ if the first five marks have been awarded. Award marks as appropriate for solutions that expand both the LHS and (given) RHS of the equation.
[8 marks]