Question may 2022
This question asks you to explore cubic polynomials of the form $(x-r)\left(x^2-2 a x+a^2+b^2\right)$ for $x \in \mathbb{R}$ and corresponding cubic equations with one real root and two complex roots of the form $(z-r)\left(z^2-2 a z+a^2+b^2\right)=0$ for $z \in \mathrm{C}$.
In parts (a), (b) and (c), let $r=1, a=4$ and $b=1$.
Consider the equation $(z-1)\left(z^2-8 z+17\right)=0$ for $z \in \mathbb{C}$.
Consider the function $f(x)=(x-1)\left(x^2-8 x+17\right)$ for $x \in \mathbb{R}$.
Consider the function $g(x)=(x-r)\left(x^2-2 a x+a^2+b^2\right)$ for $x \in \mathbb{R}$ where $r, a \in \mathbb{R}$ and $b \in \mathbb{R}, b>0$.
The equation $(z-r)\left(z^2-2 a z+a^2+b^2\right)=0$ for $z \in \mathbb{C}$ has roots $r$ and $a \pm b$ i where $r, a \in \mathbb{R}$ and $b \in \mathbb{R}, b>0$.
On the Cartesian plane, the points $\mathrm{C}_1\left(a, \sqrt{g^{\prime}(a)}\right)$ and $\mathrm{C}_2\left(a,-\sqrt{g^{\prime}(a)}\right)$ represent the real and imaginary parts of the complex roots of the equation $(z-r)\left(z^2-2 a z+a^2+b^2\right)=0$
The following diagram shows a particular curve of the form $y=(x-r)\left(x^2-2 a x+a^2+16\right)$ and the tangent to the curve at the point $\mathrm{A}(a, 80)$. The curve and the tangent both intersect the $x$-axis at the point $\mathrm{R}(-2,0)$. The points $\mathrm{C}_1$ and $\mathrm{C}_2$ are also shown.
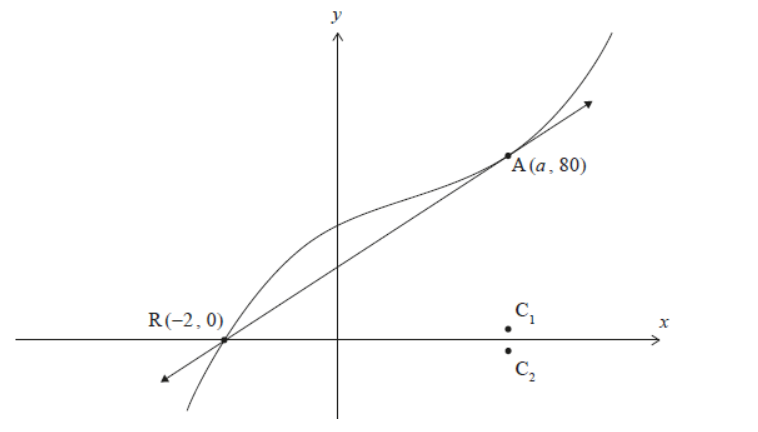
Consider the curve $y=(x-r)\left(x^2-2 a x+a^2+b^2\right)$ for $a \neq r, b>0$. The points $\mathrm{A}(a, g(a))$ and $\mathrm{R}(r, 0)$ are as defined in part (d)(ii). The curve has a point of inflexion at point $P$.
Consider the special case where $a=r$ and $b>0$.
a.i. Given that 1 and $4+\mathrm{i}$ are roots of the equation, write down the third root.
a.ii.Verify that the mean of the two complex roots is 4 .
b. Show that the line $y=x-1$ is tangent to the curve $y=f(x)$ at the point $\mathrm{A}(4,3)$.
[1]
[1]
c. Sketch the curve $y=f(x)$ and the tangent to the curve at point A, clearly showing where the tangent crosses the $x$-axis.
d.i. Show that $g^{\prime}(x)=2(x-r)(x-a)+x^2-2 a x+a^2+b^2$.
[2]
d.ii.Hence, or otherwise, prove that the tangent to the curve $y=g(x)$ at the point $\mathrm{A}(a, g(a))$ intersects the $x$-axis at the point $\mathrm{R}(r, 0)$.
e. Deduce from part (d)(i) that the complex roots of the equation $(z-r)\left(z^2-2 a z+a^2+b^2\right)=0$ can be expressed as $a \pm \mathrm{i} \sqrt{g^{\prime}(a)}$.
f.i. Use this diagram to determine the roots of the corresponding equation of the form $(z-r)\left(z^2-2 a z+a^2+16\right)=0$ for $z \in \mathbb{C}$.
f.ii. State the coordinates of $\mathrm{C}_2$.
g.i. Show that the $x$-coordinate of $\mathrm{P}$ is $\frac{1}{3}(2 a+r)$.
You are not required to demonstrate a change in concavity.
g.iiHence describe numerically the horizontal position of point $\mathrm{P}$ relative to the horizontal positions of the points $\mathrm{R}$ and $\mathrm{A}$.
[1]
h.i. Sketch the curve $y=(x-r)\left(x^2-2 a x+a^2+b^2\right)$ for $a=r=1$ and $b=2$.
h.ii.For $a=r$ and $b>0$, state in terms of $r$, the coordinates of points P and A.
[1]
▶️Answer/Explanation
Markscheme
a.i. 4 – i
A1
[1 mark]
a.iimean $=\frac{1}{2}(4+\mathrm{i}+4-\mathrm{i}) \quad \boldsymbol{A 1}$
$=4 \quad \boldsymbol{A G}$
[1 mark]
b. METHOD 1
attempts product rule differentiation
(M1)
Note: Award (M1) for attempting to express $f(x)$ as $f(x)=x^3-9 x^2+25 x-17$
$f(x)=(x-1)(2 x-8)+x^2-8 x+17\left(f(x)=3 x^2-18 x+25\right) \quad$ A1
$f(4)=1$
A1
Note: Where $f(x)$ is correct, award $\boldsymbol{A} 1$ for solving $f(x)=1$ and obtaining $x=4$.
EITHER
$$
y-3=1(x-4) \quad \text { A1 }
$$
OR
$$
\begin{aligned}
& y=x+c \\
& 3=4+c \Rightarrow c=-1
\end{aligned}
$$
A1
OR
states the gradient of $y=x-1$ is also 1 and verifies that $(4,3)$ lies on the line $y=x-1$
A1
THEN
so $y=x-1$ is the tangent to the curve at $\mathrm{A}(4,3) \quad \boldsymbol{A G}$
Note: Award a maximum of (M0)AOA1A1 to a candidate who does not attempt to find $f(x)$.
METHOD 2
sets $f(x)=x-1$ to form $x-1=(x-1)\left(x^2-8 x+17\right)$
(M1)
EITHER
$(x-1)\left(x^2-8 x+16\right)=0\left(x^3-9 x^2+24 x-16=0\right)$
attempts to solve a correct cubic equation
$$
(x-1)(x-4)^2=0 \Rightarrow x=1,4
$$
OR
recognises that $x \neq 1$ and forms $x^2-8 x+17=1\left(x^2-8 x+16=0\right)$
attempts to solve a correct quadratic equation
$$
(x-4)^2=0 \Rightarrow x=4
$$
THEN
$x=4$ is a double root
R1
A1
(M1)
(M1)
A1
so $y=x-1$ is the tangent to the curve at $\mathrm{A}(4,3) \quad \boldsymbol{A G}$
Note: Candidates using this method are not required to verify that $y=3$.
[4 marks]
c.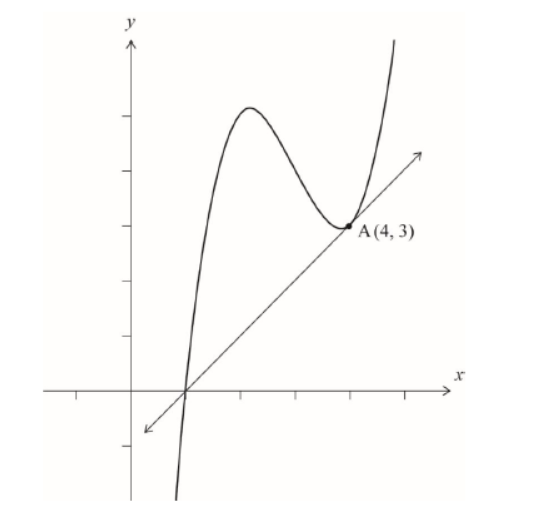
a positive cubic with an $x$-intercept $(x=1)$, and a local maximum and local minimum in the first quadrant both positioned to the left of A
$A 1$
Note: As the local minimum and point A are very close to each other, condone graphs that seem to show these points coinciding. For the point of tangency, accept labels such as A, $(4,3)$ or the point labelled from both axes. Coordinates are not required.
a correct sketch of the tangent passing through A and crossing the $x$-axis at the same point $(x=1)$ as the curve
A1
Note: Award $\boldsymbol{A 1 A O}$ if both graphs cross the $x$-axis at distinctly different points.
[2 marks]
d.i.EITHER
$$
g^{\prime}(x)=(x-r)(2 x-2 a)+x^2-2 a x+a^2+b^2
$$
(M1)A1
OR
$$
g(x)=x^3-(2 a+r) x^2+\left(a^2+b^2+2 a r\right) x-\left(a^2+b^2\right) r
$$
attempts to find $g^{\prime}(x) \quad$ M1
$$
\begin{aligned}
& g^{\prime}(x)=3 x^2-2(2 a+r) x+a^2+b^2+2 a r \\
& =2 x^2-2(a+r) x+2 a r+x^2-2 a x+a^2+b^2 \\
& \left(=2\left(x^2-a x-r x+a r\right)+x^2-2 a x+a^2+b^2\right)
\end{aligned}
$$
A1
THEN
$$
g^{\prime}(x)=2(x-r)(x-a)+x^2-2 a x+a^2+b^2 \quad \text { AG }
$$
[2 marks]
d.iiMETHOD 1
$$
\begin{aligned}
& g(a)=b^2(a-r) \\
& g^{\prime}(a)=b^2
\end{aligned}
$$
(A1)
(A1)
attempts to substitute their $g(a)$ and $g^{\prime}(a)$ into $y-g(a)=g^{\prime}(a)(x-a) \quad$ M1
$$
y-b^2(a-r)=b^2(x-a)
$$
EITHER
$$
\begin{aligned}
& y=b^2(x-r)\left(y=b^2 x-b^2 r\right) \quad \text { A1 } \\
& \text { sets } y=0 \text { so } b^2(x-r)=0 \quad \text { M1 } \\
& b>0 \Rightarrow x=r \text { OR } b \neq 0 \Rightarrow x=r \quad \text { R1 }
\end{aligned}
$$
OR
$$
\begin{array}{ll}
\text { sets } y=0 \text { so }-b^2(a-r)=b^2(x-a) & \text { M1 } \\
b>0 \text { OR } b \neq 0 \Rightarrow-(a-r)=x-a & \text { R1 } \\
x=r \quad \text { A1 } &
\end{array}
$$
THEN
so the tangent intersects the $x$-axis at the point $\mathrm{R}(r, 0) \quad \boldsymbol{A G}$
METHOD 2
$$
\begin{aligned}
& g^{\prime}(a)=b^2 \\
& g(a)=b^2(a-r)
\end{aligned}
$$
attempts to substitute their $g(a)$ and $g^{\prime}(a)$ into $y=g^{\prime}(a) x+c$ and attempts to find $c \quad \boldsymbol{M 1}$
$$
c=-b^2 r
$$
EITHER
$$
\begin{aligned}
& y=b^2(x-r)\left(y=b^2 x-b^2 r\right) \quad \text { A1 } \\
& \text { sets } y=0 \text { so } b^2(x-r)=0 \quad \text { M1 } \\
& b>0 \Rightarrow x=r \text { OR } b \neq 0 \Rightarrow x=r
\end{aligned}
$$
R1
OR
$$
\begin{aligned}
& \text { sets } y=0 \text { so } b^2(x-r)=0 \quad \text { M1 } \\
& b>0 \text { OR } b \neq 0 \Rightarrow x-r=0 \quad \text { R1 } \\
& x=r \quad \text { A1 }
\end{aligned}
$$
METHOD 3
$$
g^{\prime}(a)=b^2
$$
the line through $R(r, 0)$ parallel to the tangent at $\mathrm{A}$ has equation $y=b^2(x-r) \quad \boldsymbol{A 1}$
sets $g(x)=b^2(x-r)$ to form $b^2(x-r)=(x-r)\left(x^2-2 a x+a^2+b^2\right) \quad$ M1
$b^2=x^2-2 a x+a^2+b^2,(x \neq r) \quad \boldsymbol{A} 1$
$(x-a)^2=0$
A1
since there is a double root $(x=a)$, this parallel line through $R(r, 0)$ is the required tangent at $\mathrm{A}$
R1
[6 marks]
e. EITHER
$g^{\prime}(a)=b^2 \Rightarrow b=\sqrt{g^{\prime}(a)}($ since $b>0) \quad$ R1
Note: Accept $b= \pm \sqrt{g^{\prime}(a)}$.
OR
$(a \pm b \mathrm{i}=) a \pm \mathrm{i} \sqrt{b^2}$ and $g^{\prime}(a)=b^2 \quad$ R1
THEN
hence the complex roots can be expressed as $a \pm \mathrm{i} \sqrt{g^{\prime}(a)} \quad \quad \boldsymbol{A G}$
[1 mark]
f.i. $b=4$ (seen anywhere)
A1
EITHER
attempts to find the gradient of the tangent in terms of $a$ and equates to 16
(M1)
OR
substitutes $r=-2, x=a$ and $y=80$ to form $80=(a-(-2))\left(a^2-2 a^2+a^2+16\right)$
(M1)
OR
substitutes $r=-2, x=a$ and $y=80$ into $y=16(x-r)$
(M1)
THEN
$\frac{80}{a+2}=16 \Rightarrow a=3$
roots are -2 (seen anywhere) and $3 \pm 4 \mathrm{i}$
A1A1
Note: Award $\boldsymbol{A} \boldsymbol{1}$ for -2 and $\boldsymbol{A} \boldsymbol{1}$ for $3 \pm 4$ i. Do not accept coordinates.
[4 marks]
f.ii. $(3,-4)$
A1
Note: Accept ” $x=3$ and $y=-4$ “.
Do not award $\boldsymbol{A 1 F T}$ for $(a,-4)$.
[1 mark]
g.i. $g^{\prime}(x)=2(x-r)(x-a)+x^2-2 a x+a^2+b^2$
attempts to find $g^{\prime \prime}(x) \quad M 1$
$g^{\prime \prime}(x)=2(x-a)+2(x-r)+2 x-2 a(=6 x-2 r-4 a)$
sets $g^{\prime \prime}(x)=0$ and correctly solves for $x \quad A 1$
for example, obtaining $x-r+2(x-a)=0$ leading to $3 x=2 a+r$
So $x=\frac{1}{3}(2 a+r) \quad$ AG
Note: Do not award $\boldsymbol{A} \boldsymbol{1}$ if the answer does not lead to the $\boldsymbol{A G}$.
[2 marks]
g.iipoint $\mathrm{P}$ is $\frac{2}{3}$ of the horizontal distance (way) from point $\mathrm{R}$ to point A
A1
Note: Accept equivalent numerical statements or a clearly labelled diagram displaying the numerical relationship. Award $\mathbf{A O}$ for non-numerical statements such as ” $\mathrm{P}$ is between $\mathrm{R}$ and $\mathrm{A}$, closer to $\mathrm{A}$ “.
[1 mark]
h.i. $y=(x-1)\left(x^2-2 x+5\right)$
(A1)
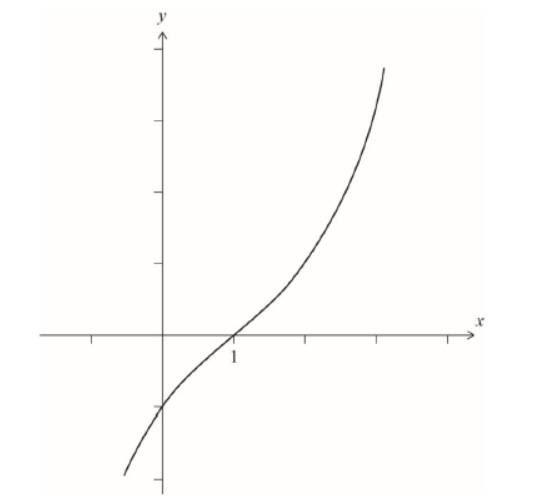
a positive cubic with no stationary points and a non-stationary point of inflexion at $x=1$
A1
Note: Graphs may appear approximately linear. Award this $\boldsymbol{A 1}$ if a change of concavity either side of $x=1$ is apparent. Coordinates are not required and the $y$-intercept need not be indicated.
[2 marks]
h.ii. $(r, 0) \quad \boldsymbol{A 1}$
[1 mark]
Question
Question
A Gaussian integer is a complex number, $z$, such that $z=a+b$ i where $a, b \in \mathrm{Z}$. In this question, you are asked to investigate certain divisibility properties of Gaussian integers.
Consider two Gaussian integers, $\alpha=3+4 \mathrm{i}$ and $\beta=1-2 \mathrm{i}$, such that $\gamma=\alpha \beta$ for some Gaussian integer $\gamma$.
Now consider two Gaussian integers, $\alpha=3+4 \mathrm{i}$ and $\gamma=11+2 \mathrm{i}$.
The norm of a complex number $z$, denoted by $N(z)$, is defined by $N(z)=|z|^2$. For example, if $z=2+3 \mathrm{i}$ then $N(2+3 \mathrm{i})=2^2+3^2=13$.
A Gaussian prime is a Gaussian integer, $z$, that cannot be expressed in the form $z=\alpha \beta$ where $\alpha, \beta$ are Gaussian integers with $N(\alpha), N(\beta)>1$.
The positive integer 2 is a prime number, however it is not a Gaussian prime.
Let $\alpha, \beta$ be Gaussian integers.
The result from part ( $\mathrm{h}$ ) provides a way of determining whether a Gaussian integer is a Gaussian prime.
a. Find $\gamma$.
b. Determine whether $\frac{\gamma}{\alpha}$ is a Gaussian integer.
c. On an Argand diagram, plot and label all Gaussian integers that have a norm less than 3 .
[2]
d. Given that $\alpha=a+b$ i where $a, b \in \mathrm{Z}$, show that $N(\alpha)=a^2+b^2$.
e. By expressing the positive integer $n=c^2+d^2$ as a product of two Gaussian integers each of norm $c^2+d^2$, show that $n$ is not a Gaussian prime.
[3]
f. Verify that 2 is not a Gaussian prime.
[2]
g. Write down another prime number of the form $c^2+d^2$ that is not a Gaussian prime and express it as a product of two Gaussian integers.
[2]
h. Show that $N(\alpha \beta)=N(\alpha) N(\beta)$.
i. Hence show that $1+4 \mathrm{i}$ is a Gaussian prime.
[3]
j. Use proof by contradiction to prove that a prime number, $p$, that is not of the form $a^2+b^2$ is a Gaussian prime.
[6]
▶️Answer/Explanation
Markscheme
a. ${ }^{\star}$ This sample question was produced by experienced DP mathematics senior examiners to aid teachers in preparing for external assessment in the new MAA course. There may be minor differences in formatting compared to formal exam papers.
$$
(3+4 i)(1-2 i)=11-2 \mathrm{i}
$$
(M1)A1
[2 marks]
b. $\frac{\gamma}{\alpha}=\frac{41}{25}-\frac{38}{25} \mathrm{i}$
(M1)A1
(Since $\operatorname{Re}_{\frac{\gamma}{\alpha}}^{\frac{\gamma}{2}}\left(=\frac{41}{25}\right)$ and/or $\operatorname{Im}_\alpha^{\frac{\gamma}{\alpha}}\left(=-\frac{38}{25}\right)$ are not integers) $\frac{\gamma}{\alpha}$ is not a Gaussian integer $\quad \boldsymbol{R 1}$
Note: Award $\boldsymbol{R} \mathbf{1}$ for correct conclusion from their answer.
[3 marks]
c. $\pm 1, \pm \mathrm{i}, 0$ plotted and labelled
$1 \pm \mathrm{i}, \quad-1 \pm \mathrm{i}$ plotted and labelled
A1
A1
Note: Award $A 1 A O$ if extra points to the above are plotted and labelled.
[2 marks]
d. $|z|=\sqrt{a^2+b^2}\left(\right.$ and as $\left.N(z)=|z|^2\right) \quad \boldsymbol{A 1}$
then $N(\alpha)=a^2+b^2 \quad \boldsymbol{A G}$
[1 mark]
e. $c^2+d^2=(c+d \mathrm{i})(c-d \mathrm{i}) \quad \boldsymbol{A 1}$
and $N(c+d \mathrm{i})=N(c-d \mathrm{i})=c^2+d^2 \quad \boldsymbol{R} \mathbf{1}$
$N(c+d \mathrm{i}), N(c-d \mathrm{i})>1$ (since $c, d$ are positive) $\boldsymbol{R} 1$
so $c^2+d^2$ is not a Gaussian prime, by definition $\boldsymbol{A G}$
[3 marks]
f. $2\left(=1^2+1^2\right)=(1+\mathrm{i})(1-\mathrm{i})$
(A1)
$N(1+\mathrm{i})=N(1-\mathrm{i})=2$
A1
so 2 is not a Gaussian prime
AG
[2 marks]
g. For example, $5\left(=1^2+2^2\right)=(1+2 \mathrm{i})(1-2 \mathrm{i}) \quad$ (M1)A1
h. METHOD 1
Let $\alpha=m+n \mathrm{i}$ and $\beta=p+q \mathrm{i}$
LHS:
$$
\begin{aligned}
& \alpha \beta=(m p-n q)+(m q+n p) \mathrm{i} \quad \text { M1 } \\
& N(\alpha \beta)=(m p-n q)^2+(m q+n p)^2 \quad \text { A1 } \\
& (m p)^2-2 m n p q+(n q)^2+(m q)^2+2 m n p q+(n p)^2 \\
& (m p)^2+(n q)^2+(m q)^2+(n p)^2 \quad \text { A1 }
\end{aligned}
$$
A1
A1
RHS:
$$
\begin{aligned}
& N(\alpha) N(\beta)=\left(m^2+n^2\right)\left(p^2+q^2\right) \quad \text { M1 } \\
& (m p)^2+(m q)^2+(n p)^2+(n q)^2 \quad \text { A1 } \\
& \text { LHS = RHS and so } N(\alpha \beta)=N(\alpha) N(\beta) \quad \text { AG }
\end{aligned}
$$
METHOD 2
Let $\alpha=m+n \mathrm{i}$ and $\beta=p+q \mathrm{i}$
LHS
$$
\begin{aligned}
& N(\alpha \beta)=\left(m^2+n^2\right)\left(p^2+q^2\right) \quad \text { M1 } \\
& =(m+n \mathrm{i})(m-n \mathrm{i})(p+q \mathrm{i})(p-q \mathrm{i}) \quad \boldsymbol{A 1} \\
& =(m+n \mathrm{i})(p+q \mathrm{i})(m-n \mathrm{i})(p-q \mathrm{i}) \\
& =((m p-n q)+(m q+n p) \mathrm{i})((m p-n q)-(m q+n p) \mathrm{i}) \quad \text { M1A1 } \\
& =(m p-n q)^2+(m q+n p)^2 \quad \boldsymbol{A 1} \\
& N=((m p-n q)+(m q+n p) \mathrm{i}) \quad \boldsymbol{A 1} \\
& =N(\alpha) N(\beta)(=\mathrm{RHS}) \quad \boldsymbol{A G}
\end{aligned}
$$
A1
A1
[6 marks]
i. $N(1+4 \mathrm{i})=17$ which is a prime (in $\mathrm{Z}$ ) $\quad \boldsymbol{R} 1$
if $1+4 \mathrm{i}=\alpha \beta$ then $17=N(\alpha \beta)=N(\alpha) N(\beta) \quad$ R1
we cannot have $N(\alpha), N(\beta)>1 \quad \boldsymbol{R 1}$
Note: Award $\boldsymbol{R} 1$ for stating that $1+4 \mathrm{i}$ is not the product of Gaussian integers of smaller norm because no such norms divide 17
so $1+4$ is a Gaussian prime
$A G$
[3 marks]
j. Assume $p$ is not a Gaussian prime
$\Rightarrow p=\alpha \beta$ where $\alpha, \beta$ are Gaussian integers and $N(\alpha), N(\beta)>1 \quad$ M1
$$
\Rightarrow N(p)=N(\alpha) N(\beta) \quad \text { M1 }
$$
$p^2=N(\alpha) N(\beta) \quad \boldsymbol{A 1}$
It cannot be $N(\alpha)=1, N(\beta)=p^2$ from definition of Gaussian prime $\quad$ R1 hence $N(\alpha)=p, N(\beta)=p \quad$ R1
If $\alpha=a+b \mathrm{i}$ then $N(\alpha)=a^2+b^2=p$ which is a contradiction $\quad \boldsymbol{R} \mathbf{1}$ hence a prime number, $p$, that is not of the form $a^2+b^2$ is a Gaussian prime $\quad \boldsymbol{A G}$
[6 marks]
Question
Question
In this question you will explore some of the properties of special functions $f$ and $g$ and their relationship with the trigonometric functions, sine and cosine.
Functions $f$ and $g$ are defined as $f(z)=\frac{\mathrm{e}^z+\mathrm{e}^{-z}}{2}$ and $g(z)=\frac{\mathrm{e}^z-\mathrm{e}^{-z}}{2}$, where $z \in \mathbb{C}$.
Consider $t$ and $u$, such that $t, u \in \mathbb{R}$.
Using $\mathrm{e}^{\mathrm{i} u}=\cos u+\mathrm{i} \sin u$, find expressions, in terms of $\sin u$ and $\cos u$, for
The functions $\cos x$ and $\sin x$ are known as circular functions as the general point $(\cos \theta, \sin \theta)$ defines points on the unit circle with equation $x^2+y^2=1$. The functions $f(x)$ and $g(x)$ are known as hyperbolic functions, as the general point $(f(\theta), g(\theta))$ defines points on a curve known as a hyperbola with equation $x^2-y^2=1$. This hyperbola has two asymptotes.
a. Verify that $u=f(t)$ satisfies the differential equation $\frac{d^2 u}{d t^2}=u$.
[5]
b. Show that $(f(t))^2+(g(t))^2=f(2 t)$.
c.i. $f(\mathrm{i} i)$.
[3]
c.ii.g(iu).
[2]
d. Hence find, and simplify, an expression for $(f(\mathrm{i} u))^2+(g(\mathrm{i} u))^2$.
[2]
e. Show that $(f(t))^2-(g(t))^2=(f(1 u))^2-(g(1 u))^2$.
f. Sketch the graph of $x^2-y^2=1$, stating the coordinates of any axis intercepts and the equation of each asymptote.
g. The hyperbola with equation $x^2-y^2=1$ can be rotated to coincide with the curve defined by $x y=k, k \in \mathbb{R}$. Find the possible values of $k$.
▶️Answer/Explanation
Markscheme
a. $f(t)=\frac{\mathrm{e}^t-\mathrm{e}^{-t}}{2}$
A1
$$
\begin{array}{ll}
f^{\prime \prime}(t)=\frac{\mathrm{e}^t+\mathrm{e}^{-t}}{2} & \\
=f(t) \quad \text { AG }
\end{array}
$$
A1
[2 marks]
b. METHOD 1
$$
(f(t))^2+(g(t))^2
$$
substituting $f$ and $g$
M1
$$
\begin{aligned}
& =\frac{\left(\mathrm{e}^t+\mathrm{e}^{-t}\right)^2+\left(\mathrm{e}^t-\mathrm{e}^{-t}\right)^2}{4} \\
& =\frac{\left(\mathrm{e}^t\right)^2+2+\left(\mathrm{e}^{-t}\right)^2+\left(\mathrm{e}^t\right)^2-2+\left(\mathrm{e}^{-t}\right)^2}{4} \\
& =\frac{\left(\mathrm{e}^t\right)^2+\left(\mathrm{e}^{-t}\right)^2}{2}\left(=\frac{\mathrm{e}^{2 t}+\mathrm{e}^{-2 t}}{2}\right) \\
& =f(2 t) \quad \boldsymbol{A G}
\end{aligned}
$$
(M1)
A1
METHOD 2
$$
\begin{aligned}
& f(2 t)=\frac{\mathrm{e}^{2 t}+\mathrm{e}^{-2 t}}{2} \\
& =\frac{\left(\mathrm{e}^t\right)^2+\left(\mathrm{e}^{-t}\right)^2}{2} \quad \text { M1 } \\
& =\frac{\left(\mathrm{e}^t+\mathrm{e}^{-t}\right)^2+\left(\mathrm{e}^t-\mathrm{e}^{-t}\right)^2}{4} \quad \text { M1A1 } \\
& =(f(t))^2+(g(t))^2
\end{aligned}
$$
Note: Accept combinations of METHODS 1 \& 2 that meet at equivalent expressions.
[3 marks]
c.i. substituting $\mathrm{e}^{\mathrm{i} u}=\cos u+\mathrm{i} \sin u$ into the expression for $f$
(M1)
obtaining $\mathrm{e}^{-\mathrm{i} u}=\cos u-\mathrm{i} \sin u$
(A1)
$$
f(\mathrm{i} u)=\frac{\cos u+\mathrm{i} \sin u+\cos u-\mathrm{i} \sin u}{2}
$$
Note: The $\boldsymbol{M} 1$ can be awarded for the use of sine and cosine being odd and even respectively.
$$
\begin{aligned}
& =\frac{2 \cos u}{2} \\
& =\cos u
\end{aligned}
$$
A1
[3 marks]
$$
\text { c.iig } g(i u)=\frac{\cos u+i \sin u-\cos u+i \sin u}{2}
$$
substituting and attempt to simplify
(M1)
$$
\begin{aligned}
& =\frac{2 \mathrm{i} \sin u}{2} \\
& =\mathrm{i} \sin u
\end{aligned}
$$
A1
[2 marks]
d. METHOD 1
$\left(f(\mathrm{i} u)^2+\left(g(\mathrm{i} u)^2\right.\right.$
substituting expressions found in part (c)
(M1)
$=\cos ^2 u-\sin ^2 u(=\cos 2 u)$
A1
METHOD 2
$$
\begin{aligned}
& f(2 \mathrm{i} u)=\frac{\mathrm{e}^{2 \mathrm{iu}}+\mathrm{e}^{-2 \mathrm{i} u}}{2} \\
& =\frac{\cos 2 u+\mathrm{i} \sin 2 u+\cos 2 u-\mathrm{i} \sin 2 u}{2} \\
& =\cos 2 u \quad \boldsymbol{A 1}
\end{aligned}
$$
A1
M1
Note: Accept equivalent final answers that have been simplified removing all imaginary parts eg $2 \cos ^2 u-1$ etc
[2 marks]
e.
$$
\begin{aligned}
& (f(t))^2-(g(t))^2=\frac{\left(\mathrm{e}^t+\mathrm{e}^{-t}\right)^2-\left(\mathrm{e}^t-\mathrm{e}^{-t}\right)^2}{4} \\
& =\frac{\left(\mathrm{e}^{2 t}+\mathrm{e}^{-2 t}+2\right)-\left(\mathrm{e}^{2 t}+\mathrm{e}^{-2 t}-2\right)}{4} \quad \text { M1 } \\
& =\frac{4}{4}=1 \quad \text { A1 }
\end{aligned}
$$
A1
A1
Note: Award $\boldsymbol{A} 1$ for a value of 1 obtained from either LHS or RHS of given expression.
$$
\begin{aligned}
& (f(\mathrm{i} u))^2-(g(\mathrm{i} u))^2=\cos ^2 u+\sin ^2 u \quad \text { M1 } \\
& =1\left(\text { hence }(f(t))^2-(g(t))^2=(f(\mathrm{i} u))^2-(g(\mathrm{i} u))^2\right) \quad \boldsymbol{A G} \\
&
\end{aligned}
$$
Note: Award full marks for showing that $(f(z))^2-(g(z))^2=1, \forall z \in \mathbb{C}$.
[4 marks]
f.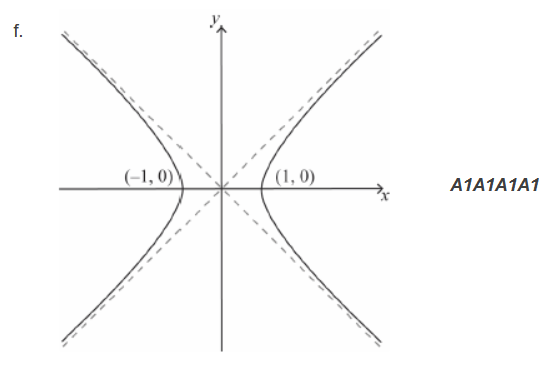
Note: Award $\boldsymbol{A} \mathbf{1}$ for correct curves in the upper quadrants, $\boldsymbol{A} \boldsymbol{1}$ for correct curves in the lower quadrants, $\boldsymbol{A} \boldsymbol{1}$ for correct $x$-intercepts of ( $-1,0$ ) and $(1,0)$ (condone $x=-1$ and 1), $\boldsymbol{A 1}$ for $y=x$ and $y=-x$.
[4 marks]
g. attempt to rotate by $45^{\circ}$ in either direction
(M1)
Note: Evidence of an attempt to relate to a sketch of $x y=k$ would be sufficient for this (M1).
attempting to rotate a particular point, eg $(1,0)$
(M1)
$(1,0)$ rotates to $\left(\frac{1}{\sqrt{2}}, \pm \frac{1}{\sqrt{2}}\right)$ (or similar)
(A1)
hence $k= \pm \frac{1}{2}$
A1A1
[5 marks]
Question
This question asks you to investigate and prove a geometric property involving the roots of the equation $z^n=1$ where $z \in \mathbb{C}$ for integers $n$, where $n \geq 2$.
The roots of the equation $z^n=1$ where $z \in \mathbb{C}$ are $1, \omega, \omega^2, \ldots, \omega^{n-1}$, where $\omega=\mathrm{e}^{\frac{2 \pi i}{n}}$. Each root can be represented by a point $\mathrm{P}_0, \mathrm{P}_1, \mathrm{P}_2, \ldots, \mathrm{P}_{n-1}$, respectively, on an Argand diagram.
For example, the roots of the equation $z^2=1$ where $z \in \mathbb{C}$ are 1 and $\omega$. On an Argand diagram, the root 1 can be represented by a point $\mathrm{P}_0$ and the root $\omega$ can be represented by a point $\mathrm{P}_1$.
Consider the case where $n=3$.
The roots of the equation $z^3=1$ where $z \in \mathbb{C}$ are $1, \omega$ and $\omega^2$. On the following Argand diagram, the points $\mathrm{P}_0, \mathrm{P}_1$ and $\mathrm{P}_2$ lie on a circle of radius 1 unit with centre $\mathrm{O}(0,0)$.

Line segments $\left[\mathrm{P}_0 \mathrm{P}_1\right]$ and $\left[\mathrm{P}_0 \mathrm{P}_2\right]$ are added to the Argand diagram in part (a) and are shown on the following Argand diagram.

$\mathrm{P}_0 \mathrm{P}_1$ is the length of $\left[\mathrm{P}_0 \mathrm{P}_1\right]$ and $\mathrm{P}_0 \mathrm{P}_2$ is the length of $\left[\mathrm{P}_0 \mathrm{P}_2\right]$.
Consider the case where $n=4$.
The roots of the equation $z^4=1$ where $z \in \mathbb{C}$ are $1, \omega, \omega^2$ and $\omega^3$.
On the following Argand diagram, the points $\mathrm{P}_0, \mathrm{P}_1, \mathrm{P}_2$ and $\mathrm{P}_3$ lie on a circle of radius 1 unit with centre $\mathrm{O}(0,0)$. $\left[\mathrm{P}_0 \mathrm{P}_1\right],\left[\mathrm{P}_0 \mathrm{P}_2\right]$ and $\left[\mathrm{P}_0 \mathrm{P}_3\right]$ are line segments.

For the case where $n=5$, the equation $z^5=1$ where $z \in \mathbb{C}$ has roots $1, \omega, \omega^2, \omega^3$ and $\omega^4$.
It can be shown that $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2 \times \mathrm{P}_0 \mathrm{P}_3 \times \mathrm{P}_0 \mathrm{P}_4=5$.
Now consider the general case for integer values of $n$, where $n \geq 2$.
The roots of the equation $z^n=1$ where $z \in \mathbb{C}$ are $1, \omega, \omega^2, \ldots, \omega^{n-1}$. On an Argand diagram, these roots can be represented by the points $\mathrm{P}_0, \mathrm{P}_1, \mathrm{P}_2, \ldots, \mathrm{P}_{n-1}$ respectively where $\left[\mathrm{P}_0 \mathrm{P}_1\right],\left[\mathrm{P}_0 \mathrm{P}_2\right], \ldots,\left[\mathrm{P}_0 \mathrm{P}_{n-1}\right]$ are line segments. The roots lie on a circle of radius 1 unit with centre $\mathrm{O}(0,0)$.
$\mathrm{P}_0 \mathrm{P}_1$ can be expressed as $|1-\omega|$.
Consider $z^n-1=(z-1)\left(z^{n-1}+z^{n-2}+\ldots+z+1\right)$ where $z \in \mathbb{C}$.
a.i. Show that $(\omega-1)\left(\omega^2+\omega+1\right)=\omega^3-1$.
a.ii.Hence, deduce that $\omega^2+\omega+1=0$.
b. Show that $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2=3$.
c. By factorizing $z^4-1$, or otherwise, deduce that $\omega^3+\omega^2+\omega+1=0$.
d. Show that $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2 \times \mathrm{P}_0 \mathrm{P}_3=4$.
e. Suggest a value for $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2 \times \ldots \times \mathrm{P}_0 \mathrm{P}_{n-1}$.
f.i. Write down expressions for $\mathrm{P}_0 \mathrm{P}_2$ and $\mathrm{P}_0 \mathrm{P}_3$ in terms of $\omega$.
f.ii. Hence, write down an expression for $\mathrm{P}_0 \mathrm{P}_{n-1}$ in terms of $n$ and $\omega$.
g.i.Express $z^{n-1}+z^{n-2}+\ldots+z+1$ as a product of linear factors over the set $\mathbb{C}$.
g.ii.Hence, using the part (g)(i) and part (f) results, or otherwise, prove your suggested result to part (e).
▶️Answer/Explanation
a.i. METHOD 1
attempts to expand $(\omega-1)\left(\omega^2+\omega+1\right)$
(M1)
$=\omega^3+\omega^2+\omega-\omega^2-\omega-1$
A1
$=\omega^3-1 \quad$ AG
METHOD 2
attempts polynomial division on $\frac{\omega^3-1}{\omega-1} \quad$ M1
$$
\begin{aligned}
& =\omega^2+\omega+1 \\
& \text { so }(\omega-1)\left(\omega^2+\omega+1\right)=\omega^3-1
\end{aligned}
$$
AG
Note: In part (a), award marks as appropriate where $\omega$ has been converted into Cartesian, modulus-argument (polar) or Euler form.
[2 marks]
a.ii.(since $\omega$ is a root of $\left.z^3=1\right) \Rightarrow \omega^3-1=0 \quad \boldsymbol{R 1}$
and $\omega \neq 1 \quad \boldsymbol{R 1}$
$\Rightarrow \omega^2+\omega+1=0 \quad A G$
Note: In part (a), award marks as appropriate where $\omega$ has been converted into Cartesian, modulus-argument (polar) or Euler form.
[2 marks]
b. METHOD 1
attempts to find either $\mathrm{P}_0 \mathrm{P}_1$ or $\mathrm{P}_0 \mathrm{P}_2$
(M1)
accept any valid method
e.g. $2 \sin \frac{\pi}{3}, 1^2+1^2-2 \cos \frac{2 \pi}{3}, \frac{1}{\sin \frac{\pi}{6}}=\frac{\mathrm{P}_0 \mathrm{P}_1}{\sin \frac{2 \pi}{3}}$ from either $\Delta \mathrm{OP}_0 \mathrm{P}_1$ or $\Delta \mathrm{OP}_0 \mathrm{P}_2$
e.g. use of Pythagoras’ theorem
e.g. $\left|1-\mathrm{e}^{\mathrm{i} \frac{2 \pi}{3}}\right|,\left|1-\left(-\frac{1}{2}+\frac{\sqrt{3}}{2} \mathrm{i}\right)\right|$ by calculating the distance between 2 points
$\mathrm{P}_0 \mathrm{P}_1=\sqrt{3} \quad \boldsymbol{A 1}$
$\mathrm{P}_0 \mathrm{P}_2=\sqrt{3} \quad \boldsymbol{A 1}$
Note: Award a maximum of M1A1AO for any decimal approximation seen in the calculation of either $\mathrm{P}_0 \mathrm{P}_1$ or $\mathrm{P}_0 \mathrm{P}_2$ or both.
so $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2=3 \quad$ AG
METHOD 2
attempts to find $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2=|1-\omega|\left|1-\omega^2\right| \quad$ (M1)
$\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2=\left|\omega^3-\omega^2-\omega+1\right| \quad$ A1
$=\left|1-\left(\omega^2+\omega+1\right)+2\right|$ and since $\omega^2+\omega+1=0 \quad \boldsymbol{R 1}$
so $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2=3 \quad$ AG
[3 marks]
C. METHOD 1
$$
z^4-1=(z-1)\left(z^3+z^2+z+1\right)
$$
A1
( $\omega$ is a root hence) $\omega^4-1=0$ and $\omega \neq 1$
R1
$$
\Rightarrow \omega^3+\omega^2+\omega+1=0
$$
AG
Note: Condone the use of $\omega$ throughout.
METHOD 2
considers the sum of roots of $z^4-1=0$
(M1)
the sum of roots is zero (there is no $z^3$ term)
A1
$$
\Rightarrow \omega^3+\omega^2+\omega+1=0
$$
AG
METHOD 3
substitutes for $\omega$
(M1)
e.g. $\mathrm{LHS}=\mathrm{e}^{\mathrm{i} \frac{3 \pi}{2}}+\mathrm{e}^{\pi \mathrm{i}}+\mathrm{e}^{\mathrm{i} \frac{\pi}{2}}+1$
$$
=-\mathrm{i}-1+\mathrm{i}+1
$$
A1
Note: This can be demonstrated geometrically or by using vectors. Accept Cartesian or modulus-argument (polar) form.
$\Rightarrow \omega^3+\omega^2+\omega+1=0$
$A G$
METHOD 4
$$
\begin{aligned}
& \omega^3+\omega^2+\omega+1=\frac{\omega^4-1}{\omega-1} \quad \text { A1 } \\
& =\frac{0}{\omega-1}=0 \text { as } \omega \neq 1 \quad \text { R1 } \\
& \Rightarrow \omega^3+\omega^2+\omega+1=0 \quad \text { AG }
\end{aligned}
$$
A1
$A G$
[2 marks]
f.ii. $\mathrm{P}_0 \mathrm{P}_{n-1}=\left|1-\omega^{n-1}\right|$
A1A1
Note: Accept $|1-\omega|$ from symmetry.
[1 mark]
g.i. $z^n-1=(z-1)\left(z^{n-1}+z^{n-2}+\ldots+z+1\right)$
considers the equation $z^{n-1}+z^{n-2}+\ldots+z+1=0 \quad$ (M1)
the roots are $\omega, \omega^2, \ldots, \omega^{n-1}$
(A1)
so $(z-\omega)\left(z-\omega^2\right) \ldots\left(z-\omega^{n-1}\right)$
A1
[3 marks]
g.ii.METHOD 1
substitutes $z=1$ into $(z-\omega)\left(z-\omega^2\right) \ldots\left(z-\omega^{n-1}\right) \equiv z^{n-1}+z^{n-2}+\ldots+z+1 \quad$ M1
$(1-\omega)\left(1-\omega^2\right) \ldots\left(1-\omega^{n-1}\right)=n$
(A1)
takes modulus of both sides M1
$$
\begin{aligned}
& \left|(1-\omega)\left(1-\omega^2\right) \ldots\left(1-\omega^{n-1}\right)\right|=|n| \\
& |1-\omega|\left|1-\omega^2\right| \ldots\left|1-\omega^{n-1}\right|=n
\end{aligned}
$$
so $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2 \times \ldots \times \mathrm{P}_0 \mathrm{P}_{n-1}=n$
AG
Note: Award a maximum of M1A1FTM1AO from part (e).
METHOD 2
$(1-\omega),\left(1-\omega^2\right), \ldots,\left(1-\omega^{n-1}\right)$ are the roots of $(1-v)^{n-1}+(1-v)^{n-2}+\ldots+(1-v)+1=0 \quad$ M1 coefficient of $v^{n-1}$ is $(-1)^{n-1}$ and the coefficient of 1 is $n$
A1
product of the roots is $\frac{(-1)^{n-1} n}{(-1)^{n-1}}=n$
A1
$$
|1-\omega|\left|1-\omega^2\right| \ldots\left|1-\omega^{n-1}\right|=n
$$
A1
so $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2 \times \ldots \times \mathrm{P}_0 \mathrm{P}_{n-1}=n$
$A G$
[4 marks]