Question nov 2021
In this question you will explore some of the properties of special functions $f$ and $g$ and their relationship with the trigonometric functions, sine and cosine.
Functions $f$ and $g$ are defined as $f(z)=\frac{\mathrm{e}^z+\mathrm{e}^{-z}}{2}$ and $g(z)=\frac{\mathrm{e}^z-\mathrm{e}^{-z}}{2}$, where $z \in \mathbb{C}$.
Consider $t$ and $u$, such that $t, u \in \mathbb{R}$.
Using $\mathrm{e}^{\mathrm{i} u}=\cos u+\mathrm{i} \sin u$, find expressions, in terms of $\sin u$ and $\cos u$, for
The functions $\cos x$ and $\sin x$ are known as circular functions as the general point $(\cos \theta, \sin \theta)$ defines points on the unit circle with equation $x^2+y^2=1$.
The functions $f(x)$ and $g(x)$ are known as hyperbolic functions, as the general point $(f(\theta), g(\theta))$ defines points on a curve known as a hyperbola with equation $x^2-y^2=1$. This hyperbola has two asymptotes.
a. Verify that $u=f(t)$ satisfies the differential equation $\frac{\mathrm{d}^2 u}{\mathrm{~d} t^2}=u$.
b. Show that $(f(t))^2+(g(t))^2=f(2 t)$.
c.i. $f(\mathrm{i} u)$.
c.ii.g(iu).
d. Hence find, and simplify, an expression for $(f(\mathrm{iu}))^2+(g(\mathrm{iu}))^2$.
e. Show that $(f(t))^2-(g(t))^2=(f(\mathrm{i} u))^2-(g(\mathrm{i} u))^2$.
f. Sketch the graph of $x^2-y^2=1$, stating the coordinates of any axis intercepts and the equation of each asymptote.
g. The hyperbola with equation $x^2-y^2=1$ can be rotated to coincide with the curve defined by $x y=k, k \in \mathbb{R}$.
Find the possible values of $k$.
▶️Answer/Explanation
Markscheme
a. $f(t)=\frac{\mathrm{e}^t-\mathrm{e}^{-t}}{2}$
A1
$f^{\prime \prime}(t)=\frac{\mathrm{e}^t+\mathrm{e}^{-t}}{2}$
A1
$=f(t)$
AG
[2 marks]
b. METHOD 1
$(f(t))^2+(g(t))^2$
substituting $f$ and $g$
M1
$$
\begin{aligned}
& =\frac{\left(\mathrm{e}^t+\mathrm{e}^{-t}\right)^2+\left(\mathrm{e}^t-\mathrm{e}^{-t}\right)^2}{4} \\
& =\frac{\left(\mathrm{e}^t\right)^2+2+\left(\mathrm{e}^{-t}\right)^2+\left(\mathrm{e}^t\right)^2-2+\left(\mathrm{e}^{-t}\right)^2}{4} \\
& =\frac{\left(\mathrm{e}^t\right)^2+\left(\mathrm{e}^{-t}\right)^2}{2}\left(=\frac{\mathrm{e}^{2 t}+\mathrm{e}^{-2 t}}{2}\right) \\
& =f(2 t) \quad \boldsymbol{A G}
\end{aligned}
$$
AG
(M1)
A1
METHOD 2
$$
\begin{aligned}
& f(2 t)=\frac{\mathrm{e}^{2 t}+\mathrm{e}^{-2 t}}{2} \\
& =\frac{\left(\mathrm{e}^t\right)^2+\left(\mathrm{e}^{-t}\right)^2}{2} \quad \text { M1 } \\
& =\frac{\left(\mathrm{e}^t+\mathrm{e}^{-t}\right)^2+\left(\mathrm{e}^t-\mathrm{e}^{-t}\right)^2}{4} \\
& =(f(t))^2+(g(t))^2 \quad \text { MIA1 }
\end{aligned}
$$
Note: Accept combinations of METHODS 1 \& 2 that meet at equivalent expressions.
[3 marks]
c.i. substituting $\mathrm{e}^{\mathrm{i} u}=\cos u+\mathrm{i} \sin u$ into the expression for $f$
(M1)
obtaining $\mathrm{e}^{-\mathrm{i} u}=\cos u-\mathrm{i} \sin u$
(A1)
$f(\mathrm{i} u)=\frac{\cos u+\mathrm{i} \sin u+\cos u-\mathrm{i} \sin u}{2}$
Note: The $\boldsymbol{M} 1$ can be awarded for the use of sine and cosine being odd and even respectively.
$$
\begin{aligned}
& =\frac{2 \cos u}{2} \\
& =\cos u
\end{aligned}
$$
A1
[3 marks]
$$
\text { c.ii. } g(i u)=\frac{\cos u+i \sin u-\cos u+i \sin u}{2}
$$
substituting and attempt to simplify
(M1)
$$
\begin{aligned}
& =\frac{2 i \sin u}{2} \\
& =\mathrm{i} \sin u
\end{aligned}
$$
A1
[2 marks]
d. METHOD 1
$$
(f(\mathrm{i} u))^2+(g(\mathrm{i} u))^2
$$
substituting expressions found in part (c)
(M1)
$$
=\cos ^2 u-\sin ^2 u(=\cos 2 u)
$$
A1
METHOD 2
$$
\begin{aligned}
& f(2 \mathrm{i} u)=\frac{\mathrm{e}^{2 \mathrm{i} u}+\mathrm{e}^{-2 \mathrm{i} u}}{2} \\
& =\frac{\cos 2 u+\mathrm{i} \sin 2 u+\cos 2 u-\mathrm{i} \sin 2 u}{2} \\
& =\cos 2 u \quad \boldsymbol{A 1}
\end{aligned}
$$
A1
$M 1$
Note: Accept equivalent final answers that have been simplified removing all imaginary parts eg $2 \cos ^2 u-1$ etc
[2 marks]
e.
$(f(t))^2-(g(t))^2=\frac{\left(e^t+\mathrm{e}^{-t}\right)^2-\left(\mathrm{e}^t-\mathrm{e}^{-t}\right)^2}{4} \quad \boldsymbol{M 1}$
$$
\begin{aligned}
& =\frac{\left(\mathrm{e}^{2 t}+\mathrm{e}^{-2 t}+2\right)-\left(\mathrm{e}^{2 t}+\mathrm{e}^{-2 t}-2\right)}{4} \\
& =\frac{4}{4}=1 \quad \text { A1 }
\end{aligned}
$$
A1
A1
Note: Award $\boldsymbol{A} 1$ for a value of 1 obtained from either LHS or RHS of given expression.
$$
\begin{array}{ll}
(f(\mathrm{i} u))^2-(g(\mathrm{i} u))^2=\cos ^2 u+\sin ^2 u & \text { M1 } \\
=1\left(\text { hence }(f(t))^2-(g(t))^2=(f(\mathrm{i} u))^2-(g(\mathrm{i} u))^2\right) & \text { AG }
\end{array}
$$
Note: Award full marks for showing that $(f(z))^2-(g(z))^2=1, \forall z \in \mathbb{C}$.
[4 marks]
f.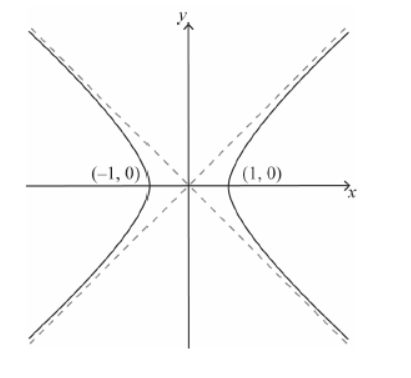
Note: Award $\boldsymbol{A} \boldsymbol{1}$ for correct curves in the upper quadrants, $\boldsymbol{A} \boldsymbol{1}$ for correct curves in the lower quadrants, $\boldsymbol{A} \boldsymbol{1}$ for correct $x$-intercepts of ( -1 , 0 ) and $(1,0)$ (condone $x=-1$ and 1 ), $\boldsymbol{A} 1$ for $y=x$ and $y=-x$.
[4 marks]
g. attempt to rotate by $45^{\circ}$ in either direction
(M1)
Note: Evidence of an attempt to relate to a sketch of $x y=k$ would be sufficient for this (M1).
attempting to rotate a particular point, eg $(1,0)$
(M1)
$(1,0)$ rotates to $\left(\frac{1}{\sqrt{2}}, \pm \frac{1}{\sqrt{2}}\right)$ (or similar)
(A1)
hence $k= \pm \frac{1}{2}$
A1A1
[5 marks]
Question
This question asks you to investigate and prove a geometric property involving the roots of the equation $z^n=1$ where $z \in \mathbb{C}$ for integers $n$, where $n \geq 2$.
The roots of the equation $z^n=\mathbf{1}$ where $\boldsymbol{z} \in \mathbb{C}$ are $1, \omega, \omega^2, \ldots, \omega^{n-1}$, where $\omega=\mathrm{e} \frac{2 \pi i}{n}$. Each root can be represented by a point $\mathrm{P}_0, \mathrm{P}_1, \mathrm{P}_2, \ldots, \mathrm{P}_{n-1}$, respectively, on an Argand diagram.
For example, the roots of the equation $z^2=1$ where $z \in \mathbb{C}$ are 1 and $\omega$. On an Argand diagram, the root 1 can be represented by a point $\mathrm{P}_0$ and the root $\omega$ can be represented by a point $P_1$.
Consider the case where $n=3$.
The roots of the equation $z^3=1$ where $z \in \mathbb{C}$ are $1, \omega$ and $\omega^2$. On the following Argand diagram, the points $\mathrm{P}_0, \mathrm{P}_1$ and $\mathrm{P}_2$ lie on a circle of radius 1 unit with centre $\mathrm{O}(0,0)$.
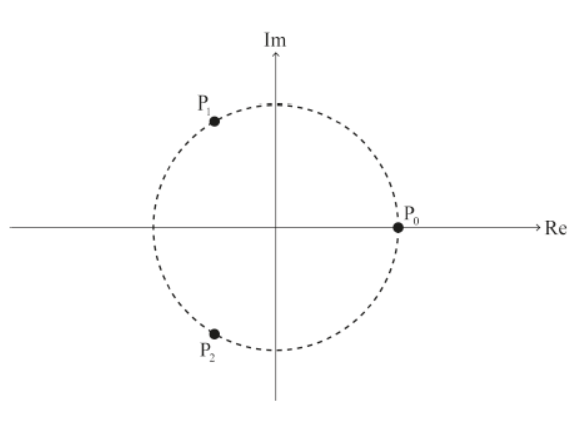
\text { Line segments }\left[\mathrm{P}_0 \mathrm{P}_1\right] \text { and }\left[\mathrm{P}_0 \mathrm{P}_2\right] \text { are added to the Argand diagram in part (a) and are shown on the following Argand diagram. }
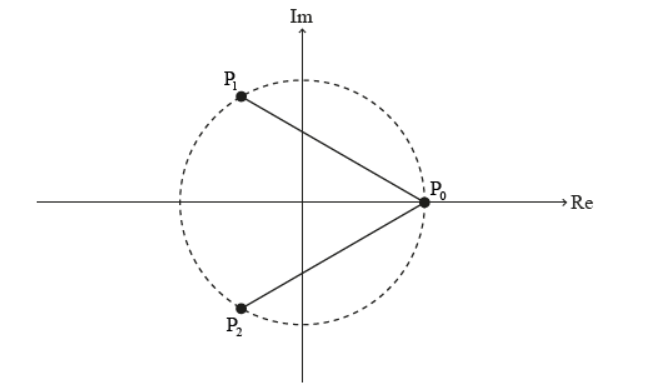
$\mathrm{P}_0 \mathrm{P}_1$ is the length of $\left[\mathrm{P}_0 \mathrm{P}_1\right]$ and $\mathrm{P}_0 \mathrm{P}_2$ is the length of $\left[\mathrm{P}_0 \mathrm{P}_2\right]$.
Consider the case where $n=4$
The roots of the equation $z^4=1$ where $z \in \mathbb{C}$ are $1, \omega, \omega^2$ and $\omega^3$.
On the following Argand diagram, the points $\mathrm{P}_0, \mathrm{P}_1, \mathrm{P}_2$ and $\mathrm{P}_3$ lie on a circle of radius 1 unit with centre $\mathrm{O}(0,0) .\left[\mathrm{P}_0 \mathrm{P}_1\right],\left[\mathrm{P}_0 \mathrm{P}_2\right]$ and $\left[\mathrm{P}_0 \mathrm{P}_3\right]$ are line segments.
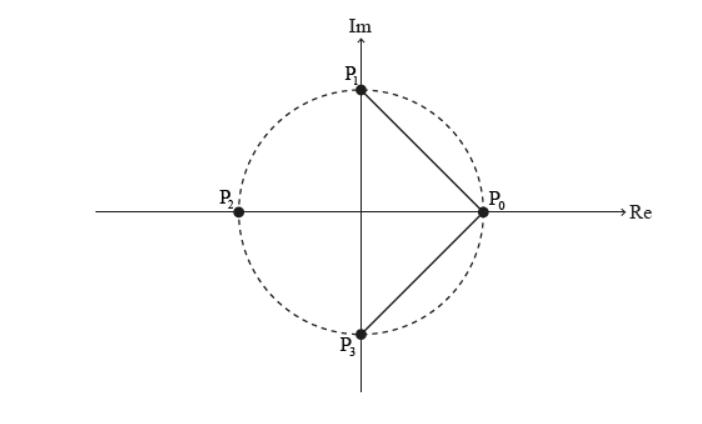
For the case where $n=5$, the equation $z^5=1$ where $z \in \mathbb{C}$ has roots $1, \omega, \omega^2, \omega^3$ and $\omega^4$.
It can be shown that $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2 \times \mathrm{P}_0 \mathrm{P}_3 \times \mathrm{P}_0 \mathrm{P}_4=5$.
Now consider the general case for integer values of $n$, where $n \geq 2$.
The roots of the equation $z^n=1$ where $z \in \mathbb{C}$ are $1, \omega, \omega^2, \ldots, \omega^{n-1}$. On an Argand diagram, these roots can be represented by the points $\mathrm{P}_0, \mathrm{P}_1, \mathrm{P}_2, \ldots, \mathrm{P}_{n-1}$ respectively where $\left[\mathrm{P}_0 \mathrm{P}_1\right],\left[\mathrm{P}_0 \mathrm{P}_2\right], \ldots,\left[\mathrm{P}_0 \mathrm{P}_{n-1}\right]$ are line segments. The roots lie on a circle of radius 1 unit with centre $\mathrm{O}(0,0)$.
$\mathrm{P}_0 \mathrm{P}_1$ can be expressed as $|1-\omega|$.
Consider $z^n-1=(z-1)\left(z^{n-1}+z^{n-2}+\ldots+z+1\right)$ where $z \in \mathbb{C}$.
a.i. Show that $(\omega-1)\left(\omega^2+\omega+1\right)=\omega^3-1$
a.ii. Hence, deduce that $\omega^2+\omega+1=0$.
b. Show that $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2=3$.
c. By factorizing $z^4-1$, or otherwise, deduce that $\omega^3+\omega^2+\omega+1=0$.
d. Show that $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2 \times \mathrm{P}_0 \mathrm{P}_3=4$.
e. Suggest a value for $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2 \times \ldots \times \mathrm{P}_0 \mathrm{P}_{n-1}$.
f.i. Write down expressions for $\mathrm{P}_0 \mathrm{P}_2$ and $\mathrm{P}_0 \mathrm{P}_3$ in terms of $\omega$.
[2]
f.ii. Hence, write down an expression for $\mathrm{P}_0 \mathrm{P}_{n-1}$ in terms of $n$ and $\omega$.
g.i. Express $z^{n-1}+z^{n-2}+\ldots+z+1$ as a product of linear factors over the set $\mathbb{C}$.
[3]
g.ii.Hence, using the part (g)(i) and part (f) results, or otherwise, prove your suggested result to part (e).
$[4]$
▶️Answer/Explanation
Markscheme
a.i. METHOD 1
attempts to expand $(\omega-1)\left(\omega^2+\omega+1\right)$
(M1)
$$
\begin{aligned}
& =\omega^3+\omega^2+\omega-\omega^2-\omega-1 \\
& =\omega^3-1 \quad \text { AG }
\end{aligned}
$$
A1
METHOD 2
attempts polynomial division on $\frac{\omega^3-1}{\omega-1} \quad \boldsymbol{M 1}$
$$
\begin{aligned}
& =\omega^2+\omega+1 \quad \text { A1 } \\
& \text { so }(\omega-1)\left(\omega^2+\omega+1\right)=\omega^3-1 \quad \text { AG }
\end{aligned}
$$
Note: In part (a), award marks as appropriate where $\omega$ has been converted into Cartesian, modulus-argument (polar) or Euler form.
[2 marks]
a.ii. (since $\omega$ is a root of $\left.z^3=1\right) \Rightarrow \omega^3-1=0 \quad \boldsymbol{R} 1$
$$
\begin{aligned}
& \text { and } \omega \neq 1 \quad \text { R1 } \\
& \Rightarrow \omega^2+\omega+1=0 \quad \text { AG }
\end{aligned}
$$
Note: In part (a), award marks as appropriate where $\omega$ has been converted into Cartesian, modulus-argument (polar) or Euler form.
[2 marks]
b. METHOD 1
attempts to find either $\mathrm{P}_0 \mathrm{P}_1$ or $\mathrm{P}_0 \mathrm{P}_2$
(M1)
accept any valid method
e.g. $2 \sin \frac{\pi}{3}, 1^2+1^2-2 \cos \frac{2 \pi}{3}, \frac{1}{\sin \frac{\pi}{6}}=\frac{\mathrm{P}_0 \mathrm{P}_1}{\sin \frac{2 \pi}{3}}$ from either $\Delta \mathrm{OP}_0 \mathrm{P}_1$ or $\Delta \mathrm{OP}_0 \mathrm{P}_2$
e.g. use of Pythagoras’ theorem
e.g. $\left|1-\mathrm{e}^{\frac{2 \pi}{3}}\right|,\left|1-\left(-\frac{1}{2}+\frac{\sqrt{3}}{2} \mathrm{i}\right)\right|$ by calculating the distance between 2 points
$$
\begin{aligned}
& \mathrm{P}_0 \mathrm{P}_1=\sqrt{3} \\
& \mathrm{P}_0 \mathrm{P}_2=\sqrt{3}
\end{aligned}
$$
A1
$\mathrm{P}_0 \mathrm{P}_2=\sqrt{3}$
A1
Note: Award a maximum of M1A1AO for any decimal approximation seen in the calculation of either $\mathrm{P}_0 \mathrm{P}_1$ or $\mathrm{P}_0 \mathrm{P}_2$ or both.
so $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2=3 \quad \boldsymbol{A G}$
METHOD 2
attempts to find $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2=|1-\omega|\left|1-\omega^2\right|$
(M1)
$$
\begin{aligned}
& \mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2=\left|\omega^3-\omega^2-\omega+1\right| \quad \text { A1 } \\
& =\left|1-\left(\omega^2+\omega+1\right)+2\right| \text { and since } \omega^2+\omega+1=0 \\
& \text { so } \mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2=3 \quad \text { AG }
\end{aligned}
$$
[ 3 marks]
c. METHOD 1
$$
\begin{aligned}
& z^4-1=(z-1)\left(z^3+z^2+z+1\right) \quad \text { A1 } \\
& (\omega \text { is a root hence }) \omega^4-1=0 \text { and } \omega \neq 1 \quad \text { R1 } \\
& \Rightarrow \omega^3+\omega^2+\omega+1=0 \quad \text { AG }
\end{aligned}
$$
Note: Condone the use of $\omega$ throughout.
METHOD 2
considers the sum of roots of $z^4-1=0$
the sum of roots is zero (there is no $z^3$ term)
$\Rightarrow \omega^3+\omega^2+\omega+1=0$
(M1)
A1
METHOD 3
substitutes for $\omega$
(M1)
e.g. $\mathrm{LHS}=\mathrm{e}^{\mathrm{i} \frac{3 \pi}{2}}+\mathrm{e}^{\pi \mathrm{i}}+\mathrm{e}^{\mathrm{i} \frac{\pi}{2}}+1$
$=-i-1+i+1$
A1
Note: This can be demonstrated geometrically or by using vectors. Accept Cartesian or modulus-argument (polar) form.
$$
\Rightarrow \omega^3+\omega^2+\omega+1=0 \quad \boldsymbol{A G}
$$
METHOD 4
$$
\begin{aligned}
& \omega^3+\omega^2+\omega+1=\frac{\omega^4-1}{\omega-1} \quad \text { A1 } \\
& =\frac{0}{\omega-1}=0 \text { as } \omega \neq 1 \quad \boldsymbol{R T} \\
& \Rightarrow \omega^3+\omega^2+\omega+1=0 \quad \text { AG }
\end{aligned}
$$
A1
AG
[2 marks]
d. METHOD 1
$\mathrm{P}_0 \mathrm{P}_2=2$
A1
attempts to find either $\mathrm{P}_0 \mathrm{P}_1$ or $\mathrm{P}_0 \mathrm{P}_3$
(M1)
Note: For example $\mathrm{P}_0 \mathrm{P}_1=|1-\mathrm{i}|$ and $\mathrm{P}_0 \mathrm{P}_3=|1+\mathrm{i}|$.
Various geometric and trigonometric approaches can be used by candidates.
$\mathrm{P}_0 \mathrm{P}_1=\sqrt{2}, \mathrm{P}_0 \mathrm{P}_3=\sqrt{2}$
$A 1 A 1$
Note: Award a maximum of $A 1 M 1 A 1 A O$ if labels such as $\mathrm{P}_0 \mathrm{P}_1$ are not clearly shown.
Award full marks if the lengths are shown on a clearly labelled diagram.
Award a maximum of A1M1A1AO for any decimal approximation seen in the calculation of either $\mathrm{P}_0 \mathrm{P}_1$ or $\mathrm{P}_0 \mathrm{P}_3$ or both.
$$
\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2 \times \mathrm{P}_0 \mathrm{P}_3=4 \quad \text { AG }
$$
METHOD 2
attempts to find $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2 \times \mathrm{P}_0 \mathrm{P}_3=|1-\omega|\left|1-\omega^2\right|\left|1-\omega^3\right| \quad$ M1
$$
\begin{aligned}
& \mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2 \times \mathrm{P}_0 \mathrm{P}_3=\left|-\omega^6+\omega^5+\omega^4-\omega^2-\omega+1\right| \quad \text { A1 } \\
& =\left|-(-1)+\omega^5+1-(-1)-\omega+1\right| \text { since } \omega^6=\omega^2=-1 \text { and } \omega^4=1 \\
& =\left|\omega^5-\omega+4\right| \text { and since } \omega^5=\omega \quad \text { R1 } \\
& \text { so } \mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2 \times \mathrm{P}_0 \mathrm{P}_3=4 \quad \text { AG }
\end{aligned}
$$
A1
METHOD 3
$$
\mathrm{P}_0 \mathrm{P}_2=2
$$
A1
attempts to find $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_3=|1-\omega|\left|1-\omega^3\right| \quad$ M1
$$
\begin{aligned}
& \mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_3=\left|\omega^4-\omega^3-\omega+1\right| \quad \text { A1 } \\
& =|2-(-\omega)-\omega| \text { since } \omega^4=1 \text { and } \omega^3=-\omega \quad \text { R1 } \\
& \text { so } \mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2 \times \mathrm{P}_0 \mathrm{P}_3=4 \quad \text { AG }
\end{aligned}
$$
[4 marks]
e. $\left(\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2 \times \ldots \times \mathrm{P}_0 \mathrm{P}_{n-1}\right)=n$
A1
[1 mark]
f.i. $\mathrm{P}_0 \mathrm{P}_2=\left|1-\omega^2\right|, \mathrm{P}_0 \mathrm{P}_3=\left|1-\omega^3\right| \quad$ A1A1
[2 marks]
f.ii. $\mathrm{P}_0 \mathrm{P}_{n-1}=\left|1-\omega^{n-1}\right| \quad$ A1A1
Note: Accept $|1-\omega|$ from symmetry.
[1 mark]
g.i. $z^n-1=(z-1)\left(z^{n-1}+z^{n-2}+\ldots+z+1\right)$
considers the equation $z^{n-1}+z^{n-2}+\ldots+z+1=0$
(M1)
the roots are $\omega, \omega^2, \ldots, \omega^{n-1}$
(A1)
So $(z-\omega)\left(z-\omega^2\right) \ldots\left(z-\omega^{n-1}\right)$
A1
[3 marks]
g.iiMETHOD 1
substitutes $z=1$ into $(z-\omega)\left(z-\omega^2\right) \ldots\left(z-\omega^{n-1}\right) \equiv z^{n-1}+z^{n-2}+\ldots+z+1 \quad$ M1
$$
(1-\omega)\left(1-\omega^2\right) \ldots\left(1-\omega^{n-1}\right)=n
$$
takes modulus of both sides $\quad$ M1
$$
\begin{aligned}
& \left|(1-\omega)\left(1-\omega^2\right) \ldots\left(1-\omega^{n-1}\right)\right|=|n| \\
& |1-\omega|\left|1-\omega^2\right| \ldots\left|1-\omega^{n-1}\right|=n \\
& \operatorname{so~}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2 \times \ldots \times \mathrm{P}_0 \mathrm{P}_{n-1}=n \quad \text { A1 } \quad \text { AG }
\end{aligned}
$$
A1
AG
Note: Award a maximum of M1A1FTM1AO from part (e).
METHOD 2
$(1-\omega),\left(1-\omega^2\right), \ldots,\left(1-\omega^{n-1}\right)$ are the roots of $(1-v)^{n-1}+(1-v)^{n-2}+\ldots+(1-v)+1=0 \quad \boldsymbol{M 1}$ coefficient of $v^{n-1}$ is $(-1)^{n-1}$ and the coefficient of 1 is $n$
41 product of the roots is $\frac{(-1)^{n-1} n}{(-1)^{n-1}}=n$
A1
$|1-\omega|\left|1-\omega^2\right| \cdots\left|1-\omega^{n-1}\right|=n$
A1 so $\mathrm{P}_0 \mathrm{P}_1 \times \mathrm{P}_0 \mathrm{P}_2 \times \ldots \times \mathrm{P}_0 \mathrm{P}_{n-1}=n$
AG
[4 marks]
Question
Question
In this question you will explore some of the properties of special functions $f$ and $g$ and their relationship with the trigonometric functions, sine and cosine.
Functions $f$ and $g$ are defined as $f(z)=\frac{\mathrm{e}^z+\mathrm{e}^{-z}}{2}$ and $g(z)=\frac{\mathrm{e}^z-\mathrm{e}^{-z}}{2}$, where $z \in \mathbb{C}$.
Consider $t$ and $u$, such that $t, u \in \mathbb{R}$.
Using $\mathrm{e}^{\mathrm{i} u}=\cos u+\mathrm{i} \sin u$, find expressions, in terms of $\sin u$ and $\cos u$, for
The functions $\cos x$ and $\sin x$ are known as circular functions as the general point $(\cos \theta, \sin \theta)$ defines points on the unit circle with equation $x^2+y^2=1$. The functions $f(x)$ and $g(x)$ are known as hyperbolic functions, as the general point $(f(\theta), g(\theta))$ defines points on a curve known as a hyperbola with equation $x^2-y^2=1$. This hyperbola has two asymptotes.
a. Verify that $u=f(t)$ satisfies the differential equation $\frac{d^2 u}{d t^2}=u$.
[5]
b. Show that $(f(t))^2+(g(t))^2=f(2 t)$.
c.i. $f(\mathrm{i} i)$.
[3]
c.ii.g(iu).
[2]
d. Hence find, and simplify, an expression for $(f(\mathrm{i} u))^2+(g(\mathrm{i} u))^2$.
[2]
e. Show that $(f(t))^2-(g(t))^2=(f(1 u))^2-(g(1 u))^2$.
f. Sketch the graph of $x^2-y^2=1$, stating the coordinates of any axis intercepts and the equation of each asymptote.
g. The hyperbola with equation $x^2-y^2=1$ can be rotated to coincide with the curve defined by $x y=k, k \in \mathbb{R}$. Find the possible values of $k$.
▶️Answer/Explanation
Markscheme
a. $f(t)=\frac{\mathrm{e}^t-\mathrm{e}^{-t}}{2}$
A1
$$
\begin{array}{ll}
f^{\prime \prime}(t)=\frac{\mathrm{e}^t+\mathrm{e}^{-t}}{2} & \\
=f(t) \quad \text { AG }
\end{array}
$$
A1
[2 marks]
b. METHOD 1
$$
(f(t))^2+(g(t))^2
$$
substituting $f$ and $g$
M1
$$
\begin{aligned}
& =\frac{\left(\mathrm{e}^t+\mathrm{e}^{-t}\right)^2+\left(\mathrm{e}^t-\mathrm{e}^{-t}\right)^2}{4} \\
& =\frac{\left(\mathrm{e}^t\right)^2+2+\left(\mathrm{e}^{-t}\right)^2+\left(\mathrm{e}^t\right)^2-2+\left(\mathrm{e}^{-t}\right)^2}{4} \\
& =\frac{\left(\mathrm{e}^t\right)^2+\left(\mathrm{e}^{-t}\right)^2}{2}\left(=\frac{\mathrm{e}^{2 t}+\mathrm{e}^{-2 t}}{2}\right) \\
& =f(2 t) \quad \boldsymbol{A G}
\end{aligned}
$$
(M1)
A1
METHOD 2
$$
\begin{aligned}
& f(2 t)=\frac{\mathrm{e}^{2 t}+\mathrm{e}^{-2 t}}{2} \\
& =\frac{\left(\mathrm{e}^t\right)^2+\left(\mathrm{e}^{-t}\right)^2}{2} \quad \text { M1 } \\
& =\frac{\left(\mathrm{e}^t+\mathrm{e}^{-t}\right)^2+\left(\mathrm{e}^t-\mathrm{e}^{-t}\right)^2}{4} \quad \text { M1A1 } \\
& =(f(t))^2+(g(t))^2
\end{aligned}
$$
Note: Accept combinations of METHODS 1 \& 2 that meet at equivalent expressions.
[3 marks]
c.i. substituting $\mathrm{e}^{\mathrm{i} u}=\cos u+\mathrm{i} \sin u$ into the expression for $f$
(M1)
obtaining $\mathrm{e}^{-\mathrm{i} u}=\cos u-\mathrm{i} \sin u$
(A1)
$$
f(\mathrm{i} u)=\frac{\cos u+\mathrm{i} \sin u+\cos u-\mathrm{i} \sin u}{2}
$$
Note: The $\boldsymbol{M} 1$ can be awarded for the use of sine and cosine being odd and even respectively.
$$
\begin{aligned}
& =\frac{2 \cos u}{2} \\
& =\cos u
\end{aligned}
$$
A1
[3 marks]
$$
\text { c.iig } g(i u)=\frac{\cos u+i \sin u-\cos u+i \sin u}{2}
$$
substituting and attempt to simplify
(M1)
$$
\begin{aligned}
& =\frac{2 \mathrm{i} \sin u}{2} \\
& =\mathrm{i} \sin u
\end{aligned}
$$
A1
[2 marks]
d. METHOD 1
$\left(f(\mathrm{i} u)^2+\left(g(\mathrm{i} u)^2\right.\right.$
substituting expressions found in part (c)
(M1)
$=\cos ^2 u-\sin ^2 u(=\cos 2 u)$
A1
METHOD 2
$$
\begin{aligned}
& f(2 \mathrm{i} u)=\frac{\mathrm{e}^{2 \mathrm{iu}}+\mathrm{e}^{-2 \mathrm{i} u}}{2} \\
& =\frac{\cos 2 u+\mathrm{i} \sin 2 u+\cos 2 u-\mathrm{i} \sin 2 u}{2} \\
& =\cos 2 u \quad \boldsymbol{A 1}
\end{aligned}
$$
A1
M1
Note: Accept equivalent final answers that have been simplified removing all imaginary parts eg $2 \cos ^2 u-1$ etc
[2 marks]
e.
$$
\begin{aligned}
& (f(t))^2-(g(t))^2=\frac{\left(\mathrm{e}^t+\mathrm{e}^{-t}\right)^2-\left(\mathrm{e}^t-\mathrm{e}^{-t}\right)^2}{4} \\
& =\frac{\left(\mathrm{e}^{2 t}+\mathrm{e}^{-2 t}+2\right)-\left(\mathrm{e}^{2 t}+\mathrm{e}^{-2 t}-2\right)}{4} \quad \text { M1 } \\
& =\frac{4}{4}=1 \quad \text { A1 }
\end{aligned}
$$
A1
A1
Note: Award $\boldsymbol{A} 1$ for a value of 1 obtained from either LHS or RHS of given expression.
$$
\begin{aligned}
& (f(\mathrm{i} u))^2-(g(\mathrm{i} u))^2=\cos ^2 u+\sin ^2 u \quad \text { M1 } \\
& =1\left(\text { hence }(f(t))^2-(g(t))^2=(f(\mathrm{i} u))^2-(g(\mathrm{i} u))^2\right) \quad \boldsymbol{A G} \\
&
\end{aligned}
$$
Note: Award full marks for showing that $(f(z))^2-(g(z))^2=1, \forall z \in \mathbb{C}$.
[4 marks]
f.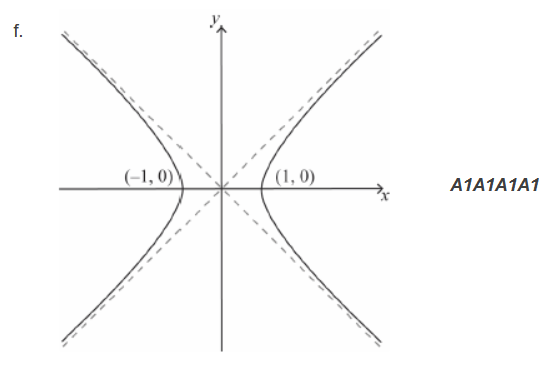
Note: Award $\boldsymbol{A} \mathbf{1}$ for correct curves in the upper quadrants, $\boldsymbol{A} \boldsymbol{1}$ for correct curves in the lower quadrants, $\boldsymbol{A} \boldsymbol{1}$ for correct $x$-intercepts of ( $-1,0$ ) and $(1,0)$ (condone $x=-1$ and 1), $\boldsymbol{A 1}$ for $y=x$ and $y=-x$.
[4 marks]
g. attempt to rotate by $45^{\circ}$ in either direction
(M1)
Note: Evidence of an attempt to relate to a sketch of $x y=k$ would be sufficient for this (M1).
attempting to rotate a particular point, eg $(1,0)$
(M1)
$(1,0)$ rotates to $\left(\frac{1}{\sqrt{2}}, \pm \frac{1}{\sqrt{2}}\right)$ (or similar)
(A1)
hence $k= \pm \frac{1}{2}$
A1A1
[5 marks]
Question
This question will explore connections between complex numbers and regular polygons.
The diagram below shows a sector of a circle of radius 1, with the angle subtended at the centre $O$ being $\alpha, 0<\alpha<\frac{\pi}{2}$. A perpendicular is drawn from point $P$ to intersect the $x$-axis at $Q$. The tangent to the circle at $P$ intersects the $x$-axis at $R$.

a. By considering the area of two triangles and the area of the sector show that $\cos \alpha \sin \alpha<\alpha<\frac{\sin \alpha}{\cos \alpha}$.
b. Hence show that $\lim _{\alpha \rightarrow 0} \frac{\alpha}{\sin \alpha}=1$.
c. Let $z^n=1, z \in \mathbb{C}, n \in \mathbb{N}, n \geqslant 5$. Working in modulus/argument form find the $n$ solutions to this equation.
d. Represent these $n$ solutions on an Argand diagram. Let their positions be denoted by $P_0, P_1, P_2, \ldots P_{n-1}$ placed in order in an anticlockwise direction round the circle, starting on the positive $x$-axis. Show the positions of $P_0, P_1, P_2$ and $P_{n-1}$.
e. Show that the length of the line segment $P_0 P_1$ is $2 \sin \frac{\pi}{n}$.
f. Hence, write down the total length of the perimeter of the regular $n$ sided polygon $P_0 P_1 P_2 \ldots P_{n-1} P_0$.
g. Using part (b) find the limit of this perimeter as $n \rightarrow \infty$.
h. Find the total area of this $n$ sided polygon.
i. Using part (b) find the limit of this area as $n \rightarrow \infty$.
▶️Answer/Explanation
a. Area triangle $O P Q=\frac{1}{2} \cos \alpha \sin \alpha$
A1
Area sector $=\frac{1}{2} 1^2 \alpha$
A1
Area triangle $O P R=\frac{1}{2} 1 \tan \alpha$
A1
So looking at the diagram $\frac{1}{2} \cos \alpha \sin \alpha<\frac{1}{2} \alpha<\frac{1}{2} \frac{\sin \alpha}{\cos \alpha} \quad$ M1
$\Rightarrow \cos \alpha \sin \alpha<\alpha<\frac{\sin \alpha}{\cos \alpha} \quad$ AG
[5 marks]
b. Hence $\cos \alpha<\frac{\alpha}{\sin \alpha}<\frac{1}{\cos \alpha}$ and as $\alpha \rightarrow 0, \cos \alpha \rightarrow 1$ we have M1R1 $\lim _{\alpha \rightarrow 0} \frac{\alpha}{\sin \alpha}=1 \quad \boldsymbol{A G}$
[2 marks]
c.
$$
\begin{aligned}
& (r \operatorname{cis} \theta)^n=1 \text { cis } 0 \Rightarrow r^n \operatorname{cis} n \theta=1 \operatorname{cis} \theta \\
& r^n=1 \Rightarrow r=1 \quad n \theta=0+2 \pi k, k \in \mathbb{Z} \\
& \theta=\frac{2 \pi k}{n}, 0 \leqslant k \leqslant n-1 \quad \text { A1 } \\
& z=\operatorname{cis} \frac{2 \pi k}{n}, 0 \leqslant k \leqslant n-1 \quad \text { A1 }
\end{aligned}
$$
M1A1M1A1
A1A1
[8 marks]
A1
d.
e. Bisecting the triangle $O P_0 P_1$ to form two right angle triangles

Length of $P_0 P_1=2 t$ where $t=\sin \left(\frac{\frac{2 \pi}{n}}{2}\right) \quad$ M1A1A1
So length is $2 \sin \frac{\pi}{n} \quad A G$
[4 marks]
f. Length of perimeter is $2 n \sin \frac{\pi}{n} \quad \boldsymbol{A 1}$
[1 mark]
g. $2 n \sin \frac{\pi}{n}=2 \pi \frac{n}{\pi} \sin \frac{\pi}{n} \rightarrow 2 \pi$ as $n \rightarrow \infty \quad$ M1A1
[2 marks]
h. Area of $O P_0 P_1=\frac{1}{2} 1 \times 1 \sin \frac{2 \pi}{n}$ so total area is $\frac{n}{2} \sin \frac{2 \pi}{n}$. M1A1A1
[3 marks]
i. $\frac{n}{2} \sin \frac{2 \pi}{n}=\pi \frac{n}{2 \pi} \sin \frac{2 \pi}{n} \rightarrow \pi$ as $n \rightarrow \infty \quad$ M1A1
[2 marks]
Question
A Gaussian integer is a complex number, $z$, such that $z=a+b \mathrm{i}$ where $a, b \in \mathbb{Z}$. In this question, you are asked to investigate certain divisibility properties of Gaussian integers.
Consider two Gaussian integers, $\alpha=3+4 \mathrm{i}$ and $\beta=1-2 \mathrm{i}$, such that $\gamma=\alpha \beta$ for some Gaussian integer $\gamma$.
Now consider two Gaussian integers, $\alpha=3+4 \mathrm{i}$ and $\gamma=11+2 \mathrm{i}$.
The norm of a complex number $z$, denoted by $N(z)$, is defined by $N(z)=|z|^2$. For example, if $z=2+3 \mathrm{i}$ then $N(2+3 \mathrm{i})=2^2+3^2=13$.
A Gaussian prime is a Gaussian integer, $z$, that cannot be expressed in the form $z=\alpha \beta$ where $\alpha, \beta$ are Gaussian integers with $N(\alpha), N(\beta)>1$.
The positive integer 2 is a prime number, however it is not a Gaussian prime.
Let $\alpha, \beta$ be Gaussian integers.
The result from part (h) provides a way of determining whether a Gaussian integer is a Gaussian prime.
a. Find $\gamma$.
b. Determine whether $\frac{\gamma}{\alpha}$ is a Gaussian integer.
c. On an Argand diagram, plot and label all Gaussian integers that have a norm less than 3 .
d. Given that $\alpha=a+b$ i where $a, b \in \mathbb{Z}$, show that $N(\alpha)=a^2+b^2$.
e. By expressing the positive integer $n=c^2+d^2$ as a product of two Gaussian integers each of norm $c^2+d^2$, show that $n$ is not a Gaussian prime.
f. Verify that 2 is not a Gaussian prime.
g. Write down another prime number of the form $c^2+d^2$ that is not a Gaussian prime and express it as a product of two Gaussian integers.
h. Show that $N(\alpha \beta)=N(\alpha) N(\beta)$.
i. Hence show that $1+4 \mathrm{i}$ is a Gaussian prime.
j. Use proof by contradiction to prove that a prime number, $p$, that is not of the form $a^2+b^2$ is a Gaussian prime.
▶️Answer/Explanation
a.$(3+4 i)(1-2 i)=11-2 i$
(M1)A1
[2 marks]
b. $\frac{\gamma}{\alpha}=\frac{41}{25}-\frac{38}{25} \mathrm{i} \quad$ (M1)A1
(Since $\operatorname{Re} \frac{\gamma}{\alpha}\left(=\frac{41}{25}\right)$ and/or $\operatorname{Im} \frac{\gamma}{\alpha}\left(=-\frac{38}{25}\right)$ are not integers) $\frac{\gamma}{\alpha}$ is not a Gaussian integer $\quad \boldsymbol{R 1}$
Note: Award R1 for correct conclusion from their answer.
[3 marks]
c. $\pm 1, \pm \mathrm{i}, 0$ plotted and labelled
A1
$1 \pm \mathrm{i},-1 \pm \mathrm{i}$ plotted and labelled
A1
Note: Award A1AO if extra points to the above are plotted and labelled.
[2 marks]
d. $|z|=\sqrt{a^2+b^2}$ (and as $N(z)=|z|^2$ )
A1
then $N(\alpha)=a^2+b^2 \quad A G$
[1 mark]
e. $c^2+d^2=(c+d \mathrm{i})(c-d \mathrm{i})$
A1
and $N(c+d \mathrm{i})=N(c-d \mathrm{i})=c^2+d^2$
R1
$N(c+d \mathrm{i}), N(c-d \mathrm{i})>1$ (since $c, d$ are positive)
R1
so $c^2+d^2$ is not a Gaussian prime, by definition
AG
[3 marks]
f.
$$
\begin{aligned}
& 2\left(=1^2+1^2\right)=(1+\mathrm{i})(1-\mathrm{i}) \\
& N(1+\mathrm{i})=N(1-\mathrm{i})=2 \quad \text { A1 }
\end{aligned}
$$
so 2 is not a Gaussian prime
$A G$
[2 marks]
g. For example, $5\left(=1^2+2^2\right)=(1+2 \mathrm{i})(1-2 \mathrm{i})$
(M1)A1
h. METHOD 1
Let $\alpha=m+n \mathrm{i}$ and $\beta=p+q \mathrm{i}$
LHS:
$$
\begin{aligned}
& \alpha \beta=(m p-n q)+(m q+n p) \mathrm{i} \quad \text { M1 } \\
& N(\alpha \beta)=(m p-n q)^2+(m q+n p)^2 \\
& (m p)^2-2 m n p q+(n q)^2+(m q)^2+2 m n p q+(n p)^2 \\
& (m p)^2+(n q)^2+(m q)^2+(n p)^2
\end{aligned}
$$
RHS:
$$
\begin{aligned}
& N(\alpha) N(\beta)=\left(m^2+n^2\right)\left(p^2+q^2\right) \quad \text { M1 } \\
& (m p)^2+(m q)^2+(n p)^2+(n q)^2 \quad \text { A1 } \\
& \text { LHS }=\text { RHS and so } N(\alpha \beta)=N(\alpha) N(\beta) \quad \text { AG }
\end{aligned}
$$
A1
METHOD 2
Let $\alpha=m+n \mathrm{i}$ and $\beta=p+q \mathrm{i}$
LHS
$$
\begin{aligned}
& N(\alpha \beta)=\left(m^2+n^2\right)\left(p^2+q^2\right) \quad \text { M1 } \\
& =(m+n \mathrm{i})(m-n \mathrm{i})(p+q \mathrm{i})(p-q \mathrm{i}) \quad \text { A1 } \\
& =(m+n \mathrm{i})(p+q \mathrm{i})(m-n \mathrm{i})(p-q \mathrm{i}) \\
& =((m p-n q)+(m q+n p) \mathrm{i})((m p-n q)-(m q+n p) \mathrm{i}) \quad \text { M1A1 } \\
& =(m p-n q)^2+(m q+n p)^2 \quad \text { A1 } \\
& N=((m p-n q)+(m q+n p) \mathrm{i}) \quad \text { A1 } \\
& =N(\alpha) N(\beta) \text { (= RHS) } \quad \text { AG }
\end{aligned}
$$
[6 marks]
i. $N(1+4 \mathrm{i})=17$ which is a prime (in $\mathbb{Z}) \quad \boldsymbol{R} \mathbf{1}$
if $1+4 \mathrm{i}=\alpha \beta$ then $17=N(\alpha \beta)=N(\alpha) N(\beta) \quad \boldsymbol{R 1}$ we cannot have $N(\alpha), N(\beta)>1 \quad$ R1
Note: Award $\boldsymbol{R 1}$ for stating that $1+4 \mathrm{i}$ is not the product of Gaussian integers of smaller norm because no such norms divide 17
so $1+4 \mathrm{i}$ is a Gaussian prime
AG
[3 marks]
j. Assume $p$ is not a Gaussian prime
$\Rightarrow p=\alpha \beta$ where $\alpha, \beta$ are Gaussian integers and $N(\alpha), N(\beta)>1 \quad$ M1
$\Rightarrow N(p)=N(\alpha) N(\beta) \quad$ M1
$p^2=N(\alpha) N(\beta) \quad \boldsymbol{A 1}$
It cannot be $N(\alpha)=1, N(\beta)=p^2$ from definition of Gaussian prime
R1
hence $N(\alpha)=p, N(\beta)=p \quad \boldsymbol{R 1}$
If $\alpha=a+b \mathrm{i}$ then $N(\alpha)=a^2+b^2=p$ which is a contradiction $\quad \boldsymbol{R} \mathbf{1}$
hence a prime number, $p$, that is not of the form $a^2+b^2$ is a Gaussian prime
AG
[6 marks]