Question may 2022
This question asks you to investigate conditions for the existence of complex roots of polynomial equations of degree 3 and 4 .
The cubic equation $x^3+p x^2+q x+r=0$, where $p, q, r \in \mathbb{R}$, has roots $\alpha, \beta$ and $\gamma$.
Consider the equation $x^3-7 x^2+q x+1=0$, where $q \in \mathbb{R}$.
Noah believes that if $p^2 \geq 3 q$ then $\alpha, \beta$ and $\gamma$ are all real.
Now consider polynomial equations of degree 4 .
The equation $x^4+p x^3+q x^2+r x+s=0$, where $p, q, r, s \in \mathbb{R}$, has roots $\alpha, \beta, \gamma$ and $\delta$.
In a similar way to the cubic equation, it can be shown that:
$$
\begin{aligned}
& p=-(\alpha+\beta+\gamma+\delta) \\
& q=\alpha \beta+\alpha \gamma+\alpha \delta+\beta \gamma+\beta \delta+\gamma \delta \\
& r=-(\alpha \beta \gamma+\alpha \beta \delta+\alpha \gamma \delta+\beta \gamma \delta) \\
& s=\alpha \beta \gamma \delta .
\end{aligned}
$$
The equation $x^4-9 x^3+24 x^2+22 x-12=0$, has one integer root.
a. By expanding $(x-\alpha)(x-\beta)(x-\gamma)$ show that:
$$
\begin{aligned}
& p=-(\alpha+\beta+\gamma) \\
& q=\alpha \beta+\beta \gamma+\gamma \alpha \\
& r=-\alpha \beta \gamma .
\end{aligned}
$$
b.i. Show that $p^2-2 q=\alpha^2+\beta^2+\gamma^2$.
b.ii.Hence show that $(\alpha-\beta)^2+(\beta-\gamma)^2+(\gamma-\alpha)^2=2 p^2-6 q$
c. Given that $p^2<3 q$, deduce that $\alpha, \beta$ and $\gamma$ cannot all be real.
d. Using the result from part (c), show that when $q=17$, this equation has at least one complex root.
e.i. By varying the value of $q$ in the equation $x^3-7 x^2+q x+1=0$, determine the smallest positive integer value of $q$ required to show that Noah is incorrect.
e.ii.Explain why the equation will have at least one real root for all values of $q$.
[1]
f.i. Find an expression for $\alpha^2+\beta^2+\gamma^2+\delta^2$ in terms of $p$ and $q$.
f.ii. Hence state a condition in terms of $p$ and $q$ that would imply $x^4+p x^3+q x^2+r x+s=0$ has at least one complex root.
[1]
g. Use your result from part (f)(ii) to show that the equation $x^4-2 x^3+3 x^2-4 x+5=0$ has at least one complex root.
h.i. State what the result in part (f)(ii) tells us when considering this equation $x^4-9 x^3+24 x^2+22 x-12=0$.
[1]
h.ii.Write down the integer root of this equation.
h.iiiBy writing $x^4-9 x^3+24 x^2+22 x-12$ as a product of one linear and one cubic factor, prove that the equation has at least one complex root.
▶️Answer/Explanation
Markscheme
a. attempt to expand $(x-\alpha)(x-\beta)(x-\gamma) \quad$ M1
$$
\begin{array}{ll}
=\left(x^2-(\alpha+\beta) x+\alpha \beta\right)(x-\gamma) \text { OR }=(x-\alpha)\left(x^2-(\beta+\gamma) x+\beta \gamma\right) & \text { A1 } \\
\left(x^3+p x^2+q x+r\right)=x^3-(\alpha+\beta+\gamma) x^2+(\alpha \beta+\beta \gamma+\gamma \alpha) x-\alpha \beta \gamma \quad & \text { A1 }
\end{array}
$$
comparing coefficients:
$$
\begin{aligned}
& p=-(\alpha+\beta+\gamma) \quad \text { AG } \\
& q=(\alpha \beta+\beta \gamma+\gamma \alpha) \quad \text { AG } \\
& r=-\alpha \beta \gamma \quad \boldsymbol{A G}
\end{aligned}
$$
Note: For candidates who do not include the $\boldsymbol{A G}$ lines award full marks.
[3 marks]
b.i. $p^2-2 q=(\alpha+\beta+\gamma)^2-2(\alpha \beta+\beta \gamma+\gamma \alpha)$
(A1)
attempt to expand $(\alpha+\beta+\gamma)^2$
(M1)
$$
\begin{aligned}
& =\alpha^2+\beta^2+\gamma^2+2(\alpha \beta+\beta \gamma+\gamma \alpha)-2(\alpha \beta+\beta \gamma+\gamma \alpha) \text { or equivalent } \\
& =\alpha^2+\beta^2+\gamma^2 \quad \text { AG }
\end{aligned}
$$
AG
A1
Note: Accept equivalent working from RHS to LHS.
[3 marks]
b.ii.EITHER
attempt to expand $(\alpha-\beta)^2+(\beta-\gamma)^2+(\gamma-\alpha)^2$
(M1)
$$
\begin{aligned}
& =\left(\alpha^2+\beta^2-2 \alpha \beta\right)+\left(\beta^2+\gamma^2-2 \beta \gamma\right)+\left(\gamma^2+\alpha^2-2 \gamma \alpha\right) \\
& =2\left(\alpha^2+\beta^2+\gamma^2\right)-2(\alpha \beta+\beta \gamma+\gamma \alpha) \\
& =2\left(p^2-2 q\right)-2 q \text { or equivalent A1 } \\
& =2 p^2-6 q \quad \text { AG }
\end{aligned}
$$
A1
A1
OR
attempt to write $2 p^2-6 q$ in terms of $\alpha, \beta, \gamma$
(M1)
$$
\begin{aligned}
& =2\left(p^2-2 q\right)-2 q \\
& =2\left(\alpha^2+\beta^2+\gamma^2\right)-2(\alpha \beta+\beta \gamma+\gamma \alpha) \quad \text { A1 } \\
& =\left(\alpha^2+\beta^2-2 \alpha \beta\right)+\left(\beta^2+\gamma^2-2 \beta \gamma\right)+\left(\gamma^2+\alpha^2-2 \gamma \alpha\right) \\
& =(\alpha-\beta)^2+(\beta-\gamma)^2+(\gamma-\alpha)^2 \quad \text { AG }
\end{aligned}
$$
A1
A1
Note: Accept equivalent working where LHS and RHS are expanded to identical expressions.
[3 marks]
C.
$$
\begin{aligned}
& p^2<3 q \Rightarrow 2 p^2-6 q<0 \\
& \Rightarrow(\alpha-\beta)^2+(\beta-\gamma)^2+(\gamma-\alpha)^2<0
\end{aligned}
$$
A1
if all roots were real $(\alpha-\beta)^2+(\beta-\gamma)^2+(\gamma-\alpha)^2 \geq 0$
R1
Note: Condone strict inequality in the $R 1$ line.
Note: Do not award AOR1.
$\Rightarrow$ roots cannot all be real $\quad A G$
[2 marks]
d. $p^2=(-7)^2=49$ and $3 q=51$
A1
so $p^2<3 q \Rightarrow$ the equation has at least one complex root
$R 1$
Note: Allow equivalent comparisons; e.g. checking $p^2<6 q$
[2 marks]
e.i. use of GDC (eg graphs or tables)
(M1)
$q=12$
A1
[2 marks]
e.ii.complex roots appear in conjugate pairs (so if complex roots occur the other root will be real OR all 3 roots will be real).
OR
a cubic curve always crosses the $x$-axis at at least one point.
R1
[1 mark]
f.i. attempt to expand $(\alpha+\beta+\gamma+\delta)^2$
(M1)
$$
\begin{aligned}
& (\alpha+\beta+\gamma+\delta)^2=\alpha^2+\beta^2+\gamma^2+\delta^2+2(\alpha \beta+\alpha \gamma+\alpha \delta+\beta \gamma+\beta \delta+\gamma \delta) \\
& \Rightarrow \alpha^2+\beta^2+\gamma^2+\delta^2=(\alpha+\beta+\gamma+\delta)^2-2(\alpha \beta+\alpha \gamma+\alpha \delta+\beta \gamma+\beta \delta+\gamma \delta) \\
& \left(\Rightarrow \alpha^2+\beta^2+\gamma^2+\delta^2=\right) p^2-2 q \quad \text { A1 }
\end{aligned}
$$
A1
(A1)
[3 marks]
f.ii. $p^2<2 q$ OR $p^2-2 q<0$
A1
Note: Allow $F T$ on their result from part (f)(i).
[1 mark]
g. $4<6$ OR $2^2-2 \times 3<0 \quad$ R1
hence there is at least one complex root. $\boldsymbol{A G}$
Note: Allow $\boldsymbol{F T}$ from part (f)(ii) for the $\boldsymbol{R}$ mark provided numerical reasoning is seen.
[1 mark]
h.i. $\left(p^2>2 q\right)(81>2 \times 24)$ (so) nothing can be deduced
$R 1$
Note: Do not allow $\boldsymbol{F T}$ for the $\boldsymbol{R}$ mark.
[1 mark]
h.ii-1
A1
[1 mark]
h.iiiattempt to express as a product of a linear and cubic factor
M1
$(x+1)\left(x^3-10 x^2+34 x-12\right)$
A1A1
Note: Award $A 1$ for each factor. Award at most $A 1 A O$ if not written as a product.
since for the cubic, $p^2<3 q(100<102)$
$R 1$
there is at least one complex root
AG
[4 marks]
Question
This question asks you to explore the behaviour and key features of cubic polynomials of the form $x^3-3 c x+d$.
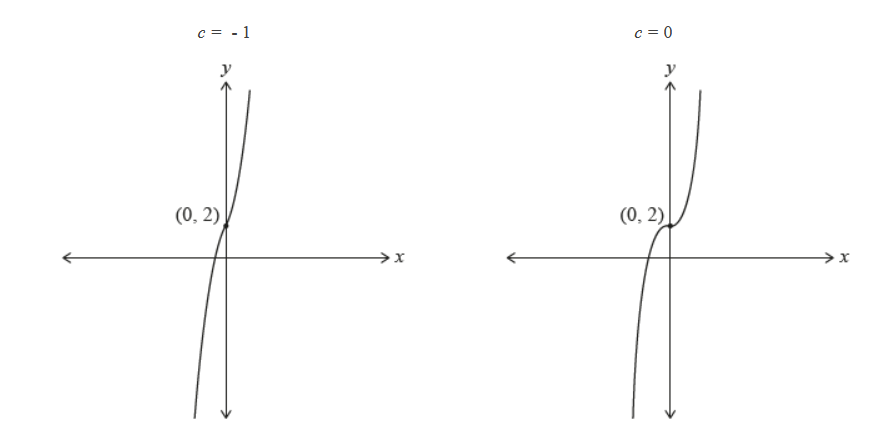
Consider the function $f(x)=x^3-3 c x+2$ for $x \in \mathbb{R}$ and where $c$ is a parameter, $c \in \mathbb{R}$.
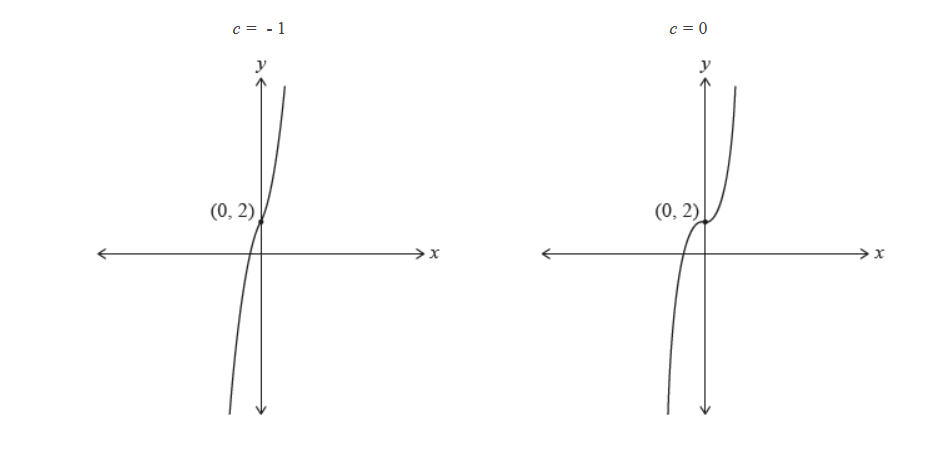
The graphs of $y=f(x)$ for $c=-1$ and $c=0$ are shown in the following diagrams.
On separate axes, sketch the graph of $y=f(x)$ showing the value of the $y$-intercept and the coordinates of any points with zero gradient, for
Hence, or otherwise, find the set of values of $c$ such that the graph of $y=f(x)$ has
Given that the graph of $y=f(x)$ has one local maximum point and one local minimum point, show that
Hence, for $c>0$, find the set of values of $c$ such that the graph of $y=f(x)$ has
a.i. $c=1$
[3]
a.ii $c=2$
[3]
b. Write down an expression for $f^{\prime}(x)$.
[1]
c.i. a point of inflexion with zero gradient.
c.ii.one local maximum point and one local minimum point.
[2]
c.iiino points where the gradient is equal to zero.
d.i. the $y$-coordinate of the local maximum point is $2 c_2^{\frac{3}{2}}+2$.
[1]
d.iithe $y$-coordinate of the local minimum point is $-2 c_2^{\frac{3}{2}}+2$.
[1]
[3]
e.i. exactly one $x$-axis intercept.
[1]
e.ii.exactly two $x$-axis intercepts.
[2]
e.iiexactly three $x$-axis intercepts.
$[2]$
f. Consider the function $g(x)=x^3-3 c x+d$ for $x \in \mathbb{R}$ and where $c, d \in \mathbb{R}$.
[2]
Find all conditions on $c$ and $d$ such that the graph of $y=g(x)$ has exactly one $x$-axis intercept, explaining your reasoning.
▶️Answer/Explanation
a.i.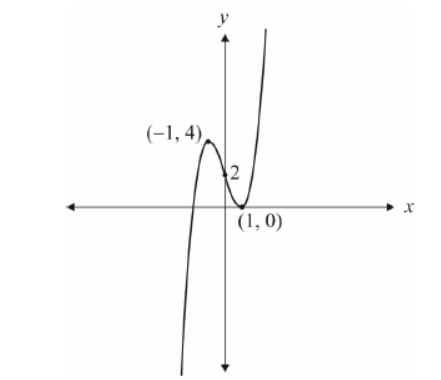
$c=1$ : positive cubic with correct $y$-intercept labelled $\quad$ A1
local maximum point correctly labelled
A1
local minimum point correctly labelled
A1
[3 marks]
a.ii.
$c=2$ : positive cubic with correct $y$-intercept labelled
A1
local maximum point correctly labelled
local minimum point correctly labelled
A1
A1
Note: Accept the following exact answers:
Local maximum point coordinates $(-\sqrt{2}, 2+4 \sqrt{2})$.
Local minimum point coordinates $(\sqrt{2}, 2-4 \sqrt{2})$.
[3 marks]
b. $f(x)=3 x^2-3 c$
A1
Note: Accept $3 x^2-3 c$ (an expression).
[1 mark]
c.i. $c=0$
A1
[1 mark]
c.ii.considers the number of solutions to their $f(x)=0$
(M1)
$$
\begin{aligned}
& 3 x^2-3 c=0 \\
& c>0 \quad \text { A1 }
\end{aligned}
$$
A1
[2 marks]
C.iiic $<0$
A1
Note: The (M1) in part (c)(ii) can be awarded for work shown in either (ii) or (iii).
[1 mark]
d.i. attempts to solve their $f(x)=0$ for $x$
(M1)
$$
x \pm \sqrt{c}
$$
Note: Award (A1) if either $x=-\sqrt{c}$ or $x=\sqrt{c}$ is subsequently considered. Award the above (M1)(A1) if this work is seen in part (c).
correctly evaluates $f(-\sqrt{c}) \quad$ A1
$$
f(-\sqrt{c})=-c^{\frac{3}{2}}+3 c^{\frac{3}{2}}+2(=-c \sqrt{c}+3 c \sqrt{c}+2)
$$
the $y$-coordinate of the local maximum point is $2 c^{\frac{3}{2}}+2 \quad \boldsymbol{A G}$
[3 marks]
d.ii.
correctly evaluates $f(\sqrt{c}) \quad$ A1
$$
f(\sqrt{c})=c_2^{\frac{3}{2}}-3 c^{\frac{3}{2}}+2(=c \sqrt{c}-3 c \sqrt{c}+2)
$$
the $y$-coordinate of the local minimum point is $-2 c_2^{\frac{3}{2}}+2 \quad \boldsymbol{A G}$
[1 mark]
e.i. the graph of $y=f(x)$ will have one $x$-axis intercept if
EITHER
$-2 c_2^{\frac{3}{2}}+2>0$ (or equivalent reasoning) $R 1$
OR
the minimum point is above the $x$-axis $R 1$
Note: Award $\boldsymbol{R} 1$ for a rigorous approach that does not (only) refer to sketched graphs.
THEN
$$
0<c<1
$$
A1
Note: Condone $c<1$. The $\boldsymbol{A} 1$ is independent of the $\boldsymbol{R}$.
e.iithe graph of $y=f(x)$ will have two $x$-axis intercepts if
EITHER
$-2 c^{\frac{3}{2}}+2=0$ (or equivalent reasoning)
(M1)
OR
evidence from the graph in part(a)(i) $\quad$ (M1)
THEN
$c=1 \quad$ A1
[2 marks]
e.iithe graph of $y=f(x)$ will have three $x$-axis intercepts if
EITHER
$-2 c_2^{\frac{3}{2}}+2<0$ (or equivalent reasoning)
(M1)
OR
reasoning from the results in both parts (e)(i) and (e)(ii)
(M1)
THEN
$c>1 \quad$ A1
[2 marks]
f. case 1:
$c \leq 0$ (independent of the value of $d$ )
A1
EITHER
$g^{\prime}(x)=0$ does not have two solutions (has no solutions or 1 solution)
R1
OR
$$
\Rightarrow g^{\prime}(x) \geq 0 \text { for } x \in^{\sim} \quad R 1
$$
OR
the graph of $y=f(x)$ has no local maximum or local minimum points, hence any vertical translation of this graph $(y=g(x))$ will also have no local maximum or local minimum points
R1
THEN
therefore there is only one $x$-axis intercept $\boldsymbol{A G}$
Note: Award at most AOR1 if only $c<0$ is considered.
case 2
$c>0$
$\left(-\sqrt{c}, 2 c_2^{\frac{3}{2}}+d\right)$ is a local maximum point and $\left(\sqrt{c},-2 c_2^{\frac{3}{2}}+d\right)$ is a local minimum point
(A1)
Note: Award (A1) for a correct $y$-coordinate seen for either the maximum or the minimum.
considers the positions of the local maximum point and/or the local minimum point
(M1)
EITHER
considers both points above the $x$-axis or both points below the $x$-axis
OR
considers either the local minimum point only above the $x$-axis OR the local maximum point only below the $x$-axis
THEN
$d>2 c_2^{\frac{3}{2}}$ (both points above the $x$-axis)
A1
$d<-2 c_2^{\frac{3}{2}}$ (both points above the $x$-axis)
A1
Note: Award at most (A1)(M1)AOAO for case 2 if $c>0$ is not clearly stated.
Question may 2022
This question asks you to explore properties of a family of curves of the type $y^2=x^3+a x+b$ for various values of $a$ and $b$, where $a, b \in$ N.
On the same set of axes, sketch the following curves for $-2 \leq x \leq 2$ and $-2 \leq y \leq 2$, clearly indicating any points of intersection with the coordinate axes.
Now, consider curves of the form $y^2=x^3+b$, for $x \geq-\sqrt[3]{b}$, where $b \in \mathbb{Z}^{+}$.
Next, consider the curve $y^2=x^3+x, x \geq 0$
The curve $y^2=x^3+x$ has two points of inflexion. Due to the symmetry of the curve these points have the same $x$-coordinate.
$\mathrm{P}(x, y)$ is defined to be a rational point on a curve if $x$ and $y$ are rational numbers.
The tangent to the curve $y^2=x^3+a x+b$ at a rational point $\mathrm{P}$ intersects the curve at another rational point $\mathrm{Q}$.
Let $C$ be the curve $y^2=x^3+2$, for $x \geq-\sqrt[3]{2}$. The rational point $\mathrm{P}(-1,-1)$ lies on $C$.
a.i. $y^2=x^3, x \geq 0$
a.ii $y^2=x^3+1, x \geq-1$
b.i. Write down the coordinates of the two points of inflexion on the curve $y^2=x^3+1$
b.ii.By considering each curve from part (a), identify two key features that would distinguish one curve from the other.
c. By varying the value of $b$, suggest two key features common to these curves.
d.i. Show that $\frac{\mathrm{d} y}{\mathrm{~d} x}= \pm \frac{3 x^2+1}{2 \sqrt{x^3+x}}$, for $x>0$
d.ii.Hence deduce that the curve $y^2=x^3+x$ has no local minimum or maximum points.
e. Find the value of this $x$-coordinate, giving your answer in the form $x=\sqrt{\frac{p \sqrt{3}+q}{r}}$, where $p, q, r \in \mathbb{Z}$.
f.i. Find the equation of the tangent to $C$ at $P$.
f.ii. Hence, find the coordinates of the rational point $\mathrm{Q}$ where this tangent intersects $C$, expressing each coordinate as a fraction.
g. The point $\mathrm{S}(-1,1)$ also lies on $C$. The line [QS] intersects $C$ at a further point. Determine the coordinates of this point.
▶️Answer/Explanation
Markscheme
a.i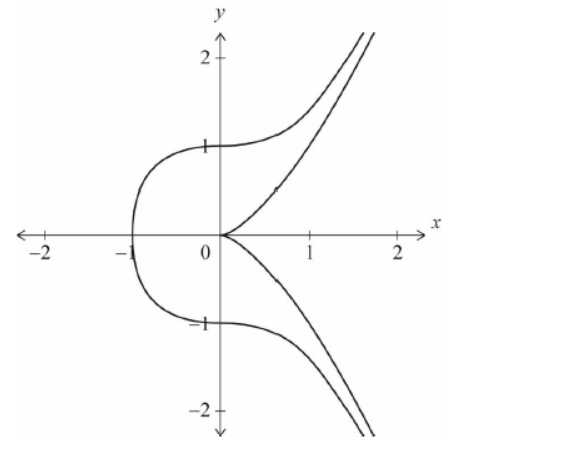
approximately symmetric about the $x$-axis graph of $y^2=x^3$
A1
including cusp/sharp point at $(0,0)$
A1
[2 marks]
Note: Final $\boldsymbol{A 1}$ can be awarded if intersections are in approximate correct place with respect to the axes shown. Award $\boldsymbol{A 1 A 1 A 1 A O}$ if graphs ‘merge’ or ‘cross’ or are discontinuous at $x$-axis but are otherwise correct. Award $A 1 A 0 A 0 A O$ if only one correct branch of both curves are seen.
Note: If they sketch graphs on separate axes, award a maximum of 2 marks for the ‘best’ response seen. This is likely to be A1A1AOAO.
a.iiapproximately symmetric about the $x$-axis graph of $y^2=x^3+1$ with approximately correct gradient at axes intercepts
A1
some indication of position of intersections at $x=-1, y= \pm 1$
A1
[2 marks]
Note: Final $\boldsymbol{A 1}$ can be awarded if intersections are in approximate correct place with respect to the axes shown. Award $\boldsymbol{A 1 A 1 A 1 A O}$ if graphs ‘merge’ or ‘cross’ or are discontinuous at $x$-axis but are otherwise correct. Award A1AOAOAO if only one correct branch of both curves are seen.
Note: If they sketch graphs on separate axes, award a maximum of 2 marks for the ‘best’ response seen. This is likely to be $\boldsymbol{A 1 A 1 A O A O}$.
b.i. $(0,1)$ and $(0,-1)$
A1
[1 mark]
b.iiAny two from:
$y^2=x^3$ has a cusp/sharp point, (the other does not)
graphs have different domains
$y^2=x^3+1$ has points of inflexion, (the other does not)
graphs have different $x$-axis intercepts (one goes through the origin, and the other does not)
graphs have different $y$-axis intercepts
A1
Note: Follow through from their sketch in part (a)(i). In accordance with marking rules, mark their first two responses and ignore any subsequent.
[1 mark]
c. Any two from:
as , $x \rightarrow \infty, y \rightarrow \pm \infty$
as $x \rightarrow \infty, y^2=x^3+b$ is approximated by $y^2=x^3$ (or similar)
they have $x$ intercepts at $x=-\sqrt[3]{b}$
they have $y$ intercepts at $y=( \pm) \sqrt{b}$
they all have the same range
$y=0$ (or $x$-axis) is a line of symmetry
they all have the same line of symmetry $(y=0)$
they have one $x$-axis intercept
they have two $y$-axis intercepts
they have two points of inflexion
at $x$-axis intercepts, curve is vertical/infinite gradient
there is no cusp/sharp point at $x$-axis intercepts $\boldsymbol{A 1 A 1}$
Note: The last example is the only valid answer for things “not” present. Do not credit an answer of “they are all symmetrical” without some reference to the line of symmetry.
Note: Do not allow same/ similar shape or equivalent.
Note: In accordance with marking rules, mark their first two responses and ignore any subsequent.
[2 marks],
d.i. METHOD 1
attempt to differentiate implicitly M1
$$
\begin{aligned}
& 2 y \frac{\mathrm{d} y}{\mathrm{~d} x}=3 x^2+1 \quad \text { A1 } \\
& \frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{3 x^2+1}{2 y} \text { OR }( \pm) 2 \sqrt{x^3+x} \frac{\mathrm{d} y}{\mathrm{~d} x}=3 x^2+1 \quad \text { A1 } \\
& \frac{\mathrm{d} y}{\mathrm{~d} x}= \pm \frac{3 x^2+1}{2 \sqrt{x^3+x}} \quad \text { AG }
\end{aligned}
$$
METHOD 2
attempt to use chain rule $y=( \pm) \sqrt{x^3+x} \quad$ M1
$$
\frac{\mathrm{d} y}{\mathrm{~d} x}=( \pm) \frac{1}{2}\left(x^3+x\right)^{-\frac{1}{2}}\left(3 x^2+1\right) \quad \text { A1A1 }
$$
Note: Award $\boldsymbol{A} \mathbf{1}$ for $( \pm) \frac{1}{2}\left(x^3+x\right)^{-\frac{1}{2}}, \boldsymbol{A} \boldsymbol{1}$ for $\left(3 x^2+1\right)$
$$
\frac{\mathrm{d} y}{\mathrm{~d} x}= \pm \frac{3 x^2+1}{2 \sqrt{x^3+x}} \quad \text { AG }
$$
[3 marks]
d.ii.EITHER
local minima/maxima occur when $\frac{d y}{d x}=0$
$1+3 x^2=0$ has no (real) solutions (or equivalent) $\quad \boldsymbol{R} \mathbf{r}$
OR
$$
\left(x^2 \geq 0 \Rightarrow\right) 3 x^2+1>0, \text { so } \frac{\mathrm{d} y}{\mathrm{~d} x} \neq 0 \quad \text { R1 }
$$
THEN
so, no local minima/maxima exist $\quad \boldsymbol{A G}$
[1 mark]
e. EITHER
attempt to use quotient rule to find $\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2} \quad M 1$
$$
\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}=( \pm) \frac{12 x \sqrt{x+x^3}-\left(1+3 x^2\right)\left(x+x^3\right)^{-\frac{1}{2}}\left(1+3 x^2\right)}{4\left(x+x^3\right)} \quad \text { A1A1 }
$$
Note: Award $\boldsymbol{A} 1$ for correct $12 x \sqrt{x+x^3}$ and correct denominator, $\boldsymbol{A} \boldsymbol{1}$ for correct $-\left(1+3 x^2\right)\left(x+x^3\right)^{-\frac{1}{2}}\left(1+3 x^2\right)$.
Note: Future $\boldsymbol{A}$ marks may be awarded if the denominator is missing or incorrect.
stating or using $\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}=0$ (may be seen anywhere)
(M1)
$$
12 x \sqrt{x+x^3}=\left(1+3 x^2\right)\left(x+x^3\right)^{-\frac{1}{2}}\left(1+3 x^2\right)
$$
OR
attempt to use product rule to find $\frac{\mathrm{d}^2 y}{d x^2} \quad \boldsymbol{M}$ I
$$
\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}=\frac{1}{2}\left(3 x^2+1\right)\left(-\frac{1}{2}\right)\left(3 x^2+1\right)\left(x^3+x\right)^{-\frac{3}{2}}+3 x\left(x^3+x\right)^{-\frac{1}{2}} \quad \text { A1A1 }
$$
Note: Award $\boldsymbol{A} 1$ for correct first term, $\boldsymbol{A} \mathbf{1}$ for correct second term.
setting $\frac{d^2 y}{d x^2}=0$
(M1)
OR
attempts implicit differentiation on $2 y \frac{\mathrm{d} y}{\mathrm{~d} x}=3 x^2+1 \quad$ M1
$2\left(\frac{\mathrm{d} y}{\mathrm{~d} x}\right)^2+2 y \frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}=6 x$
A1
recognizes that $\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}=0$
(M1)
$\frac{\mathrm{d} y}{\mathrm{~d} x}= \pm \sqrt{3 x}$
$( \pm) \frac{3 x^2+1}{2 \sqrt{x^3+x}}=( \pm) \sqrt{3 x}$
(A1)
THEN
$$
\begin{aligned}
& 12 x\left(x+x^3\right)=\left(1+3 x^2\right)^2 \\
& 12 x^2+12 x^4=9 x^4+6 x^2+1 \\
& 3 x^4+6 x^2-1=0
\end{aligned}
$$
A1
attempt to use quadratic formula or equivalent
(M1)
$x^2=\frac{-6 \pm \sqrt{48}}{6}$
$(x>0 \Rightarrow) x=\sqrt{\frac{2 \sqrt{3}-3}{3}}(p=2, q=-3, r=3) \quad$ A1
Note: Accept any integer multiple of $p, q$ and $r$ (e.g. 4, – 6 and 6).
[7 marks]
f.i. attempt to find tangent line through $(-1,-1)$
(M1)
$$
y+1=-\frac{3}{2}(x+1) \text { OR } y=-1.5 x-2.5 \quad \text { A1 }
$$
[2 marks]
f.ii. attempt to solve simultaneously with $y^2=x^3+2$
(M1)
Note: The $\boldsymbol{M} 1$ mark can be awarded for an unsupported correct answer in an incorrect format (e.g. (4. 25, – 8. 875)).
obtain $\left(\frac{17}{4},-\frac{71}{8}\right)$
A1
[2 marks]
g. attempt to find equation of [QS]
(M1)
$$
\frac{y-1}{x+1}=-\frac{79}{42}(=-1.88095 \ldots)
$$
(A1)
solve simultaneously with $y^2=x^3+2$
(M1)
$$
\begin{aligned}
& x=0.28798 \ldots\left(=\frac{127}{441}\right) \quad \text { A1 } \\
& y=-1.4226 \ldots\left(=\frac{13175}{9261}\right) \quad \text { A1 } \\
& (0.228,-1.42)
\end{aligned}
$$
OR
attempt to find vector equation of [QS]
(M1)
$$
\begin{aligned}
& \left(\begin{array}{l}
x \\
y
\end{array}\right)=\left(\begin{array}{c}
-1 \\
1
\end{array}\right)+\lambda\left(\begin{array}{c}
\frac{21}{4} \\
-\frac{79}{8}
\end{array}\right) \\
& x=-1+\frac{21}{4} \lambda \\
& y=1-\frac{79}{8} \lambda
\end{aligned}
$$
(A1)
attempt to solve $\left(1-\frac{79}{8} \lambda\right)^2=\left(-1+\frac{21}{4} \lambda\right)^3+2$
(M1)
$$
\lambda=0.2453 \ldots
$$
$x=0.28798 \ldots\left(=\frac{127}{441}\right) \quad$ A1
$y=-1.4226 \ldots\left(=\frac{13175}{9261}\right) \quad$ A1
$(0.228,-1.42)$
[5 marks]
Question mAy 2022
This question asks you to explore cubic polynomials of the form $(x-r)\left(x^2-2 a x+a^2+b^2\right)$ for $x \in \mathbb{R}$ and corresponding cubic equations with one real root and two complex roots of the form $(z-r)\left(z^2-2 a z+a^2+b^2\right)=0$ for $z \in \mathbb{C}$.
In parts (a), (b) and (c), let $r=1, a=4$ and $b=1$.
Consider the equation $(z-1)\left(z^2-8 z+17\right)=0$ for $z \in C$.
Consider the function $f(x)=(x-1)\left(x^2-8 x+17\right)$ for $x \in \mathbb{R}$
Consider the function $g(x)=(x-r)\left(x^2-2 a x+a^2+b^2\right)$ for $x \in \mathbb{R}$ where $r, a \in \mathbb{R}$ and $b \in \mathbb{R}, b>0$
The equation $(z-r)\left(z^2-2 a z+a^2+b^2\right)=0$ for $z \in \mathbb{C}$ has roots $r$ and $a \pm b$ where $r, a \in \mathbb{R}$ and $b \in \mathbb{R}, b>0$.
On the Cartesian plane, the points $\mathrm{C}_1\left(a, \sqrt{g^{\prime}(a)}\right)$ and $\mathrm{C}_2\left(a,-\sqrt{g^{\prime}(a)}\right)$ represent the real and imaginary parts of the complex roots of the equation $(z-r)\left(z^2-2 a z+a^2+b^2\right)=0$
The following diagram shows a particular curve of the form $y=(x-r)\left(x^2-2 a x+a^2+16\right)$ and the tangent to the curve at the point $\mathrm{A}(a, 80)$. The curve and the tangent both intersect the $x$-axis at the point $\mathrm{R}(-2,0)$. The points $\mathrm{C}_1$ and $\mathrm{C}_2$ are also shown.
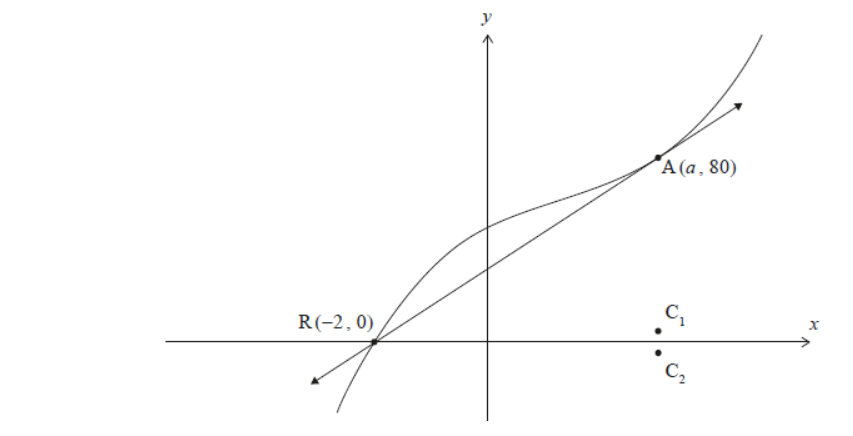
Consider the curve $y=(x-r)\left(x^2-2 a x+a^2+b^2\right)$ for $a \neq r, b>0$. The points $\mathrm{A}(a, g(a))$ and $\mathrm{R}(r, 0)$ are as defined in part (d)(ii). The curve has a point of inflexion at point $P$.
Consider the special case where $a=r$ and $b>0$.
a.i. Given that 1 and $4+\mathrm{i}$ are roots of the equation, write down the third root.
a.ii.Verify that the mean of the two complex roots is 4 .
[1]
b. Show that the line $y=x-1$ is tangent to the curve $y=f(x)$ at the point $\mathrm{A}(4,3)$.
[1]
c. Sketch the curve $y=f(x)$ and the tangent to the curve at point A, clearly showing where the tangent crosses the $x$-axis.
d.i. Show that $g^{\prime}(x)=2(x-r)(x-a)+x^2-2 a x+a^2+b^2$
[2]
d.ii.Hence, or otherwise, prove that the tangent to the curve $y=g(x)$ at the point $\mathrm{A}(a, g(a))$ intersects the $x$-axis at the point $\mathrm{R}(r, 0)$.
e. Deduce from part (d)(i) that the complex roots of the equation $(z-r)\left(z^2-2 a z+a^2+b^2\right)=0$ can be expressed as $a \pm \mathrm{i} \sqrt{g^{\prime}(a)}$.
$[6]$
f.i. Use this diagram to determine the roots of the corresponding equation of the form $(z-r)\left(z^2-2 a z+a^2+16\right)=0$ for $z \in \mathbb{C}$.
f.ii. State the coordinates of $\mathrm{C}_2$.
g.i. Show that the $x$-coordinate of $\mathrm{P}$ is $\frac{1}{3}(2 a+r)$.
[1]
You are not required to demonstrate a change in concavity.
g.ii.Hence describe numerically the horizontal position of point $\mathrm{P}$ relative to the horizontal positions of the points $\mathrm{R}$ and $\mathrm{A}$.
h.i. Sketch the curve $y=(x-r)\left(x^2-2 a x+a^2+b^2\right)$ for $a=r=1$ and $b=2$.
[2]
h.ii.For $a=r$ and $b>0$, state in terms of $r$, the coordinates of points $\mathrm{P}$ and $\mathrm{A}$.
[1]
▶️Answer/Explanation
Markscheme
a.i. 4 – i $A 1$
[1 mark]
a.iimean $=\frac{1}{2}(4+\mathrm{i}+4-\mathrm{i}) \quad \boldsymbol{A 1}$
$$
=4 \quad \boldsymbol{A G}
$$
[1 mark]
b. METHOD 1
attempts product rule differentiation
(M1)
Note: Award (M1) for attempting to express $f(x)$ as $f(x)=x^3-9 x^2+25 x-17$
$f(x)=(x-1)(2 x-8)+x^2-8 x+17\left(f(x)=3 x^2-18 x+25\right) \quad$ A1
$f(4)=1$
A1
Note: Where $f(x)$ is correct, award $\boldsymbol{A} 1$ for solving $f(x)=1$ and obtaining $x=4$.
EITHER
$y-3=1(x-4) \quad$ A1
OR
$$
\begin{aligned}
& y=x+c \\
& 3=4+c \Rightarrow c=-1
\end{aligned}
$$
A1
OR
states the gradient of $y=x-1$ is also 1 and verifies that $(4,3)$ lies on the line $y=x-1$
A1
THEN
so $y=x-1$ is the tangent to the curve at $\mathrm{A}(4,3) \quad \boldsymbol{A G}$
Note: Award a maximum of (MO)AOA1A1 to a candidate who does not attempt to find $f(x)$.
METHOD 2
sets $f(x)=x-1$ to form $x-1=(x-1)\left(x^2-8 x+17\right)$
(M1)
EITHER
$(x-1)\left(x^2-8 x+16\right)=0\left(x^3-9 x^2+24 x-16=0\right) \quad$ A1
attempts to solve a correct cubic equation
(M1)
$$
(x-1)(x-4)^2=0 \Rightarrow x=1,4
$$
OR
recognises that $x \neq 1$ and forms $x^2-8 x+17=1\left(x^2-8 x+16=0\right) \quad$ A1 attempts to solve a correct quadratic equation
(M1)
$$
(x-4)^2=0 \Rightarrow x=4
$$
THEN
$x=4$ is a double root $\quad R 1$
so $y=x-1$ is the tangent to the curve at $\mathrm{A}(4,3) \quad \boldsymbol{A G}$
Note: Candidates using this method are not required to verify that $y=3$.
[4 marks]
c.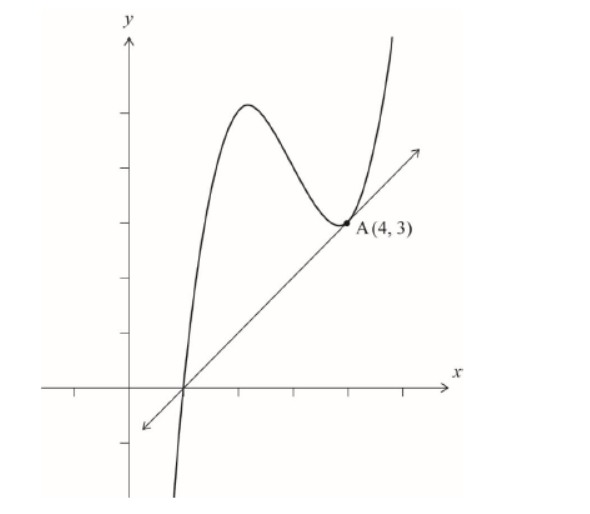
a positive cubic with an $x$-intercept $(x=1)$, and a local maximum and local minimum in the first quadrant both positioned to the left of A
A1
Note: As the local minimum and point A are very close to each other, condone graphs that seem to show these points coinciding. For the point of tangency, accept labels such as $\mathrm{A},(4,3)$ or the point labelled from both axes. Coordinates are not required.
a correct sketch of the tangent passing through A and crossing the $x$-axis at the same point $(x=1)$ as the curve
A1
Note: Award $\boldsymbol{A 1 A O}$ if both graphs cross the $x$-axis at distinctly different points.
[2 marks]
d.i.EITHER
$$
g^{\prime}(x)=(x-r)(2 x-2 a)+x^2-2 a x+a^2+b^2
$$
(M1)A1
OR
$$
g(x)=x^3-(2 a+r) x^2+\left(a^2+b^2+2 a r\right) x-\left(a^2+b^2\right) r
$$
attempts to find $g^{\prime}(x) \quad$ M1
$$
\begin{aligned}
& g^{\prime}(x)=3 x^2-2(2 a+r) x+a^2+b^2+2 a r \\
& =2 x^2-2(a+r) x+2 a r+x^2-2 a x+a^2+b^2 \\
& \left(=2\left(x^2-a x-r x+a r\right)+x^2-2 a x+a^2+b^2\right)
\end{aligned}
$$
A1
THEN
$$
g^{\prime}(x)=2(x-r)(x-a)+x^2-2 a x+a^2+b^2 \quad \text { AG }
$$
[2 marks]
d.iiMETHOD 1
$$
\begin{aligned}
& g(a)=b^2(a-r) \\
& g^{\prime}(a)=b^2
\end{aligned}
$$
(A1)
attempts to substitute their $g(a)$ and $g^{\prime}(a)$ into $y-g(a)=g^{\prime}(a)(x-a) \quad$ M1
$$
y-b^2(a-r)=b^2(x-a)
$$
EITHER
$$
\begin{aligned}
& y=b^2(x-r)\left(y=b^2 x-b^2 r\right) \quad \text { A1 } \\
& \text { sets } y=0 \text { so } b^2(x-r)=0 \quad \text { M1 } \\
& b>0 \Rightarrow x=r \text { OR } b \neq 0 \Rightarrow x=r \quad \text { R1 }
\end{aligned}
$$
OR
$$
\begin{array}{ll}
\text { sets } y=0 \text { so }-b^2(a-r)=b^2(x-a) & \text { M1 } \\
b>0 \text { OR } b \neq 0 \Rightarrow-(a-r)=x-a & \text { R1 } \\
x=r \quad \text { A1 } &
\end{array}
$$
THEN
so the tangent intersects the $x$-axis at the point $\mathrm{R}(r, 0) \quad \boldsymbol{A G}$
METHOD 2
$$
\begin{aligned}
& g^{\prime}(a)=b^2 \\
& g(a)=b^2(a-r)
\end{aligned}
$$
(A1)
attempts to substitute their $g(a)$ and $g^{\prime}(a)$ into $y=g^{\prime}(a) x+c$ and attempts to find $c \quad$ M1
$$
c=-b^2 r
$$
EITHER
$$
\begin{aligned}
& y=b^2(x-r)\left(y=b^2 x-b^2 r\right) \quad \text { A1 } \\
& \text { sets } y=0 \text { so } b^2(x-r)=0 \quad \text { M1 } \\
& b>0 \Rightarrow x=r \text { OR } b \neq 0 \Rightarrow x=r \quad \text { R1 }
\end{aligned}
$$
OR
$$
\begin{aligned}
& \text { sets } y=0 \text { so } b^2(x-r)=0 \quad \text { M1 } \\
& b>0 \text { OR } b \neq 0 \Rightarrow x-r=0 \quad \text { R1 } \\
& x=r \quad \text { A1 }
\end{aligned}
$$
METHOD 3
$$
g^{\prime}(a)=b^2
$$
(A1)
the line through $R(r, 0)$ parallel to the tangent at $\mathrm{A}$ has equation
$$
y=b^2(x-r)
$$
A1
sets $g(x)=b^2(x-r)$ to form $b^2(x-r)=(x-r)\left(x^2-2 a x+a^2+b^2\right) \quad$ M1
$$
\begin{aligned}
& b^2=x^2-2 a x+a^2+b^2,(x \neq r) \\
& (x-a)^2=0 \quad \text { A1 }
\end{aligned}
$$
A1
A1
since there is a double root $(x=a)$, this parallel line through $R(r, 0)$ is the required tangent at A $\quad \boldsymbol{R} 1$
[6 marks]
e. EITHER
$g^{\prime}(a)=b^2 \Rightarrow b=\sqrt{g^{\prime}(a)}($ since $b>0) \quad$ R1
Note: Accept $b= \pm \sqrt{g^{\prime}(a)}$.
OR
$(a \pm b \mathrm{i}=) a \pm \mathrm{i} \sqrt{b^2}$ and $g^{\prime}(a)=b^2 \quad$ R1
THEN
hence the complex roots can be expressed as $a \pm \mathrm{i} \sqrt{g^{\prime}(a)} \quad \boldsymbol{A G}$
[1 mark]
f.i. $b=4$ (seen anywhere)
A1
EITHER
attempts to find the gradient of the tangent in terms of $a$ and equates to 16
(M1)
OR
substitutes $r=-2, x=a$ and $y=80$ to form $80=(a-(-2))\left(a^2-2 a^2+a^2+16\right)$
(M1)
OR
substitutes $r=-2, x=a$ and $y=80$ into $y=16(x-r)$
(M1)
THEN
$\frac{80}{a+2}=16 \Rightarrow a=3$
roots are -2 (seen anywhere) and $3 \pm 4 \mathrm{i}$
A1A1
Note: Award $\boldsymbol{A} \boldsymbol{1}$ for -2 and $\boldsymbol{A} \boldsymbol{1}$ for $3 \pm 4$ i. Do not accept coordinates.
[4 marks]
f.ii. $(3,-4)$
A1
Note: Accept ” $x=3$ and $y=-4$ “.
Do not award $\boldsymbol{A 1 F T}$ for $(a,-4)$.
[1 mark]
g.i. $g^{\prime}(x)=2(x-r)(x-a)+x^2-2 a x+a^2+b^2$
attempts to find $g$ ” $(x) \quad M 1$
$g^{\prime \prime}(x)=2(x-a)+2(x-r)+2 x-2 a(=6 x-2 r-4 a)$
sets $g^{\prime \prime}(x)=0$ and correctly solves for $x$
A1
for example, obtaining $x-r+2(x-a)=0$ leading to $3 x=2 a+r$
So $x=\frac{1}{3}(2 a+r) \quad$ AG
Note: Do not award $\boldsymbol{A 1}$ if the answer does not lead to the $\boldsymbol{A G}$.
[2 marks]
g.iipoint $\mathrm{P}$ is $\frac{2}{3}$ of the horizontal distance (way) from point $\mathrm{R}$ to point $\mathrm{A}$
A1
Note: Accept equivalent numerical statements or a clearly labelled diagram displaying the numerical relationship. Award $\boldsymbol{A O}$ for non-numerical statements such as ” $\mathrm{P}$ is between $\mathrm{R}$ and $\mathrm{A}$, closer to $\mathrm{A}$ “.
[1 mark]
h.i. $y=(x-1)\left(x^2-2 x+5\right)$
(A1)
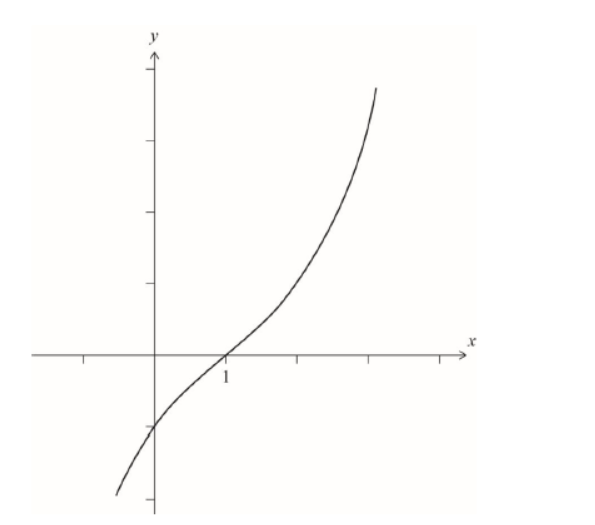
a positive cubic with no stationary points and a non-stationary point of inflexion at $x=1$
A1
Note: Graphs may appear approximately linear. Award this $\boldsymbol{A} 1$ if a change of concavity either side of $x=1$ is apparent. Coordinates are not required and the $y$-intercept need not be indicated.
[2 marks]
h.ii. $(r, 0) \quad A 1$
[1 mark]
Question may 2021
This question asks you to explore the behaviour and some key features of the function $f_n(x)=x^n(a-x)^n$, where $a \in \mathbb{R}^{+}$and $n \in Z^{+}$.
In parts (a) and (b), only consider the case where $a=2$.
Consider $f_1(x)=x(2-x)$
Consider $f_n(x)=x^n(2-x)^n$, where $n \in \mathrm{Z}^{+}, n>1$
Now consider $f_n(x)=x^n(a-x)^n$ where $a \in \mathbb{R}^{+}$and $n \in \mathrm{Z}^{+}, n>1$
By using the result from part (f) and considering the sign of $f_n^{\prime}(-1)$, show that the point $(0,0)$ on the graph of $y=f_n(x)$ is
a. Sketch the graph of $y=f_1(x)$, stating the values of any axes intercepts and the coordinates of any local maximum or minimum points.
[3]
b. Use your graphic display calculator to explore the graph of $y=f_n(x)$ for
[6]
– the odd values $n=3$ and $n=5$;
– the even values $n=2$ and $n=4$.
Hence, copy and complete the following table.

c. Show that $f_n^{\prime}(x)=n x^{n-1}(a-2 x)(a-x)^{n-1}$.
d. State the three solutions to the equation $f_n^{\prime}(x)=0$.
e. Show that the point $\left(\frac{a}{2}, f_n\left(\frac{a}{2}\right)\right)$ on the graph of $y=f_n(x)$ is always above the horizontal axis.
f. Hence, or otherwise, show that $f_n^{\prime}\left(\frac{a}{4}\right)>0$, for $n \in Z^{+}$.
[2]
g.i.a local minimum point for even values of $n$, where $n>1$ and $a \in \mathbb{R}^{+}$.
g.iia point of inflexion with zero gradient for odd values of $n$, where $n>1$ and $a \in \mathbb{R}^{+}$.
[2]
h. Consider the graph of $y=x^n(a-x)^n-k$, where $n \in \mathbb{Z}^{+}, a \in \mathbb{R}^{+}$and $k \in \mathbb{R}$.
State the conditions on $n$ and $k$ such that the equation $x^n(a-x)^n=k$ has four solutions for $x$.
▶️Answer/Explanation
Markscheme
a.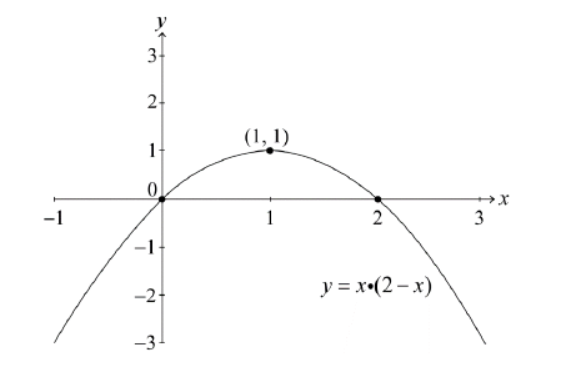
inverted parabola extended below the $x$-axis
A1
$x$-axis intercept values $x=0,2 \quad \boldsymbol{A 1}$
Note: Accept a graph passing through the origin as an indication of $x=0$.
local maximum at $(1,1)$
A1
Note: Coordinates must be stated to gain the final $\boldsymbol{A 1}$.
Do not accept decimal approximations.
[3 marks]
b.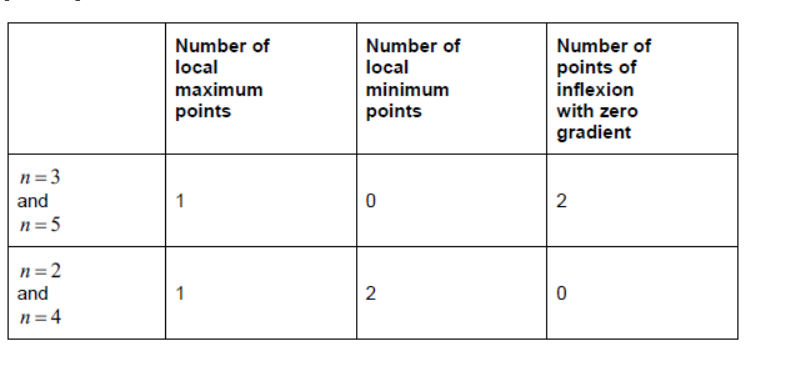
Note: Award $\boldsymbol{A} \boldsymbol{1}$ for each correct value.
For a table not sufficiently or clearly labelled, assume that their values are in the same order as the table in the question paper and award marks accordingly.
[6 marks]
c. METHOD 1
attempts to use the product rule
$f_n^{\prime}(x)=-n x^n(a-x)^{n-1}+n x^{n-1}(a-x)^n$
(M1)
$A 141$
Note: Award $\boldsymbol{A} 1$ for a correct $u \frac{\mathrm{d} v}{\mathrm{~d} x}$ and $\boldsymbol{A} 1$ for a correct $v \frac{\mathrm{d} u}{\mathrm{~d} x}$.
EITHER
attempts to factorise $f_n^{\prime}(x)$ (involving at least one of $n x^{n-1}$ or $\left.(a-x)^{n-1}\right)$
(M1)
$=n x^{n-1}(a-x)^{n-1}((a-x)-x)$
A1
OR
(M1)
$=(-x)\left(n x^{n-1}\right)(a-x)^{n-1}+(a-x)\left(n x^{n-1}\right)(a-x)^{n-1}$
A1
THEN
$f_n^{\prime}(x)=n x^{n-1}(a-2 x)(a-x)^{n-1} \quad$ AG
Note: Award the final (M1)A1 for obtaining any of the following forms:
$$
\begin{aligned}
f_n^{\prime}(x)=n x^n(a-x)^n\left(\frac{a-x-x}{x(a-x)}\right) ; \quad f_n^{\prime}(x)=\frac{n x^n(a-x)^n}{x(a-x)}(a-x-x) \\
f_n^{\prime}(x)=n x^{n-1}\left((a-x)^n-x(a-x)^{n-1}\right) \\
f_n^{\prime}(x)=(a-x)^{n-1}\left(n x^{n-1}(a-x)^n-n x^n\right)
\end{aligned}
$$
METHOD 2
$$
\begin{aligned}
& f_n(x)=(x(a-x))^n \quad \text { (M1) } \\
& =\left(a x-x^2\right)^n \quad \text { A1 }
\end{aligned}
$$
(M1)
attempts to use the chain rule
(M1)
$f_n^{\prime}(x)=n(a-2 x)\left(a x-x^2\right)^{n-1}$
A1A1
Note: Award $\boldsymbol{A} \mathbf{1}$ for $n(a-2 x)$ and $\boldsymbol{A}$ for $\left(a x-x^2\right)^{n-1}$.
$$
f_n^{\prime}(x)=n x^{n-1}(a-2 x)(a-x)^{n-1} \quad \text { AG }
$$
[5 marks]
d. $x=0, x=\frac{a}{2}, x=a$
A2
Note: Award $\boldsymbol{A} \boldsymbol{1}$ for either two correct solutions or for obtaining $\boldsymbol{x}=\mathbf{0}, \boldsymbol{x}=-\boldsymbol{a}, \boldsymbol{x}=-\frac{a}{2}$ Award $\boldsymbol{A O}$ otherwise.
[2 marks]
e.
attempts to find an expression for $f_n\left(\frac{a}{2}\right)$ (MI)
$$
\begin{aligned}
& f_n\left(\frac{a}{2}\right)=\left(\frac{a}{2}\right)^n\left(a-\frac{a}{2}\right)^n \\
& =\left(\frac{a}{2}\right)^n\left(\frac{a}{2}\right)^n\left(=\left(\frac{a}{2}\right)^{2 n}\right),\left(=\left(\left(\frac{a}{2}\right)^n\right)^2\right) \quad \boldsymbol{A 1}
\end{aligned}
$$
EITHER
since $a \in \mathbb{R}^{+},\left(\frac{a}{2}\right)^{2 n}>0$ (for $n \in \mathbb{Z}^{+}, n>1$ and so $f_n\left(\frac{a}{2}\right)>0$ ) $\quad \boldsymbol{R 1}$
Note: Accept any logically equivalent conditions/statements on $a$ and $n$.
Award $\boldsymbol{R O}$ if any conditions/statements specified involving $a, n$ or both are incorrect.
OR
(since $\left.a \in \mathbb{R}^{+}\right), \frac{a}{2}$ raised to an even power $(2 n)$ (or equivalent reasoning) is always positive (and so $\left.f_n\left(\frac{a}{2}\right)>0\right) \quad R 1$
Note: The condition $a \in \mathbb{R}^{+}$is given in the question. Hence some candidates will assume $a \in \mathbb{R}^{+}$and not state it. In these instances, award $R 1$ for a convincing argument.
Accept any logically equivalent conditions/statements on on $a$ and $n$.
Award $R O$ if any conditions/statements specified involving $a, n$ or both are incorrect.
THEN
so $\left(\frac{a}{2}, f_n\left(\frac{a}{2}\right)\right)$ is always above the horizontal axis $\quad \boldsymbol{A G}$
Note: Do not award (M1)AOR1.
[3 marks]
f. METHOD 1
$$
f_n^{\prime}\left(\frac{a}{4}\right)=n\left(\frac{a}{4}\right)^{n-1}\left(a-\frac{a}{2}\right)\left(a-\frac{a}{4}\right)^{n-1}\left(=n\left(\frac{a}{4}\right)^{n-1}\left(\frac{a}{2}\right)\left(\frac{3 a}{4}\right)^{n-1}\right) \quad \text { A1 }
$$
EITHER
$$
n\left(\frac{a}{4}\right)^{n-1}\left(\frac{a}{2}\right)\left(\frac{3 a}{4}\right)^{n-1}>0 \text { as } a \in \mathbb{R}^{+} \text {and } n \in \mathbb{Z}^{+} \quad \text { R1 }
$$
OR
$$
n\left(\frac{a}{4}\right)^{n-1},\left(a-\frac{a}{2}\right) \text { and }\left(a-\frac{a}{4}\right)^{n-1} \text { are all }>0 \quad \text { R1 }
$$
Note: Do not award AOR1.
Accept equivalent reasoning on correct alternative expressions for $f_n^{\prime}\left(\frac{a}{4}\right)$ and accept any logically equivalent conditions/statements on $a$ and $n$. Exceptions to the above are condone $n>1$ and condone $n>0$.
An alternative form for $f_n^{\prime}\left(\frac{a}{4}\right)$ is $(2 n)(3)^{n-1}\left(\frac{a}{4}\right)^{2 n-1}$
THEN
hence $f_n{ }^{\prime}\left(\frac{a}{4}\right)>0 \quad \quad \boldsymbol{A G}$
METHOD 2
$f_n(0)=0$ and $f_n\left(\frac{a}{2}\right)>0 \quad$ A1
(since $f_n$ is continuous and there are no stationary points between $x=0$ and $x=\frac{a}{2}$ )
the gradient (of the curve) must be positive between $x=0$ and $x=\frac{a}{2} \quad \boldsymbol{R}$
Note: Do not award $\boldsymbol{A O R 1}$.
hence $f_n{ }^{\prime}\left(\frac{a}{4}\right)>0 \quad \quad A G$
[2 marks]
g.i. $f_n^{\prime}(-1)=n(-1)^{n-1}(a+2)(a+1)^{n-1}$
for $n$ even:
$n(-1)^{n-1}(=-n)<0 \quad$ and $(a+2),(a+1)^{n-1}$ are both $\left.>0\right) \quad$ R1
$f_n^{\prime}(-1)<0 \quad \boldsymbol{A 1}$
$f_n^{\prime}(0)=0$ and $f_n{ }^{\prime}\left(\frac{a}{4}\right)>0$ (seen anywhere) $\quad \boldsymbol{A 1}$
Note: Candidates can give arguments based on the sign of $(-1)^{n-1}$ to obtain the $\boldsymbol{R}$ mark.
For example, award $R 1$ for the following:
If $n$ is even, then $n-1$ is odd and hence $(-1)^{n-1}<0(=-1)$.
Do not award ROA1.
The second $\boldsymbol{A} 1$ is independent of the other two marks.
The $\boldsymbol{A}$ marks can be awarded for correct descriptions expressed in words.
Candidates can state $(0,0)$ as a point of zero gradient from part (d) or show, state or explain (words or diagram) that $f_n{ }^{\prime}(0)=0$. The last $\boldsymbol{A}$ mark can be awarded for a clearly labelled diagram showing changes in the sign of the gradient.
The last $\boldsymbol{A} \boldsymbol{1}$ can be awarded for use of a specific case (e.g. $n=2$ ).
hence $(0,0)$ is a local minimum point $\boldsymbol{A G}$
[3 marks]
g.iifor $n$ odd:
$n(-1)^{n-1}(=n)<0$, (and $(a+2),(a+1)^{n-1}$ are both $\left.>0\right)$ so $f_n^{\prime}(-1)>0 \quad$ R1
Note: Candidates can give arguments based on the sign of $(-1)^{n-1}$ to obtain the $\boldsymbol{R}$ mark. For example, award $R 1$ for the following:
If $n$ is odd, then $n-1$ is even and hence $(-1)^{n-1}>0(=1)$.
$f_n{ }^{\prime}(0)=0$ and $f_n{ }^{\prime}\left(\frac{a}{4}\right)>0$ (seen anywhere) $\quad \boldsymbol{A 1}$
Note: The $A 1$ is independent of the $R 1$.
Candidates can state $(0,0)$ as a point of zero gradient from part (d) or show, state or explain (words or diagram) that $f_n$ ‘ $(0)=0$. The last $\boldsymbol{A}$ mark can be awarded for a clearly labelled diagram showing changes in the sign of the gradient.
The last $\boldsymbol{A} 1$ can be awarded for use of a specific case (e.g. $n=3$ ).
hence $(0,0)$ is a point of inflexion with zero gradient
AG
[2 marks]
h. considers the parity of $n$
(M1)
Note: Award $\boldsymbol{M 1}$ for stating at least one specific even value of $n$.
$n$ must be even (for four solutions)
A1
Note: The above 2 marks are independent of the 3 marks below.
$0<k<\left(\frac{a}{2}\right)^{2 n}$
A1A1A1
Note: Award $\boldsymbol{A} \boldsymbol{1}$ for the correct lower endpoint, $\boldsymbol{A} \boldsymbol{1}$ for the correct upper endpoint and $\boldsymbol{A} \boldsymbol{1}$ for strict inequality signs.
The third $\boldsymbol{A 1}$ (strict inequality signs) can only be awarded if $\boldsymbol{A 1 A 1}$ has been awarded.
For example, award $\boldsymbol{A 1 A 1 A O}$ for $0 \leq k \leq\left(\frac{a}{2}\right)^{2 n}$. Award $\boldsymbol{A 1 A O A O}$ for $k>0$.
Award $\mathbf{A 1 A O A O}$ for $0<k<f_n\left(\frac{a}{2}\right)$.
[5 marks]
Question
This question asks you to explore the behaviour and key features of cubic polynomials of the form $x^3-3 c x+d$.
Consider the function $f(x)=x^3-3 c x+2$ for $x \in \mathbb{R}$ and where $c$ is a parameter, $c \in \mathbb{R}$. The graphs of $y=f(x)$ for $c=-1$ and $c=0$ are shown in the following diagrams.
On separate axes, sketch the graph of $y=f(x)$ showing the value of the $y$-intercept and the coordinates of any points with zero gradient, for
Hence, or otherwise, find the set of values of $c$ such that the graph of $y=f(x)$ has
Given that the graph of $y=f(x)$ has one local maximum point and one local minimum point, show that
Hence, for $c>0$, find the set of values of $c$ such that the graph of $y=f(x)$ has
a.i. $c=1$.
[3]
a.ii $c=2$.
$[3]$
b. Write down an expression for $f(x)$.
[1]
c.i. a point of inflexion with zero gradient.
[1]
c.ii.one local maximum point and one local minimum point.
[2]
c.iiino points where the gradient is equal to zero.
d.i. the $y$-coordinate of the local maximum point is $2 c^{\frac{3}{2}}+2$.
[3]
d.iithe $y$-coordinate of the local minimum point is $-2 c^{\frac{3}{2}}+2$.
[1]
e.i. exactly one $x$-axis intercept.
[2]
e.ii.exactly two $x$-axis intercepts.
[2]
e.iiiexactly three $x$-axis intercepts.
[2]
f. Consider the function $g(x)=x^3-3 c x+d$ for $x \in \mathbb{R}$ and where $c, d \in \mathbb{R}$.
Find all conditions on $c$ and $d$ such that the graph of $y=g(x)$ has exactly one $x$-axis intercept, explaining your reasoning.
▶️Answer/Explanation
Markscheme
a.i.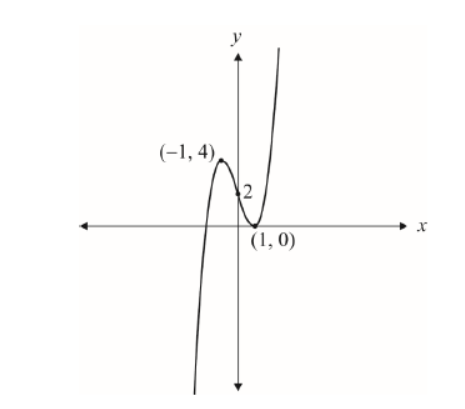
$c=1:$ positive cubic with correct $y$-intercept labelled $\quad \boldsymbol{A 1}$
local maximum point correctly labelled $\quad$ A1
local minimum point correctly labelled A1
[3 marks]
a.ii 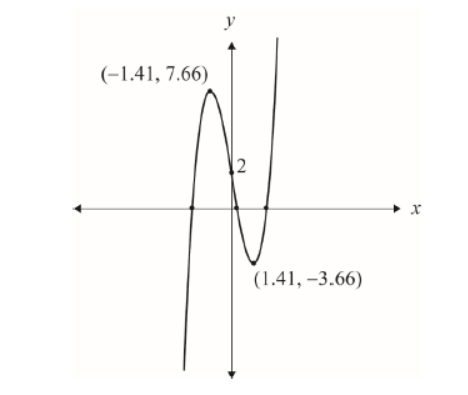
$c=2$ : positive cubic with correct $y$-intercept labelled
A1
local maximum point correctly labelled
local minimum point correctly labelled
A1
A1
Note: Accept the following exact answers:
Local maximum point coordinates $(-\sqrt{2}, 2+4 \sqrt{2})$.
Local minimum point coordinates $(\sqrt{2}, 2-4 \sqrt{2})$.
[3 marks]
b. $f(x)=3 x^2-3 c$
A1
Note: Accept $3 x^2-3 c$ (an expression).
[1 mark]
C.i. $c=0$
A1
[1 mark]
c.ii.considers the number of solutions to their $f(x)=0$
(M1)
$$
\begin{aligned}
& 3 x^2-3 c=0 \\
& c>0 \quad \text { A1 }
\end{aligned}
$$
A1
[2 marks]
c. iiic $<0$
A1
Note: The (M1) in part (c)(ii) can be awarded for work shown in either (ii) or (iii).
[1 mark]
d.i.attempts to solve their $f(x)=0$ for $x$
(M1)
$x \pm \sqrt{c}$
(A1)
Note: Award (A1) if either $x=-\sqrt{c}$ or $x=\sqrt{c}$ is subsequently considered.
Award the above (M1)(A1) if this work is seen in part (c).
correctly evaluates $f(-\sqrt{c}) \quad$ A1
$f(-\sqrt{c})=-c_2^{\frac{3}{2}}+3 c^{\frac{3}{2}}+2(=-c \sqrt{c}+3 c \sqrt{c}+2)$
the $y$-coordinate of the local maximum point is $2 c^{\frac{3}{2}}+2 \quad \boldsymbol{A G}$
[3 marks]
d.ii.
correctly evaluates $f(\sqrt{c}) \quad$ A1
$f(\sqrt{c})=c^{\frac{3}{2}}-3 c^{\frac{3}{2}}+2(=c \sqrt{c}-3 c \sqrt{c}+2)$
the $y$-coordinate of the local minimum point is $-2 c_2^{\frac{3}{2}}+2 \quad \boldsymbol{A G}$
[1 mark]
e.i. the graph of $y=f(x)$ will have one $x$-axis intercept if
EITHER
$-2 c^{\frac{3}{2}}+2>0$ (or equivalent reasoning) $R 1$
OR
the minimum point is above the $x$-axis $R 1$
Note: Award $\boldsymbol{R} 1$ for a rigorous approach that does not (only) refer to sketched graphs.
THEN
$0<c<1$
A1
Note: Condone $c<1$. The $\boldsymbol{A} \boldsymbol{1}$ is independent of the $\boldsymbol{R} 1$.
e.iithe graph of $y=f(x)$ will have two $x$-axis intercepts if EITHER
$-2 c^{\frac{3}{2}}+2=0$ (or equivalent reasoning)
(M1)
OR
evidence from the graph in part(a)(i)
(M1)
THEN
$c=1$
A1
[2 marks]
e.iithe graph of $y=f(x)$ will have three $x$-axis intercepts if
EITHER
$-2 c_2^{\frac{3}{2}}+2<0$ (or equivalent reasoning)
(M1)
OR
reasoning from the results in both parts (e)(i) and (e)(ii)
(M1)
THEN
$c>1 \quad$ A1
[2 marks]
f. case 1:
$c \leq 0$ (independent of the value of $d$ )
A1
EITHER
$g^{\prime}(x)=0$ does not have two solutions (has no solutions or 1 solution)
R1
OR
$$
\Rightarrow g^{\prime}(x) \geq 0 \text { for } x \in^{\sim} \quad \text { R1 }
$$
OR
the graph of $y=f(x)$ has no local maximum or local minimum points, hence any vertical translation of this graph $(y=g(x))$ will also have no local maximum or local minimum points
$R 1$
THEN
therefore there is only one $x$-axis intercept
AG
Note: Award at most AOR1 if only $c<0$ is considered.
case 2
$c>0$
$\left(-\sqrt{c}, 2 c_2^{\frac{3}{2}}+d\right)$ is a local maximum point and $\left(\sqrt{c},-2 c_2^{\frac{3}{2}}+d\right)$ is a local minimum point
(A1)
Note: Award (A1) for a correct $y$-coordinate seen for either the maximum or the minimum.
considers the positions of the local maximum point and/or the local minimum point
(M1)
EITHER
considers both points above the $x$-axis or both points below the $x$-axis
OR
considers either the local minimum point only above the $x$-axis OR the local maximum point only below the $x$-axis
THEN
$d>2 c^{\frac{3}{2}}$ (both points above the $x$-axis) $\quad \boldsymbol{A 1}$
$d<-2 c_2^3$ (both points above the $x$-axis) $\quad \boldsymbol{A 1}$
Note: Award at most (A1)(M1)AOAO for case 2 if $c>0$ is not clearly stated.
Question nov 2020
a.i. Write down the remainder when $14^{2022}$ is divided by 7 .
a.ii.Use Fermat’s little theorem to find the remainder when $14^{2022}$ is divided by 17.
b.i.Prove that a number in base 13 is divisible by 6 if, and only if, the sum of its digits is divisible by 6 .
b.ii.The base 13 number $1 y 93 y 25$ is divisible by 6 . Find the possible values of the digit $y$.
▶️Answer/Explanation
Markscheme
a.i. the remainder is 0
A1
[1 mark]
a.ii.14 ${ }^{16} \equiv 1(\bmod 17)$ (from Fermat’s little theorem)
(A1)
$$
14^{2022}=14^{16 \times 126+6}
$$
(M1)
Note: Award $\boldsymbol{M} 1$ for a RHS exponent consistent with the correct use of Fermat’s little theorem.
$$
14^{2022} \equiv 14^6(\bmod 17)(\equiv 15(\bmod 17)) \quad \boldsymbol{A 1}
$$
the remainder is $15 \quad A 1$
[4 marks]
b.i. METHOD 1
let $N=a_n 13^n+a_{n-1} 13^{n-1}+\ldots+a_1 13+a_0 \quad \boldsymbol{M 1}$
Note: The above $\boldsymbol{M} \boldsymbol{1}$ is independent of the $\boldsymbol{A}$ marks below.
$$
13 \equiv 1(\bmod 6) \quad \boldsymbol{A 1}
$$
EITHER
$13^x \equiv 1(\bmod 6)$ (for all $\left.x \in \mathbb{N}\right) \quad \boldsymbol{A 1}$
OR
$$
N \equiv a_n 1^n+a_{n-1} 1^{n-1}+\ldots+a_1 1+a_0(\bmod 6)\left(N \equiv a_n+a_{n-1}+\ldots+a_1+a_0(\bmod 6)\right) \quad \boldsymbol{A 1}
$$
THEN
so $N \equiv 0(\bmod 6)$ if and only if $a_n+a_{n-1}+\ldots+a_1+a_0 \equiv 0(\bmod 6) \quad R 1$
so $6 N$ if and only if $6\left(a_n+a_{n-1}+\ldots+a_1+a_0\right) \quad \boldsymbol{A G}$
METHOD 2
let $N=a_n 13^n+a_{n-1} 13^{n-1}+\ldots+a_1 13+a_0$
(M1)
$N=\left(a_n+a_{n-1}+\ldots+a_1+a_0\right)+(13-1)\left(a_n\left(13^{n-1}+\ldots+13^0\right)+a_{n-1}\left(13^{n-2}+\ldots+13^0\right)+\ldots+a_1 13^0\right) \quad$ M1A1
Note: Award $\boldsymbol{M} 1$ for attempting to express $N$ in the form $N=\left(a_n+a_{n-1}+\ldots+a_1+a_0\right)+(13-1) M$.
as $6(13-1) M \quad R 1$
so $6 N$ if and only if $6\left(a_n+a_{n-1}+\ldots+a_1+a_0\right) \quad \boldsymbol{A G}$
[4 marks]
b.iiMETHOD 1
the sum of the digits is $2 y+20$
(A1)
uses $2 y+20=6 k$ (or equivalent) to attempt to find a valid value of $y$
(M1)
$y=2,5,8,11(B) \quad$ A1A1
Note: Award $\boldsymbol{A 1}$ for $y=2,5,8$ and $\boldsymbol{A} 1$ for $y=11(B)$.
METHOD 2
$$
\begin{aligned}
& (1 y 93 y 25)_{13}=1 \times 13^6+y \times 13^5+9 \times 13^4+3 \times 13^3+y \times 13^2+2 \times 13^1+5 \times 13^0 \\
& =371462 y+5090480
\end{aligned}
$$
attempts to find a valid value of $y$ such that
$$
\begin{aligned}
& 371462 y+5090480 \equiv 0(\bmod 6) \\
& y=2,5,8,11(B) \quad \text { A1A1 }
\end{aligned}
$$
(M1)
Note: Award $\boldsymbol{A 1}$ for $y=2,5,8$ and $\boldsymbol{A} 1$ for $y=11(B)$.
[4 marks]
Question 2022
This question asks you to investigate conditions for the existence of complex roots of polynomial equations of degree 3 and 4.
The cubic equation $x^3+p x^2+q x+r=0$, where $p, q, r \in \mathbb{R}$, has roots $\alpha, \beta$ and $\gamma$.
Consider the equation $x^3-7 x^2+q x+1=0$, where $q \in \mathbb{R}$.
Noah believes that if $p^2 \geq 3 q$ then $\alpha, \beta$ and $\gamma$ are all real.
Now consider polynomial equations of degree 4.
The equation $x^4+p x^3+q x^2+r x+s=0$, where $p, q, r, s \in \mathbb{R}$, has roots $\alpha, \beta, \gamma$ and $\delta$.
In a similar way to the cubic equation, it can be shown that:
$$
\begin{aligned}
& p=-(\alpha+\beta+\gamma+\delta) \\
& q=\alpha \beta+\alpha \gamma+\alpha \delta+\beta \gamma+\beta \delta+\gamma \delta \\
& r=-(\alpha \beta \gamma+\alpha \beta \delta+\alpha \gamma \delta+\beta \gamma \delta) \\
& s=\alpha \beta \gamma \delta .
\end{aligned}
$$
The equation $x^4-9 x^3+24 x^2+22 x-12=0$, has one integer root.
a. By expanding $(x-\alpha)(x-\beta)(x-\gamma)$ show that:
[3]
$$
\begin{aligned}
& p=-(\alpha+\beta+\gamma) \\
& q=\alpha \beta+\beta \gamma+\gamma \alpha \\
& r=-\alpha \beta \gamma .
\end{aligned}
$$
b.i. Show that $p^2-2 q=\alpha^2+\beta^2+\gamma^2$.
b.ii.Hence show that $(\alpha-\beta)^2+(\beta-\gamma)^2+(\gamma-\alpha)^2=2 p^2-6 q$.
c. Given that $p^2<3 q$, deduce that $\alpha, \beta$ and $\gamma$ cannot all be real.
d. Using the result from part (c), show that when $q=17$, this equation has at least one complex root.
e.i. By varying the value of $q$ in the equation $x^3-7 x^2+q x+1=0$, determine the smallest positive integer value of $q$ required to show that Noah is incorrect.
e.ii.Explain why the equation will have at least one real root for all values of $q$.
f.i. Find an expression for $\alpha^2+\beta^2+\gamma^2+\delta^2$ in terms of $p$ and $q$.
f.ii. Hence state a condition in terms of $p$ and $q$ that would imply $x^4+p x^3+q x^2+r x+s=0$ has at least one complex root.
g. Use your result from part (f)(ii) to show that the equation $x^4-2 x^3+3 x^2-4 x+5=0$ has at least one complex root.
[1]
h.i. State what the result in part (f)(ii) tells us when considering this equation $x^4-9 x^3+24 x^2+22 x-12=0$.
h.ii.Write down the integer root of this equation.
[1]
h.iiiBy writing $x^4-9 x^3+24 x^2+22 x-12$ as a product of one linear and one cubic factor, prove that the equation has at least one complex root.
$[4]$
▶️Answer/Explanation
Markscheme
a. attempt to expand $(x-\alpha)(x-\beta)(x-\gamma)$
$$
\begin{aligned}
& =\left(x^2-(\alpha+\beta) x+\alpha \beta\right)(x-\gamma) \text { OR }=(x-\alpha)\left(x^2-(\beta+\gamma) x+\beta \gamma\right) \\
& \left(x^3+p x^2+q x+r\right)=x^3-(\alpha+\beta+\gamma) x^2+(\alpha \beta+\beta \gamma+\gamma \alpha) x-\alpha \beta \gamma \quad \text { A1 }
\end{aligned}
$$
comparing coefficients:
$$
\begin{aligned}
& p=-(\alpha+\beta+\gamma) \quad \text { AG } \\
& q=(\alpha \beta+\beta \gamma+\gamma \alpha) \quad \text { AG } \\
& r=-\alpha \beta \gamma \quad \boldsymbol{A G}
\end{aligned}
$$
Note: For candidates who do not include the $\boldsymbol{A G}$ lines award full marks.
[3 marks]
b.i. $p^2-2 q=(\alpha+\beta+\gamma)^2-2(\alpha \beta+\beta \gamma+\gamma \alpha)$
(A1)
attempt to expand $(\alpha+\beta+\gamma)^2$
(M1)
$$
\begin{aligned}
& =\alpha^2+\beta^2+\gamma^2+2(\alpha \beta+\beta \gamma+\gamma \alpha)-2(\alpha \beta+\beta \gamma+\gamma \alpha) \text { or equivalent } \\
& =\alpha^2+\beta^2+\gamma^2 \quad \text { AG }
\end{aligned}
$$
$\boldsymbol{A G}$
Note: Accept equivalent working from RHS to LHS.
[3 marks]
b.ii.EITHER
$$
\begin{aligned}
& \text { attempt to expand }(\alpha-\beta)^2+(\beta-\gamma)^2+(\gamma-\alpha)^2 \quad \text { (M1) } \\
& =\left(\alpha^2+\beta^2-2 \alpha \beta\right)+\left(\beta^2+\gamma^2-2 \beta \gamma\right)+\left(\gamma^2+\alpha^2-2 \gamma \alpha\right) \quad \text { A1 } \\
& =2\left(\alpha^2+\beta^2+\gamma^2\right)-2(\alpha \beta+\beta \gamma+\gamma \alpha) \\
& =2\left(p^2-2 q\right)-2 q \text { or equivalent } \quad \text { A1 } \\
& =2 p^2-6 q \quad \text { AG }
\end{aligned}
$$
(M1)
$A 1$
A1
A1
OR
attempt to write $2 p^2-6 q$ in terms of $\alpha, \beta, \gamma$
(M1)
$$
\begin{aligned}
& =2\left(p^2-2 q\right)-2 q \\
& =2\left(\alpha^2+\beta^2+\gamma^2\right)-2(\alpha \beta+\beta \gamma+\gamma \alpha) \quad \text { A1 } \\
& =\left(\alpha^2+\beta^2-2 \alpha \beta\right)+\left(\beta^2+\gamma^2-2 \beta \gamma\right)+\left(\gamma^2+\alpha^2-2 \gamma \alpha\right) \\
& =(\alpha-\beta)^2+(\beta-\gamma)^2+(\gamma-\alpha)^2 \quad \text { AG }
\end{aligned}
$$
A1
Note: Accept equivalent working where LHS and RHS are expanded to identical expressions.
[3 marks]
c. $p^2<3 q \Rightarrow 2 p^2-6 q<0$
$\Rightarrow(\alpha-\beta)^2+(\beta-\gamma)^2+(\gamma-\alpha)^2<0$
A1
if all roots were real $(\alpha-\beta)^2+(\beta-\gamma)^2+(\gamma-\alpha)^2 \geq 0$
R1
Note: Condone strict inequality in the $R 1$ line.
Note: Do not award AOR1.
$\Rightarrow$ roots cannot all be real
$A G$
[2 marks]
d. $p^2=(-7)^2=49$ and $3 q=51$
A1
so $p^2<3 q \Rightarrow$ the equation has at least one complex root
R1
Note: Allow equivalent comparisons; e.g. checking $p^2<6 q$
[2 marks]
e.i.use of GDC (eg graphs or tables)
(M1)
$q=12 \quad \boldsymbol{A} 1$
[2 marks]
e.ii.complex roots appear in conjugate pairs (so if complex roots occur the other root will be real OR all 3 roots will be real).
OR
a cubic curve always crosses the $x$-axis at at least one point.
R1
[1 mark]
f.i. attempt to expand $(\alpha+\beta+\gamma+\delta)^2$
(M1)
$$
\begin{aligned}
& (\alpha+\beta+\gamma+\delta)^2=\alpha^2+\beta^2+\gamma^2+\delta^2+2(\alpha \beta+\alpha \gamma+\alpha \delta+\beta \gamma+\beta \delta+\gamma \delta) \\
& \Rightarrow \alpha^2+\beta^2+\gamma^2+\delta^2=(\alpha+\beta+\gamma+\delta)^2-2(\alpha \beta+\alpha \gamma+\alpha \delta+\beta \gamma+\beta \delta+\gamma \delta) \\
& \left(\Rightarrow \alpha^2+\beta^2+\gamma^2+\delta^2=\right) p^2-2 q \quad \text { A1 }
\end{aligned}
$$
A1
(A1)
[3 marks]
f.ii. $p^2<2 q$ OR $p^2-2 q<0$
A1
Note: Allow $F T$ on their result from part (f)(i).
[1 mark]
g. $4<6$ OR $2^2-2 \times 3<0 \quad$ R1
hence there is at least one complex root. $\quad \boldsymbol{A G}$
Note: Allow $\boldsymbol{F T}$ from part (f)(ii) for the $\boldsymbol{R}$ mark provided numerical reasoning is seen.
[1 mark]
h.i. $\left(p^2>2 q\right)(81>2 \times 24)$ (so) nothing can be deduced
R1
Note: Do not allow $\boldsymbol{F T}$ for the $\boldsymbol{R}$ mark.
[1 mark]
h.ii- 1
A1
[1 mark]
h.iiiattempt to express as a product of a linear and cubic factor
M1
$(x+1)\left(x^3-10 x^2+34 x-12\right)$
A1A1
Note: Award $\boldsymbol{A} \boldsymbol{1}$ for each factor. Award at most $\boldsymbol{A 1 A O}$ if not written as a product.
since for the cubic, $p^2<3 q(100<102)$
R1
there is at least one complex root
AG
[4 marks]
Question
A polynomial \(p(x)\) with real coefficients is of degree five. The equation \(p(x) = 0\) has a complex root 2 + i. The graph of \(y = p(x)\) has the x-axis as a tangent at (2, 0) and intersects the coordinate axes at (−1, 0) and (0, 4).
Find \(p(x)\) in factorised form with real coefficients.
▶️Answer/Explanation
Markscheme
other root is 2 – i (A1)
a quadratic factor is therefore \((x – 2 + i)(x – 2 – i)\) (M1)
\( = {x^2} – 4x + 5\) A1
x + 1 is a factor A1
\({(x – 2)^2}\) is a factor A1
\(p(x) = a(x + 1){(x – 2)^2}({x^2} – 4x + 5)\) (M1)
\(p(0) = 4 \Rightarrow a = \frac{1}{5}\) A1
\(p(x) = \frac{1}{5}(x + 1){(x – 2)^2}({x^2} – 4x + 5)\)
[7 marks]
Examiners report
Whilst most candidates knew that another root was \(2 – {\text{i}}\) , much fewer were able to find the quadratic factor. Surprisingly few candidates knew that \(\left( {x – 2} \right)\) must be a repeated factor and less surprisingly many did not recognise that the whole expression needed to be multiplied by \(\frac{1}{5}\).
Question
When \({x^2} + 4x – b\) is divided by \(x – a\) the remainder is 2.
Given that \(a,{\text{ }}b \in \mathbb{R}\), find the smallest possible value for \(b\).
▶️Answer/Explanation
Markscheme
\({a^2} + 4a – b = 2\) M1A1
EITHER
\({a^2} + 4a – (b + 2) = 0\)
as \(a\) is real \( \Rightarrow 16 + 4(b + 2) \geqslant 0\) M1A1
OR
\(b = {a^2} + 4a – 2\) M1
\( = {(a + 2)^2} – 6\) (A1)
THEN
\(b \geqslant – 6\)
hence smallest possible value for \(b\) is \( – 6\) A1
[5 marks]
Examiners report
For quite a difficult question, there were many good solutions for this, including many different methods. It was disturbing to see how many students did not seem to be aware of the remainder theorem, instead choosing to divide the polynomial.
Question
The polynomial \({x^4} + p{x^3} + q{x^2} + rx + 6\) is exactly divisible by each of \(\left( {x – 1} \right)\), \(\left( {x – 2} \right)\) and \(\left( {x – 3} \right)\).
Find the values of \(p\), \(q\) and \(r\).
▶️Answer/Explanation
Markscheme
METHOD 1
substitute each of \(x\) = 1,2 and 3 into the quartic and equate to zero (M1)
\(p + q + r = – 7\)
\(4p + 2q + r = – 11\) or equivalent (A2)
\(9p + 3q + r = – 29\)
Note: Award A2 for all three equations correct, A1 for two correct.
attempting to solve the system of equations (M1)
\(p\) = −7, \(q\) = 17, \(r\) = −17 A1
Note: Only award M1 when some numerical values are found when solving algebraically or using GDC.
METHOD 2
attempt to find fourth factor (M1)
\(\left( {x – 1} \right)\) A1
attempt to expand \({\left( {x – 1} \right)^2}\left( {x – 2} \right)\left( {x – 3} \right)\) M1
\({x^4} – 7{x^3} + 17{x^2} – 17x + 6\) (\(p\) = −7, \(q\) = 17, \(r\) = −17) A2
Note: Award A2 for all three values correct, A1 for two correct.
Note: Accept long / synthetic division.
[5 marks]
