Question
The function $f$ is defined by $f(x)=\frac{3 x+2}{4 x^2-1}$, for $x \in \mathbb{R}, x \neq p, x \neq q$.
The graph of $y=f(x)$ has exactly one point of inflexion.
The function $g$ is defined by $g(x)=\frac{4 x^2-1}{3 x+2}$, for $x \in \mathbb{R}, x \neq-\frac{2}{3}$.
a. Find the value of $p$ and the value of $q$.
[2]
b. Find an expression for $f(x)$.
[3]
c. Find the $x$-coordinate of the point of inflexion.
[2]
d. Sketch the graph of $y=f(x)$ for $-3 \leq x \leq 3$, showing the values of any axes intercepts, the coordinates of any local maxima and local minima, and giving the equations of any asymptotes.
e. Find the equations of all the asymptotes on the graph of $y=g(x)$.
$[4]$
f. By considering the graph of $y=g(x)-f(x)$, or otherwise, solve $f(x)<g(x)$ for $x \in \mathbb{R}$.
$[4]$
The graph of $y=f(x)$ has exactly one point of inflexion.
The function $g$ is defined by $g(x)=\frac{4 x^2-1}{3 x+2}$, for $x \in \mathbb{R}, x \neq-\frac{2}{3}$.
a. Find the value of $p$ and the value of $q$.
[2]
b. Find an expression for $f(x)$.
[3]
c. Find the $x$-coordinate of the point of inflexion.
[2]
d. Sketch the graph of $y=f(x)$ for $-3 \leq x \leq 3$, showing the values of any axes intercepts, the coordinates of any local maxima and local minima, and giving the equations of any asymptotes.
e. Find the equations of all the asymptotes on the graph of $y=g(x)$.
$[4]$
f. By considering the graph of $y=g(x)-f(x)$, or otherwise, solve $f(x)<g(x)$ for $x \in \mathbb{R}$.
$[4]$
▶️Answer/Explanation
Markscheme
a. attempt to solve $4 x^2-1=0$ e.g. by factorising $4 x^2-1$
(M1)
$p=\frac{1}{2}, q=-\frac{1}{2}$ or vice versa
A1
[2 marks]
b. attempt to use quotient rule or product rule
(M1)
EITHER
$f(x)=\frac{3\left(4 x^2-1\right)-8 x(3 x+2)}{\left(4 x^2-1\right)^2}\left(=\frac{-12 x^2-16 x-3}{\left(4 x^2-1\right)^2}\right) \quad$ A1A1
Note: Award $\boldsymbol{A} \mathbf{1}$ for each term in the numerator with correct signs, provided correct denominator is seen.
OR
$f(x)=-8 x(3 x+2)\left(4 x^2-1\right)^{-2}+3\left(4 x^2-1\right)^{-1} \quad \operatorname{A1A1}$
Note: Award $\boldsymbol{A 1}$ for each term.
c. attempt to find the local min point on $y=f(x)$ OR solve $f^{\prime \prime}(x)=0$
(M1)
$$
x=-1.60 \quad \text { A1 }
$$
[2 marks]
(M1)
$$
x=-1.60 \quad \text { A1 }
$$
[2 marks]
d.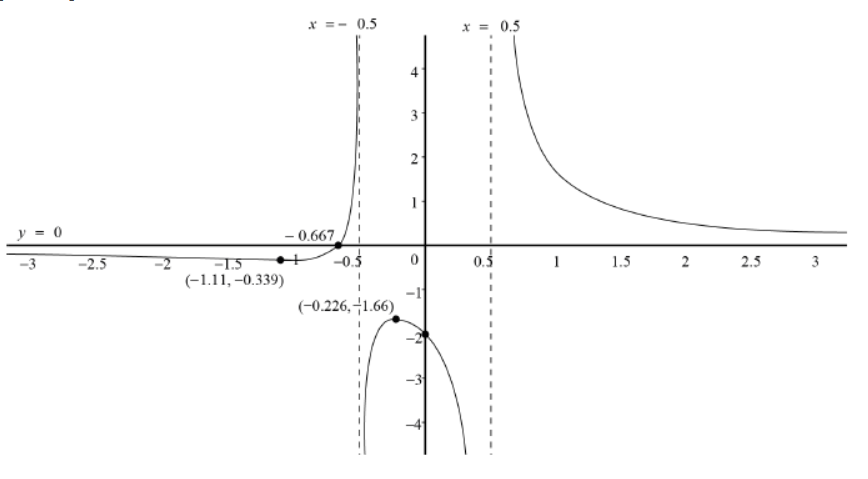

Note: Award $\boldsymbol{A} 1$ for both vertical asymptotes with their equations, award $\boldsymbol{A} \boldsymbol{1}$ for horizontal asymptote with equation, award $\boldsymbol{A} \mathbf{1}$ for each correct branch including asymptotic behaviour, coordinates of minimum and maximum points (may be seen next to the graph) and values of axes intercepts. If vertical asymptotes are absent (or not vertical) and the branches overlap as a consequence, award maximum AOA1AOA1A1.
[5 marks]
e. $x=-\frac{2}{3}(=-0.667) \quad A 1$
(oblique asymptote has) gradient $\frac{4}{3}(=1.33) \quad$ (A1)
appropriate method to find complete equation of oblique asymptote M1
$$
\begin{aligned}
& \frac{4}{3} x-\frac{8}{9} \\
& -\frac{8}{3} x-\frac{16}{\frac{9}{7}} \\
& y=\frac{4}{3} x-\frac{8}{9}(=1.33 x-0.889) \quad \text { A1 } \\
&
\end{aligned}
$$
Note: Do not award the final $\boldsymbol{A} 1$ if the answer is not given as an equation.
[4 marks]
[5 marks]
e. $x=-\frac{2}{3}(=-0.667) \quad A 1$
(oblique asymptote has) gradient $\frac{4}{3}(=1.33) \quad$ (A1)
appropriate method to find complete equation of oblique asymptote M1
$$
\begin{aligned}
& \frac{4}{3} x-\frac{8}{9} \\
& -\frac{8}{3} x-\frac{16}{\frac{9}{7}} \\
& y=\frac{4}{3} x-\frac{8}{9}(=1.33 x-0.889) \quad \text { A1 } \\
&
\end{aligned}
$$
Note: Do not award the final $\boldsymbol{A} 1$ if the answer is not given as an equation.
[4 marks]
f. attempting to find at least one critical value $(x=-0.568729 \ldots, x=1.31872 \ldots)$
(M1)
$-\frac{2}{3}<x<-0.569$ OR $-0.5<x<0.5$ OR $x>1.32$ A1A1A1
Note: Only penalize once for use of $\leq$ rather than $<$.
[4 marks]
(M1)
$-\frac{2}{3}<x<-0.569$ OR $-0.5<x<0.5$ OR $x>1.32$ A1A1A1
Note: Only penalize once for use of $\leq$ rather than $<$.
[4 marks]