Question
This question asks you to examine various polygons for which the numerical value of the area is the same as the numerical value of the perimeter. For example, a 3 by 6 rectangle has an area of 18 and a perimeter of 18.
For each polygon in this question, let the numerical value of its area be $A$ and let the numerical value of its perimeter be $P$.
An $n$-sided regular polygon can be divided into $n$ congruent isosceles triangles. Let $x$ be the length of each of the two equal sides of one such isosceles triangle and let $y$ be the length of the third side. The included angle between the two equal sides has magnitude $\frac{2 \pi}{n}$.
Part of such an $n$-sided regular polygon is shown in the following diagram.
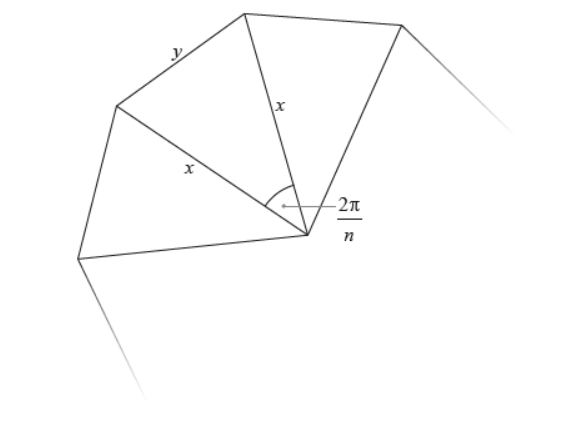
Consider a $n$-sided regular polygon such that $A=P$.
The Maclaurin series for $\tan x$ is $x+\frac{x^3}{3}+\frac{2 x^5}{15}+\ldots$
Consider a right-angled triangle with side lengths $a, b$ and $\sqrt{a^2+b^2}$, where $a \geq b$, such that $A=P$.
a. Find the side length, $s$, where $s>0$, of a square such that $A=P$.
b. Write down, in terms of $x$ and $n$, an expression for the area, $A_T$, of one of these isosceles triangles.
[1]
c. Show that $y=2 x \sin \frac{\pi}{n}$.
d. Use the results from parts (b) and (c) to show that $A=P=4 n \tan \frac{\pi}{n}$.
e.i.
$\lim _{n \rightarrow \infty}\left(4 n \tan \frac{\pi}{n}\right)$
e.ii.Interpret your answer to part (e)(i) geometrically.
f. Show that $a=\frac{8}{b-4}+4$.
g.i. By using the result of part (f) or otherwise, determine the three side lengths of the only two right-angled triangles for which $a, b, A, P \in \mathbb{Z}$.
[3]
g.ii.Determine the area and perimeter of these two right-angled triangles.
[1]
▶️Answer/Explanation
Markscheme
a. $A=s^2$ and $P=4 s$
(A1)
$$
\begin{aligned}
& A=P \Rightarrow s^2=4 s \\
& s(s-4)=0 \\
& \Rightarrow s=4(s>0)
\end{aligned}
$$
(M1)
Note: Award A1M1AO if both $s=4$ and $s=0$ are stated as final answers.
[3 marks]
b. $A_T=\frac{1}{2} x^2 \sin \frac{2 \pi}{n}$
A1
Note: Award $\boldsymbol{A} 1$ for a correct alternative form expressed in terms of $x$ and $n$ only.
[1 mark]
C. METHOD 1
$$
\text { uses } \sin \theta=\frac{\text { opp }}{\text { hyp }}
$$
(M1)
$$
\begin{aligned}
& \frac{y}{x}=\sin _{\frac{\pi}{n}} \frac{\pi}{A 1} \\
& y=2 x \sin \frac{\pi}{n} \quad \text { AG }
\end{aligned}
$$
METHOD 2
uses Pythagoras’ theorem $\left(\frac{y}{2}\right)^2+h^2=x^2$ and $h=x \cos \frac{\pi}{n}$
(M1)
$$
\begin{aligned}
& \left(\frac{y}{2}\right)^2+\left(x \cos ^{\frac{\pi}{n}}\right)^2=x^2\left(y^2=4 x^2\left(1-\cos ^2 \frac{\pi}{n}\right)\right) \\
& =4 x^2 \sin ^2 \frac{\pi}{n} \quad \boldsymbol{A} 1 \\
& y=2 x \sin _{\frac{\pi}{n}} \quad \boldsymbol{A G}
\end{aligned}
$$
METHOD 3
uses the cosine rule
(M1)
$$
\begin{aligned}
& y^2=2 x^2-2 x^2 \cos \frac{2 \pi}{n}\left(=2 x^2\left(1-\cos \frac{2 \pi}{n}\right)\right) \\
& =4 x^2 \sin ^2 \frac{\pi}{n} \quad \boldsymbol{A 1} \\
& y=2 x \sin \frac{\pi}{n} \quad \text { AG }
\end{aligned}
$$
METHOD 4
uses the sine rule
(M1)
$$
\begin{aligned}
& \frac{y}{\sin \frac{2 \pi}{n}}=\frac{x}{\sin \left(\frac{\pi}{2}-\frac{\pi}{n}\right)} \\
& y \cos _n^{-}=2 x \sin \frac{\pi}{n} \cos \frac{\pi}{n} \\
& y=2 x \sin _{\frac{\pi}{n}}^{\frac{\pi}{n}} \quad \text { AG }
\end{aligned}
$$
A1
[2 marks]
d. $A=P \Rightarrow n A_T=n y$
(M1)
Note: Award $\boldsymbol{M} 1$ for equating correct expressions for $A$ and $P$.
$\frac{1}{2} n x^2 \sin \frac{2 \pi}{n}=2 n x \sin _n^{-}\left(n x^2 \sin _n^{\frac{\pi}{-} \cos _n^{-}}=2 n x \sin _n^{\frac{\pi}{n}}\right)$
$\frac{1}{2} x^2 \sin \frac{2 \pi}{n}=2 x \sin _n^{-}\left(x^2 \sin _n^{-\frac{\pi}{n}} \cos _n^{-}=2 x \sin _n^{\frac{\pi}{n}}\right) \quad \boldsymbol{A 1}$
uses $\sin \frac{2 \pi}{n}=2 \sin _n^{\frac{\pi}{-} \cos _n^{-}}$(seen anywhere in part (d) or in part (b))
(M1)
$x^2 \sin _n^{\frac{\pi}{n}} \frac{\cos _n^{-}}{n}=2 x \sin _n^{-}$
attempts to either factorise or divide their expression
(M1)
$$
\begin{aligned}
& x \sin _n^{\frac{\pi}{n}}\left(x \cos _n^{-}-2\right)=0 \\
& x=\frac{2}{\cos _{\frac{\pi}{n}}^{\frac{\pi}{n}}},\left(x \sin \frac{\pi}{n} \neq 0\right) \text { (or equivalent) } \boldsymbol{A} \boldsymbol{1}
\end{aligned}
$$
EITHER
substitutes $x=\frac{2}{\cos _{\frac{\pi}{n}}^n}$ (or equivalent) into $P=n y$
(M1)
$P=2 n\left(\frac{2}{\cos _{\frac{\pi}{n}}^n}\right)\left(\sin _n^{\frac{\pi}{n}}\right) \quad \boldsymbol{A 1}$
Note: Other approaches are possible. For example, award $\boldsymbol{A} 1$ for $P=2 n x \cos _n^{\pi-\tan _n^{-}} \frac{\pi}{n}$ and $\boldsymbol{M} \boldsymbol{1}$ for substituting $x=\frac{2}{\cos ^\pi-\frac{\pi}{n}}$ into $P$.
OR
substitutes $x=\frac{2}{\cos _{\frac{\pi}{n}}^\pi}$ (or equivalent) into $A=n A_T$
(M1)
$$
A=\frac{1}{2} n\left(\frac{2}{\cos \frac{\pi}{n}}\right)^2\left(\sin \frac{2 \pi}{n}\right)
$$
THEN
$$
A=P=4 n \tan \frac{\pi}{n} \quad \quad A G
$$
[7 marks]
e.i. attempts to use the Maclaurin series for $\tan x$ with $x=\frac{\pi}{n}$
(M1)
$$
\begin{aligned}
& \tan _n^{\frac{\pi}{n}}=\frac{\pi}{n}+\frac{\left(\frac{\pi}{n}\right)^3}{3}+\frac{2\left(\frac{\pi}{n}\right)^5}{15}(+\ldots) \\
& 4 n \tan \frac{\pi}{n}=4 n\left(\frac{\pi}{n}+\frac{\pi^3}{3 n^3}+\frac{2 \pi^5}{15 n^5}(+\ldots)\right) \text { (or equivalent) } \\
& =4\left(\pi+\frac{\pi^3}{3 n^2}+\frac{2 \pi^5}{15 n^4}+\ldots\right) \\
& \Rightarrow \lim _{n \rightarrow \infty}\left(4 n \tan \frac{\pi}{n}\right)=4 \pi \quad \text { A1 }
\end{aligned}
$$
A1
A1
Note: Award a maximum of M1A1AO if $\lim _{n \rightarrow \infty}$ is not stated anywhere.
[3 marks]
e.ii. $($ as $n \rightarrow \infty, P \rightarrow 4 \pi$ and $A \rightarrow 4 \pi)$
the polygon becomes a circle of radius 2
$R 1$
Note: Award $\boldsymbol{R} \boldsymbol{1}$ for alternative responses such as: the polygon becomes a circle of area $4 \pi \mathrm{OR}$ the polygon becomes a circle of perimeter $4 \pi \mathrm{OR}$ the polygon becomes a circle with $A=P=4 \pi$. Award $\boldsymbol{R O}$ for polygon becomes a circle.
[1 mark]
f. $A=\frac{1}{2} a b$ and $P=a+b+\sqrt{a^2+b^2}$
equates their expressions for $A$ and $P$
$$
\begin{aligned}
& A=P \Rightarrow a+b+\sqrt{a^2+b^2}=\frac{1}{2} a b \\
& \sqrt{a^2+b^2}=\frac{1}{2} a b-(a+b) \quad \text { M1 }
\end{aligned}
$$
(A1)(A1)
$M 1$
Note: Award $\boldsymbol{M} \boldsymbol{1}$ for isolating $\sqrt{a^2+b^2}$ or $\pm 2 \sqrt{a^2+b^2}$. This step may be seen later.
$$
\begin{aligned}
& a^2+b^2=\left(\frac{1}{2} a b-(a+b)\right)^2 \\
& a^2+b^2=\frac{1}{4} a^2 b^2-2\left(\frac{1}{2} a b\right)(a+b)+(a+b)^2 \\
& \left(=\frac{1}{4} a^2 b^2-a^2 b-a b^2+a^2+2 a b+b^2\right)
\end{aligned}
$$
Note: Award M1 for attempting to expand their RHS of either $a^2+b^2=\ldots$ or $4\left(a^2+b^2\right)=\ldots$
EITHER
$$
\begin{aligned}
& a b\left(\frac{1}{4} a b-a-b+2\right)=0(a b \neq 0) \quad \text { A1 } \\
& \frac{1}{4} a b-a-b+2=0 \\
& a b-4 a=4 b-8
\end{aligned}
$$
OR
$$
\begin{aligned}
& \frac{1}{4} a^2 b^2-a^2 b-a b^2+2 a b=0 \\
& a\left(\frac{1}{4} b^2-b\right)+\left(2 b-b^2\right)=0\left(a\left(b^2-4 b\right)+\left(8 b-4 b^2\right)=0\right) \quad \text { A1 } \\
& a=\frac{4 b^2-8 b}{b^2-4 b}
\end{aligned}
$$
THEN
$$
\begin{aligned}
& \Rightarrow a=\frac{4 b-8}{b-4} \quad \text { A1 } \\
& a=\frac{4 b-16+8}{b-4} \\
& a=\frac{8}{b-4}+4 \quad \text { AG }
\end{aligned}
$$
Note: Award a maximum of A1A1M1M1MOAOAO for attempting to verify. For example, verifying that $A=P=\frac{16}{b-4}+2 b+4$ gains 4 of the 7 marks.
For example, verifying that $A=P=\frac{16}{b-4}+2 b+4$ gains 4 of the 7 marks.
[7 marks]
g.i. using an appropriate method
(M1)
eg substituting values for $b$ or using divisibility properties
$(5,12,13)$ and $(6,8,10) \quad$ A1A1
Note: Award $A 1 A 0$ for either one set of three correct side lengths or two sets of two correct side lengths.
[3 marks]
g.ii $A=P=30$ and $A=P=24$
A1
Note: Do not award A1FT.
[1 mark]