Question Nov 2016
Let $A$ be the set $\{x \mid x \in \mathrm{R}, x \neq 0\}$. Let $B$ be the set $\{x \mid x \in]-1,+1[, x \neq 0\}$.
A function $f: A \rightarrow B$ is defined by $f(x)=\frac{2}{\pi} \arctan (x)$.
Let $D$ be the set $\{x \mid x \in \mathrm{R}, x>0\}$.
A function $g: \mathrm{R} \rightarrow D$ is defined by $g(x)=\mathrm{e}^x$.
a. (i) Sketch the graph of $y=f(x)$ and hence justify whether or not $f$ is a bijection.
[13]
(ii) Show that $A$ is a group under the binary operation of multiplication.
(iii) Give a reason why $B$ is not a group under the binary operation of multiplication.
(iv) Find an example to show that $f(a \times b)=f(a) \times f(b)$ is not satisfied for all $a, b \in A$.
b. (i) Sketch the graph of $y=g(x)$ and hence justify whether or not $g$ is a bijection.
[8]
(ii) Show that $g(a+b)=g(a) \times g(b)$ for all $a, b \in \mathrm{R}$.
(iii) Given that $\{\mathrm{R},+\}$ and $\{D, \times\}$ are both groups, explain whether or not they are isomorphic.
▶️Answer/Explanation
a.i.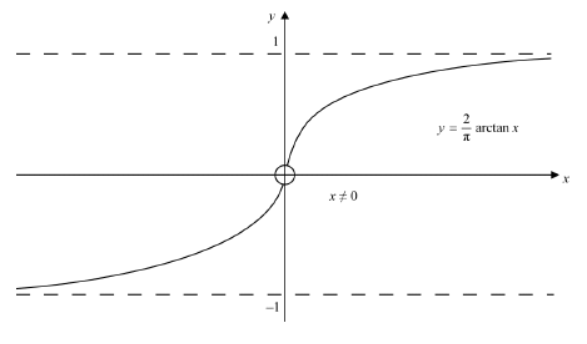
Notes: Award $\boldsymbol{A} 1$ for general shape, labelled asymptotes, and showing that $x \neq 0$.
graph shows that it is injective since it is increasing or by the horizontal line test $\boldsymbol{R} \mathbf{1}$ graph shows that it is surjective by the horizontal line test $\quad$ R1
Note: Allow any convincing reasoning.
so $f$ is a bijection $\boldsymbol{A 1}$
(ii) closed since non-zero real times non-zero real equals non-zero real $\boldsymbol{A 1 R 1}$ we know multiplication is associative R1 identity is $1 \quad \boldsymbol{A 1}$
inverse of $x$ is $\frac{1}{x}(x \neq 0) \quad \boldsymbol{A 1}$ hence it is a group $A G$
(iii) $B$ does not have an identity $\boldsymbol{A} 2$ hence it is not a group $\boldsymbol{A G}$
(iv) $f(1 \times 1)=f(1)=\frac{1}{2}$ whereas $f(1) \times f(1)=\frac{1}{2} \times \frac{1}{2}=\frac{1}{4}$ is one counterexample $\quad$ A2 hence statement is not satisfied $\boldsymbol{A G}$ [13 marks]
b.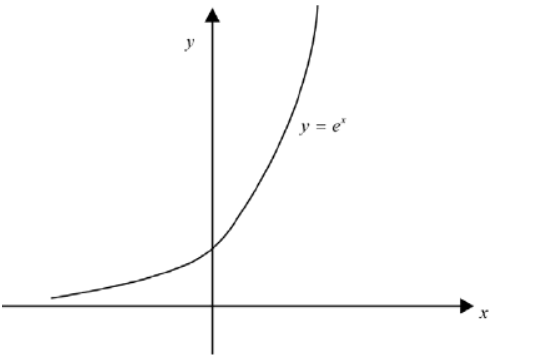
award $\boldsymbol{A} 1$ for general shape going through $(0,1)$ and with domain $\mathrm{R} \quad \boldsymbol{A} \boldsymbol{1}$
graph shows that it is injective since it is increasing or by the horizontal line test and graph shows that it is surjective by the horizontal line test
R1
Note: Allow any convincing reasoning.
so $g$ is a bijection $\quad \boldsymbol{A 1}$
(ii) $g(a+b)=\mathrm{e}^{a+b}$ and $g(a) \times g(b)=\mathrm{e}^a \times \mathrm{e}^b=\mathrm{e}^{a+b} \quad$ MIA1
hence $g(a+b)=g(a) \times g(b) \quad A G$
(iii) since $g$ is a bijection and the homomorphism rule is obeyed R1R1
the two groups are isomorphic $\boldsymbol{A 1}$
[8 marks]
Question nov 2018
Consider the functions $f, g: \mathrm{R} \times \mathrm{R} \rightarrow \mathrm{R} \times \mathrm{R}$ defined by
$$
f((x, y))=(x+y, x-y) \text { and } g((x, y))=(x y, x+y) .
$$
a.i. Find $(f \circ g)((x, y))$.
a.ii.Find $(g \circ f)((x, y))$.
b. State with a reason whether or not $f$ and $g$ commute.
c. Find the inverse of $f$.
▶️Answer/Explanation
Markscheme
$$
\begin{aligned}
& \text { a.i. }(f \circ g)((x, y))=f(g((x, y)))(=f((x y, x+y))) \\
& =(x y+x+y, x y-x-y) \quad \text { A1A1 }
\end{aligned}
$$
A1A1
[3 marks]
$$
\text { a.ii. } \begin{aligned}
& (\circ f)((x, y))=g(f((x, y))) \\
& =g((x+y, x-y)) \\
= & ((x+y)(x-y), x+y+x-y) \\
= & \left(x^2-y^2, 2 x\right) \quad \text { A1A1 }
\end{aligned}
$$
A1A1
(M1)
A1A1
[2 marks]
b. no because $f \circ g \neq g \circ f \quad \boldsymbol{R} 1$
Note: Accept counter example.
[1 mark]
C.
$$
f((x, y))=(a, b) \Rightarrow(x+y, x-y)=(a, b)
$$
(M1)
$$
\left\{\begin{array}{l}
x=\frac{a+b}{2} \\
y=\frac{a-b}{2}
\end{array}\right.
$$
(M1)
$$
f^{-1}((x, y))=\left(\frac{x+y}{2}, \frac{x-y}{2}\right)
$$
A1
[3 marks]