Question
This question investigates the sum of sine and cosine functions
The expression $3 \sin x+4 \cos x$ can be written in the form $A \cos (B x+C)+D$, where $A, B \in \mathrm{R}^{+}$and $C, D \in \mathrm{R}$ and $-\pi<C \leqslant \pi$.
The expression $5 \sin x+12 \cos x$ can be written in the form $A \cos (B x+C)+D$, where $A, B \in \mathrm{R}^{+}$and $C, D \in \mathrm{R}$ and $-\pi<C \leqslant \pi$.
In general, the expression $a \sin x+b \cos x$ can be written in the form $A \cos (B x+C)+D$, where $a, b, A, B \in \mathrm{R}^{+}$and $C, D \in \mathrm{R}$ and $-\pi<C \leqslant \pi$.
Conjecture an expression, in terms of $a$ and $b$, for
The expression $a \sin x+b \cos x$ can also be written in the form $\sqrt{a^2+b^2}\left(\frac{a}{\sqrt{a^2+b^2}} \sin x+\frac{b}{\sqrt{a^2+b^2}} \cos x\right)$.
Let $\frac{a}{\sqrt{a^2+b^2}}=\sin \theta$
a.i. Sketch the graph $y=3 \sin x+4 \cos x$, for $-2 \pi \leqslant x \leqslant 2 \pi$
a.ii.Write down the amplitude of this graph
a.iiWrite down the period of this graph
b.i. Use your answers from part (a) to write down the value of $A, B$ and $D$.
b.ii.Find the value of $C$.
c.i. Find $\arctan \frac{3}{4}$, giving the answer to 3 significant figures.
c.ii.Comment on your answer to part (c)(i).
d. By considering the graph of $y=5 \sin x+12 \cos x$, find the value of $A, B, C$ and $D$.
e.i. $A$.
e.ii $B$.
e.iiiC.
e.ivD.
f.i. Show that $\frac{b}{\sqrt{a^2+b^2}}=\cos \theta$.
f.ii. Show that $\frac{a}{b}=\tan \theta$.
g. Hence prove your conjectures in part (e).
[6]
▶️Answer/Explanation
Markscheme
a.i.
a.ii: $5 \quad$ A1
[1 mark]
a.iii2 $\pi \quad$ A1
[1 mark]
b.i. $A=5, B=1, D=0$
A1
[1 mark]
b.iimaximum at $x=0.644 \quad$ M1
So $C=-0.644$
A1
[2 marks]
c.i. 0.644
A1
[1 mark]
c.ii.it appears that $C=-\arctan \frac{3}{4}$
A1
[1 mark]
d.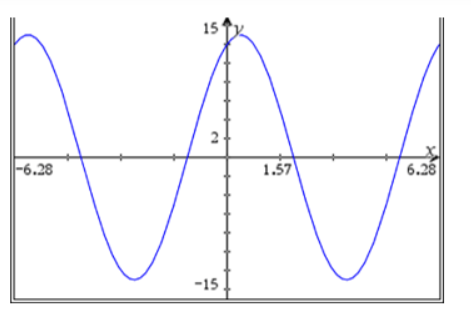
$A=13$
A1
$B=1$ and $D=0$
$A 1$
maximum at $x=0.395$
$M 1$
So $C=-0.395\left(=-\arctan \frac{5}{12}\right)$
A1
[5 marks]
e.i. $A=\sqrt{a^2+b^2}$
A1
[1 mark]
e.ii $B=1$
A1
[1 mark]
e.iiiC $=-\arctan \frac{a}{b}$
A1
[1 mark]
e.ivD $=0$
A1
[1 mark]
f.i. EITHER
use of a right triangle and Pythgoras’ to show the missing side length is $b$
M1A1
OR
Use of $\sin ^2 \theta+\cos ^2 \theta=1$, leading to the required result
M1A1
[2 marks]
f.ii. EITHER
use of a right triangle, leading to the required result.
M1
OR
Use of $\tan \theta=\frac{\sin \theta}{\cos \theta}$, leading to the required result. $\boldsymbol{M} 1$
[1 mark]
g. $a \sin x+b \cos x=\sqrt{a^2+b^2}(\sin \theta \sin x+\cos \theta \cos x) \quad$ M1
$a \sin x+b \cos x=\sqrt{a^2+b^2}(\cos (x-\theta)) \quad$ M1A1
So $A=\sqrt{a^2+b^2}, B=1$ and $D=0$
A1
And $C=-\theta \quad$ M1
So $C=-\arctan _{\frac{a}{b}} \quad$ A1
[6 marks]