Question
This question asks you to explore properties of a family of curves of the type $y^2=x^3+a x+b$ for various values of $a$ and $b$, where $a, b \in \mathbb{N}$.
On the same set of axes, sketch the following curves for $-2 \leq x \leq 2$ and $-2 \leq y \leq 2$, clearly indicating any points of intersection with the coordinate axes.
Now, consider curves of the form $y^2=x^3+b$, for $x \geq-\sqrt[3]{b}$, where $b \in \mathrm{Z}^{+}$.
Next, consider the curve $y^2=x^3+x, x \geq 0$.
The curve $y^2=x^3+x$ has two points of inflexion. Due to the symmetry of the curve these points have the same $x$-coordinate.
$\mathrm{P}(x, y)$ is defined to be a rational point on a curve if $x$ and $y$ are rational numbers.
The tangent to the curve $y^2=x^3+a x+b$ at a rational point $\mathrm{P}$ intersects the curve at another rational point $\mathrm{Q}$.
Let $C$ be the curve $y^2=x^3+2$, for $x \geq-\sqrt[3]{2}$. The rational point $\mathrm{P}(-1,-1)$ lies on $C$.
a.i. $y^2=x^3, x \geq 0$
a.ii $y^2=x^3+1, x \geq-1$
b.i. Write down the coordinates of the two points of inflexion on the curve $y^2=x^3+1$.
b.ii.By considering each curve from part (a), identify two key features that would distinguish one curve from the other.
c. By varying the value of $b$, suggest two key features common to these curves.
d.i. Show that $\frac{d y}{d x}= \pm \frac{3 x^2+1}{2 \sqrt{x^3+x}}$, for $x>0$.
d.iiHence deduce that the curve $y^2=x^3+x$ has no local minimum or maximum points.
e. Find the value of this $x$-coordinate, giving your answer in the form $x=\sqrt{\frac{p \sqrt{3}+q}{r}}$, where $p, q, r \in \mathbb{Z}$.
f.i. Find the equation of the tangent to $C$ at $P$.
f.ii. Hence, find the coordinates of the rational point $\mathrm{Q}$ where this tangent intersects $C$, expressing each coordinate as a fraction.
g. The point $\mathrm{S}(-1,1)$ also lies on $C$. The line [QS] intersects $C$ at a further point. Determine the coordinates of this point.
▶️Answer/Explanation
Markscheme
a.i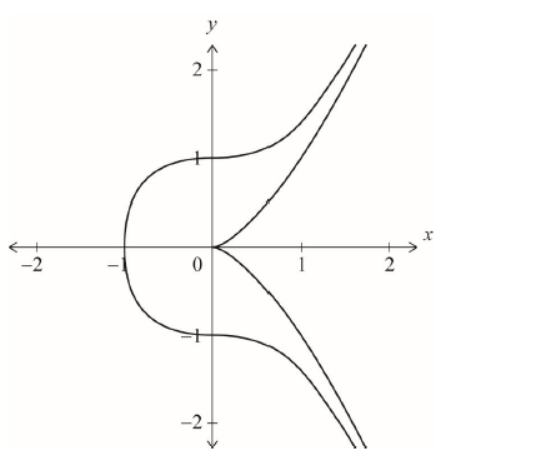
approximately symmetric about the $x$-axis graph of $y^2=x^3$
$A 1$
including cusp/sharp point at $(0,0)$
A1
[2 marks]
Note: Final $\boldsymbol{A 1}$ can be awarded if intersections are in approximate correct place with respect to the axes shown. Award $A 1 A 1 A 1 A 0$ if graphs ‘merge’ or ‘cross’ or are discontinuous at $x$-axis but are otherwise correct. Award A1AOAOAO if only one correct branch of both curves are seen.
Note: If they sketch graphs on separate axes, award a maximum of 2 marks for the ‘best’ response seen. This is likely to be A1A1AOAO.
a.iiapproximately symmetric about the $x$-axis graph of $y^2=x^3+1$ with approximately correct gradient at axes intercepts
A1
some indication of position of intersections at $x=-1, y= \pm 1$
A1
[2 marks]
Note: Final $\boldsymbol{A} \mathbf{1}$ can be awarded if intersections are in approximate correct place with respect to the axes shown. Award $\boldsymbol{A 1 A 1 A 1 A O}$ if graphs ‘merge’ or ‘cross’ or are discontinuous at $x$-axis but are otherwise correct. Award $A 1 A O A O A O$ if only one correct branch of both curves are seen.
Note: If they sketch graphs on separate axes, award a maximum of 2 marks for the ‘best’ response seen. This is likely to be $\boldsymbol{A 1 A 1 A O A O .}$
a.iiapproximately symmetric about the $x$-axis graph of $y^2=x^3+1$ with approximately correct gradient at axes intercepts
A1
some indication of position of intersections at $x=-1, y= \pm 1$
A1
[2 marks]
Note: Final $\boldsymbol{A} 1$ can be awarded if intersections are in approximate correct place with respect to the axes shown. Award $\boldsymbol{A 1 A 1 A 1 A O}$ if graphs ‘merge’ or ‘cross’ or are discontinuous at $x$-axis but are otherwise correct. Award $A 1 A O A O A O$ if only one correct branch of both curves are seen.
Note: If they sketch graphs on separate axes, award a maximum of 2 marks for the ‘best’ response seen. This is likely to be $\boldsymbol{A 1 A 1 A O A O}$.
b.i. $(0,1)$ and $(0,-1) \quad \boldsymbol{A 1}$
[1 mark]
b.ii Any two from:
$y^2=x^3$ has a cusp/sharp point, (the other does not)
graphs have different domains
$y^2=x^3+1$ has points of inflexion, (the other does not)
graphs have different $x$-axis intercepts (one goes through the origin, and the other does not)
graphs have different $y$-axis intercepts
A1
Note: Follow through from their sketch in part (a)(i). In accordance with marking rules, mark their first two responses and ignore any subsequent.
[1 mark]
c. Any two from:
as, $x \rightarrow \infty, y \rightarrow \pm \infty$
as $x \rightarrow \infty, y^2=x^3+b$ is approximated by $y^2=x^3$ (or similar)
they have $x$ intercepts at $x=-\sqrt[3]{b}$
they have $y$ intercepts at $y=( \pm) \sqrt{b}$
they all have the same range
$y=0$ (or $x$-axis) is a line of symmetry
they all have the same line of symmetry $(y=0)$
they have one $x$-axis intercept
they have two $y$-axis intercepts
they have two points of inflexion
at $x$-axis intercepts, curve is vertical/infinite gradient
there is no cusp/sharp point at $x$-axis intercepts
A1A1
Note: The last example is the only valid answer for things “not” present. Do not credit an answer of “they are all symmetrical” without some reference to the line of symmetry.
Note: Do not allow same/ similar shape or equivalent.
Note: In accordance with marking rules, mark their first two responses and ignore any subsequent.
d.i.METHOD 1
attempt to differentiate implicitly
$M 1$
$$
\begin{aligned}
& 2 y \frac{\mathrm{d} y}{\mathrm{~d} x}=3 x^2+1 \quad \text { A1 } \\
& \frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{3 x^2+1}{2 y} \text { OR }( \pm) 2 \sqrt{x^3+x} \frac{\mathrm{d} y}{\mathrm{~d} x}=3 x^2+1 \\
& \frac{\mathrm{d} y}{\mathrm{~d} x}= \pm \frac{3 x^2+1}{2 \sqrt{x^3+x}} \quad \text { AG }
\end{aligned}
$$
A1
A1
METHOD 2
attempt to use chain rule $y=( \pm) \sqrt{x^3+x} \quad$ M1
$$
\frac{\mathrm{d} y}{\mathrm{~d} x}=( \pm) \frac{1}{2}\left(x^3+x\right)^{-\frac{1}{2}}\left(3 x^2+1\right) \quad \text { A1A1 }
$$
Note: Award $\boldsymbol{A} \boldsymbol{1}$ for $( \pm) \frac{1}{2}\left(x^3+x\right)^{-\frac{1}{2}}, \boldsymbol{A} \boldsymbol{1}$ for $\left(3 x^2+1\right)$
$$
\frac{\mathrm{d} y}{\mathrm{~d} x}= \pm \frac{3 x^2+1}{2 \sqrt{x^3+x}} \quad \text { AG }
$$
[3 marks]
d.ii.EITHER
local minima/maxima occur when $\frac{\mathrm{d} y}{\mathrm{~d} x}=0$
$1+3 x^2=0$ has no (real) solutions (or equivalent) $\quad \boldsymbol{R} \mathbf{r}$
OR
$$
\left(x^2 \geq 0 \Rightarrow\right) 3 x^2+1>0, \text { so } \frac{\mathrm{d} y}{\mathrm{~d} x} \neq 0 \quad \text { R1 }
$$
THEN
so, no local minima/maxima exist $\boldsymbol{A G}$
[1 mark]
e. EITHER
attempt to use quotient rule to find $\frac{\mathrm{d}^2 y}{\mathrm{dx}^2} \quad M 1$
$$
\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}=( \pm) \frac{12 x \sqrt{x+x^3}-\left(1+3 x^2\right)\left(x+x^3\right)^{-\frac{1}{2}}\left(1+3 x^2\right)}{4\left(x+x^3\right)} \quad \text { A1A1 }
$$
Note: Award $\boldsymbol{A} 1$ for correct $12 x \sqrt{x+x^3}$ and correct denominator, $\boldsymbol{A} 1$ for correct $-\left(1+3 x^2\right)\left(x+x^3\right)^{-\frac{1}{2}}\left(1+3 x^2\right)$.
Note: Future $\boldsymbol{A}$ marks may be awarded if the denominator is missing or incorrect.
stating or using $\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}=0$ (may be seen anywhere)
(M1)
$$
12 x \sqrt{x+x^3}=\left(1+3 x^2\right)\left(x+x^3\right)^{-\frac{1}{2}}\left(1+3 x^2\right)
$$
OR
attempt to use product rule to find $\frac{d^2 y}{d x^2} \quad M 1$
$$
\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}=\frac{1}{2}\left(3 x^2+1\right)\left(-\frac{1}{2}\right)\left(3 x^2+1\right)\left(x^3+x\right)^{-\frac{3}{2}}+3 x\left(x^3+x\right)^{-\frac{1}{2}}
$$
A1A1
Note: Award $\boldsymbol{A} \mathbf{1}$ for correct first term, $\boldsymbol{A} \mathbf{1}$ for correct second term.
setting $\frac{d^2 y}{d x^2}=0$
(M1)
OR
attempts implicit differentiation on $2 y \frac{d y}{d x}=3 x^2+1 \quad$ M1
$2\left(\frac{\mathrm{d} y}{\mathrm{~d} x}\right)^2+2 y \frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}=6 x$
A1
recognizes that $\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}=0$
(M1)
$$
\begin{aligned}
& \frac{\mathrm{d} y}{\mathrm{~d} x}= \pm \sqrt{3 x} \\
& ( \pm) \frac{3 x^2+1}{2 \sqrt{x^3+x}}=( \pm) \sqrt{3 x}
\end{aligned}
$$
THEN
$$
\begin{aligned}
& 12 x\left(x+x^3\right)=\left(1+3 x^2\right)^2 \\
& 12 x^2+12 x^4=9 x^4+6 x^2+1 \\
& 3 x^4+6 x^2-1=0 \quad \text { A1 }
\end{aligned}
$$
A1
attempt to use quadratic formula or equivalent
(M1)
$x^2=\frac{-6 \pm \sqrt{48}}{6}$
$$
(x>0 \Rightarrow) x=\sqrt{\frac{2 \sqrt{3}-3}{3}}(p=2, q=-3, r=3)
$$
A1
Note: Accept any integer multiple of $p, q$ and $r$ (e.g. 4, $\quad-6$ and 6).
[7 marks]
f.i. attempt to find tangent line through $(-1,-1)$
(M1)
$y+1=-\frac{3}{2}(x+1)$ OR $y=-1.5 x-2.5 \quad$ A1
[2 marks]
f.ii. attempt to solve simultaneously with $y^2=x^3+2$
(M1)
Note: The $\boldsymbol{M} 1$ mark can be awarded for an unsupported correct answer in an incorrect format (e.g. (4. 25, – 8. 875)).
obtain $\left(\frac{17}{4},-\frac{71}{8}\right)$
A1
[2 marks]
g. attempt to find equation of [QS]
(M1)
$$
\frac{y-1}{x+1}=-\frac{79}{42}(=-1.88095 \ldots)
$$
solve simultaneously with $y^2=x^3+2$
(M1)
$x=0.28798 \ldots\left(=\frac{127}{441}\right) \quad$ A1
$y=-1.4226 \ldots\left(=\frac{13175}{9261}\right) \quad \boldsymbol{A 1}$
$(0.228,-1.42)$
OR
attempt to find vector equation of [QS]
(M1)
$$
\begin{aligned}
& \left(\begin{array}{l}
x \\
y
\end{array}\right)=\left(\begin{array}{c}
-1 \\
1
\end{array}\right)+\lambda\left(\begin{array}{c}
\frac{21}{4} \\
-\frac{79}{8}
\end{array}\right) \\
& x=-1+\frac{21}{4} \lambda \\
& y=1-\frac{79}{8} \lambda
\end{aligned}
$$
(A1)
attempt to solve $\left(1-\frac{79}{8} \lambda\right)^2=\left(-1+\frac{21}{4} \lambda\right)^3+2 \quad$ (M1)
$$
\lambda=0.2453 \ldots
$$
$x=0.28798 \ldots\left(=\frac{127}{441}\right) \quad \boldsymbol{A 1}$
$y=-1.4226 \ldots\left(=\frac{13175}{9261}\right) \quad$ A1
(0.228, – 1.42)
[5 marks]