Question
a. Find the value of $\int_4^{\infty} \frac{1}{x^3} \mathrm{~d} x$.
[3]
b. Illustrate graphically the inequality $\sum_{n=5}^{\infty} \frac{1}{n^3}<\int_4^{\infty} \frac{1}{x^3} \mathrm{~d} x<\sum_{n=4}^{\infty} \frac{1}{n^3}$ I
c. Hence write down a lower bound for $\sum_{n=4}^{\infty} \frac{1}{n^3}$.
d. Find an upper bound for $\sum_{n=4}^{\infty} \frac{1}{n^3}$.
▶️Answer/Explanation
Markscheme
a. * This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
$$
\int_4^{\infty} \frac{1}{x^3} \mathrm{~d} x=\lim _{R \rightarrow \infty} \int^R \frac{1}{x^3} \mathrm{~d} x
$$
(A1)
Note: The above $\boldsymbol{A} 1$ for using a limit can be awarded at any stage.
Condone the use of $\lim _{x \rightarrow \infty}$.
Do not award this mark to candidates who use $\infty$ as the upper limit throughout.
$$
\begin{aligned}
& =\lim _{R \rightarrow \infty}\left[-\frac{1}{2} x^{-2}\right]_4^R\left(=\left[-\frac{1}{2} x^{-2}\right]_4^{\infty}\right) \quad \text { M1 } \\
& =\lim _{R \rightarrow \infty}\left(-\frac{1}{2}\left(R^{-2}-4^{-2}\right)\right) \\
& =\frac{1}{32} \quad \boldsymbol{A 1}
\end{aligned}
$$
[3 marks]
b.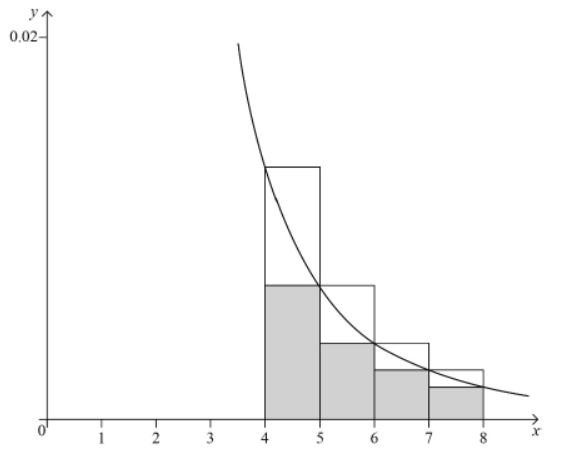
A1 for the curve
A1 for rectangles starting at $x=4$
$\boldsymbol{A 1}$ for at least three upper rectangles
$\boldsymbol{A 1}$ for at least three lower rectangles
Note: Award $\boldsymbol{A O A 1}$ for two upper rectangles and two lower rectangles.
sum of areas of the lower rectangles < the area under the curve < the sum of the areas of the upper rectangles so
$$
\sum_{n=5}^{\infty} \frac{1}{n^3}<\int_4^{\infty} \frac{1}{x^3} \mathrm{~d} x<\sum_{n=4}^{\infty} \frac{1}{n^3} \quad \text { AG }
$$
[4 marks]
c. a lower bound is $\frac{1}{32} \quad \boldsymbol{A 1}$
Note: Allow FT from part (a).
[1 mark]
d. METHOD 1
$$
\begin{aligned}
& \sum_{n=5}^{\infty} \frac{1}{n^3}<\frac{1}{32} \quad \text { (M1) } \\
& \frac{1}{64}+\sum_{n=5}^{\infty} \frac{1}{n^3}=\frac{1}{32}+\frac{1}{64}
\end{aligned}
$$
(M1)
$\frac{1}{64}+\sum_{n=5}^{\infty} \frac{1}{n^3}=\frac{1}{32}+\frac{1}{64}$
(M1)
$\sum_{n=4}^{\infty} \frac{1}{n^3}<\frac{3}{64}$, an upper bound
A1
Note: Allow $\boldsymbol{F T}$ from part (a).
METHOD 2
changing the lower limit in the inequality in part (b) gives
$\sum_{n=4}^{\infty} \frac{1}{n^3}<\int_3^{\infty} \frac{1}{x^3} \mathrm{dx}\left(<\sum_{n=3}^{\infty} \frac{1}{n^3}\right)$
(A1)
$\sum_{n=4}^{\infty} \frac{1}{n^3}<\lim _{R \rightarrow \infty}\left[-\frac{1}{2} x^{-2}\right]_3^R$
(M1)
$\sum_{n=4}^{\infty} \frac{1}{n^3}<\frac{1}{18}$, an upper bound
A1
Note: Condone candidates who do not use a limit.
[3 marks]