Question: [Maximum mark: 5]
The derivative of a function g is given by g ′(x) = 3x2 + 5ex, where x ∈ R. The graph of g passes through the point (0, 4). Find g(x).
Answer/Explanation
Ans:
METHOD 1
recognises that \(g(x)= \int \left ( 3x^{2} +5e^{x}\right )dx\)
\(g(x)= x^{3}+5e^{x}(+C)\)
Note: Award A1 for each integrated term.
substitutes x = 0 and y = 4 into their integrated function (must involve +C)
4 = 0 + 5 + C ⇒ C = -1
\(g(x)= x^{3}+5e^{x}-1\)
METHOD 2
attempts to write both sides in the form of a definite integral
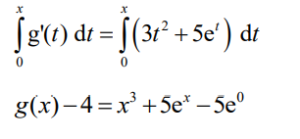
Note: Award A1 for g x( ) 4 − and A1 for \(x^{3}+5e^{x}-5e^{0}.
\(g(x)= x^{3}+5e^{x}-1\)
Question
Find ∫(6x +7) dx . [3]
Given f ′(x) = 6x + 7 and f (1.2) = 7.32, , find f (x) [3]
Answer/Explanation
Ans:
(a) correct integration 3x2+ 7x+ c
(b)
recognition that f(x)= ∫ f'(x)dx
\(3(1.2)^{2}+ 7(1.2)+ c= 7.32\)
c= -5.4
\(f (x)= 3x^{2}+ 7x-5.4\)
Question
By using the substitution \(x = 2\tan u\), show that \(\int {\frac{{{\text{d}}x}}{{{x^2}\sqrt {{x^2} + 4} }} = \frac{{ – \sqrt {{x^2} + 4} }}{{4x}} + C} \).
Answer/Explanation
Markscheme
EITHER
\(\frac{{{\text{d}}x}}{{{\text{d}}u}} = 2\,{\text{se}}{{\text{c}}^2}u\) A1
\(\int {\frac{{2\,{\text{se}}{{\text{c}}^2}u{\text{d}}u}}{{4{{\tan }^2}u\sqrt {4 + 4{{\tan }^2}u} }}} \) (M1)
\(\int {\frac{{2\,{\text{se}}{{\text{c}}^2}u{\text{d}}u}}{{4{{\tan }^2}u \times 2\,\sec u}}} \) \(( = \int {\frac{{{\text{d}}u}}{{4{{\sin }^2}u\sqrt {{{\tan }^2}u + 1} }}{\text{ or }} = \int {\frac{{2\,{\text{se}}{{\text{c}}^2}u{\text{d}}u}}{{4{{\tan }^2}u\sqrt {4{{\sec }^2}u} }})} } \) A1
OR
\(u = \arctan \frac{x}{2}\)
\(\frac{{{\text{d}}u}}{{{\text{d}}x}} = \frac{2}{{{x^2} + 4}}\) A1
\(\int {\frac{{\sqrt {4{{\tan }^2}u + 4{\text{d}}u} }}{{2 \times 4{{\tan }^2}u}}} \) (M1)
\(\int {\frac{{2\,\sec u{\text{d}}u}}{{2 \times 4{{\tan }^2}u}}} \) A1
THEN
\( = \frac{1}{4}\int {\frac{{\sec u{\text{d}}u}}{{{{\tan }^2}u}}} \)
\( = \frac{1}{4}\int {{\text{cosec}}\,u\cot u{\text{d}}u{\text{ }}\left( { = \frac{1}{4}\int {\frac{{\cos u}}{{{{\sin }^2}u}}{\text{d}}u} } \right)} \) A1
\( = – \frac{1}{4}{\text{cosec}}\,u( + C){\text{ }}\left( { = – \frac{1}{{4\sin u}}( + C)} \right)\) A1
use of either \(u = \frac{x}{2}\) or an appropriate trigonometric identity M1
either \(\sin u = \frac{x}{{\sqrt {{x^2} + 4} }}\) or \({\text{cosec}}\,u = \frac{{\sqrt {{x^2} + 4} }}{x}\) (or equivalent) A1
\( = \frac{{ – \sqrt {{x^2} + 4} }}{{4x}}( + C)\) AG
[7 marks]
Examiners report
Most candidates found this a challenging question. A large majority of candidates were able to change variable from x to u but were not able to make any further progress.
Question
Given that \(2{x^3} – 3x + 1\) can be expressed in the form \(Ax\left( {{x^2} + 1} \right) + Bx + C\), find the values of the constants \(A\), \(B\) and \(C\).
Hence find \(\int {\frac{{2{x^3} – 3x + 1}}{{{x^2} + 1}}} {\text{d}}x\).
Answer/Explanation
Markscheme
\(2{x^3} – 3x + 1 = Ax\left( {{x^2} + 1} \right) + Bx + C\)
\(A = 2,\,\,C = 1,\) A1
\(A + B = – 3 \Rightarrow B = – 5\) A1
[2 marks]
\(\int {\frac{{2{x^3} – 3x + 1}}{{{x^2} + 1}}} {\text{d}}x = \int {\left( {2x – \frac{{5x}}{{{x^2} + 1}} + \frac{1}{{{x^2} + 1}}} \right)} {\text{d}}x\) M1M1
Note: Award M1 for dividing by \(\left( {{x^2} + 1} \right)\) to get \(2x\), M1 for separating the \(5x\) and 1.
\( = {x^2} – \frac{5}{2}{\text{ln}}\left( {{x^2} + 1} \right) + {\text{arctan}}\,x\left( { + c} \right)\) (M1)A1A1
Note: Award (M1)A1 for integrating \({\frac{{5x}}{{{x^2} + 1}}}\), A1 for the other two terms.
[5 marks]
Examiners report
[N/A]
[N/A]
Question
Given that \(2{x^3} – 3x + 1\) can be expressed in the form \(Ax\left( {{x^2} + 1} \right) + Bx + C\), find the values of the constants \(A\), \(B\) and \(C\).
Hence find \(\int {\frac{{2{x^3} – 3x + 1}}{{{x^2} + 1}}} {\text{d}}x\).
Answer/Explanation
Markscheme
\(2{x^3} – 3x + 1 = Ax\left( {{x^2} + 1} \right) + Bx + C\)
\(A = 2,\,\,C = 1,\) A1
\(A + B = – 3 \Rightarrow B = – 5\) A1
[2 marks]
\(\int {\frac{{2{x^3} – 3x + 1}}{{{x^2} + 1}}} {\text{d}}x = \int {\left( {2x – \frac{{5x}}{{{x^2} + 1}} + \frac{1}{{{x^2} + 1}}} \right)} {\text{d}}x\) M1M1
Note: Award M1 for dividing by \(\left( {{x^2} + 1} \right)\) to get \(2x\), M1 for separating the \(5x\) and 1.
\( = {x^2} – \frac{5}{2}{\text{ln}}\left( {{x^2} + 1} \right) + {\text{arctan}}\,x\left( { + c} \right)\) (M1)A1A1
Note: Award (M1)A1 for integrating \({\frac{{5x}}{{{x^2} + 1}}}\), A1 for the other two terms.
[5 marks]
Examiners report
[N/A]
[N/A]
