Question 6. [Maximum mark: 18]
An ice-skater is skating such that her position vector when viewed from above at time t
seconds can be modelled by
\((_{x}^{y})\) = 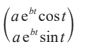
with respect to a rectangular coordinate system from a point O, where the non-zero constants a and b can be determined. All distances are in metres.
a. Find the velocity vector at time t . [3]
b. Show that the magnitude of the velocity of the ice-skater at time t is given by
\(a^{ebt}\sqrt{(1+b^{2})}\) [4]
At time t = 0 , the displacement of the ice-skater is given by \((_{0}^{5})\) and the velocity of the
ice-skater is given by ( 5 ) .
c. Find the value of a and the value of b . [3]
d. Find the magnitude of the velocity of the ice-skater when t = 2 . [2] At a point P, the ice-skater is skating parallel to the y-axis for the first time.
e. Find OP. [6]
▶️Answer/Explanation
(a) use of product rule \((_{y}^{x})= (_{abe^{bt}sin t + ae^{bt}cost t}^{abe ^{bt}cost – ae ^{bt}sin t})\)
(b) \(|v|^{2}= x^{2}+y^{2}=[abe^{bt}cost – ae^{bt}sint]^{2}+ [abe^{bt}sint+ae^{bt}cost]^{2}\)
\(= [a^{2}sin^{2}t – 2a^{2}bsin t cost + a^{2}b^{2}cos^{2}t + a^{2}cos^{2}+ 2a^{2}bsint costt +a^{2}b^{2}sin^{2}t ]\) use of \(sin^{2}t + cos^{2}t=1\)
\(=a^{2}(b^{2}+1)e^{2bt}\) magnitude of velocity is \(ae^{bt}\sqrt{(1+ b^{2})}\)
(c) when t = 0, \(ae^{bt}cost = 5 a=5 abe^{bt}cost – ae^{bt}sint = -3.5 b = -0.7\ )
(d)\(5e^{-0.7\times 2}\sqrt{(1+(-0.7)^{2})}1.51(1.50504…)\)
(e) \(x=0 ae^{bt}(b cost – simt)=0 tant=b t = 2.53 (2.53086…)\) correct substitution of their t to find x or y
\(x = − 0.697 (- 0.696591…)\) and \(y = 0.488 (0.487614…)\)
use of Pythagoras / distance formula \(OP = 0.850 m (0.850297…)\)
Question
A student investigating the relationship between chemical reactions and temperature finds
the Arrhenius equation on the internet.
\(k=Ae^{-\frac{c}{T}}\)
This equation links a variable k with the temperature T, where A and c are positive
constants and T > 0.
(a) Show that \(\frac{dk}{dT}\) is always positive. [3]
(b) Given that \(\lim_{T\rightarrow \infty }k=A \ and \ \lim_{T\rightarrow 0}k=0\), sketch the graph of k against T. [3]
The Arrhenius equation predicts that the graph of ln k against \(\frac{1}{T}\) is a straight line.
(c) Write down
(i) the gradient of this line in terms of c ;
(ii) the y-intercept of this line in terms of A. [4]
The following data are found for a particular reaction, where T is measured in Kelvin
and k is measured in cm3 mol−1 s−1:
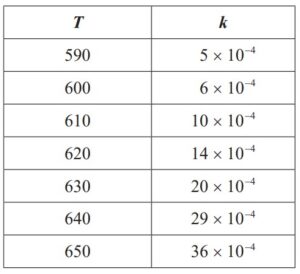
(d) Find the equation of the regression line for ln k on \(\frac{1}{T}\) [2]
(e) Find an estimate of
(i) c ;
(ii) A.
It is not required to state units for these values. [3]
▶️Answer/Explanation
Ans
4. (a) attempt to use chain rule, including the differentiation of \(\frac{1}{T}\) (M1)
\(\frac{dk}{dT}=A\times \frac{c}{T^{2}}\times e^{-\frac{c}{T}}\)
this is the product of positive quantities so must be positive R1
Note: The R1 may be awarded for correct argument from their derivative.
R1 is not possible if their derivative is not always positive.
[3 marks]
(b)
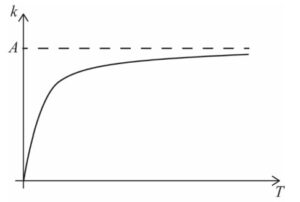
A1A1A1
Note: Award A1 for an increasing graph, entirely in first quadrant, becoming
concave down for larger values of T, A1 for tending towards the origin
and A1 for asymptote labelled at k = A .
[3 marks]
(c) taking ln of both sides OR substituting y = ln x and \(x=\frac{1}{T}\) (M1)
\(ln k=ln A=-\frac{c}{T}\ OR \ y=-cx+ln A\) (A1)
(i) so gradient is −c A1
(ii) y-intercept is ln A A1
Note: The implied (M1) and (A1) can only be awarded if both correct answers are
seen. Award zero if only one value is correct and no working is seen.
[4 marks]
continued…
(d) an attempt to convert data to \(\frac{1}{T}\) ln k (M1)
e.g. at least one correct row in the following table
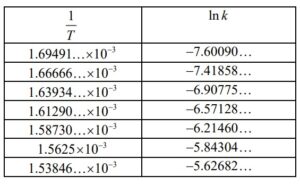
line is \(ln k=-13400\times \frac{1}{T}+15.0 \left ( =-13383.1…\times \frac{1}{T}+15.0107 \right )\) A1
[2 marks]
(e) (i) c =13400 (13383.1 ) … A1
(ii) attempt to rearrange or solve graphically ln 15.0107 A = … (M1)
A = (3300000 3304 258…) A1
Note: Accept an A value of 3269017… from use of 3sf value.
[3 marks]
Total [15 marks]
Question
A small bead is free to move along a smooth wire in the shape of the curve y = \(\frac{10}{3-2e^{-0.5x}}\) ( x ≥ 0 ).
Find an expression for \(\frac{dy}{dx}\) . [3]
At the point on the curve where x = 4 , it is given that \(\frac{dy}{dt}\)= – 0.1 m s–1.
Find the value of \(\frac{dy}{dt}\) at this exact same instant. [3]
▶️Answer/Explanation
Ans
(a) valid attempt to use chain rule or quotient rule
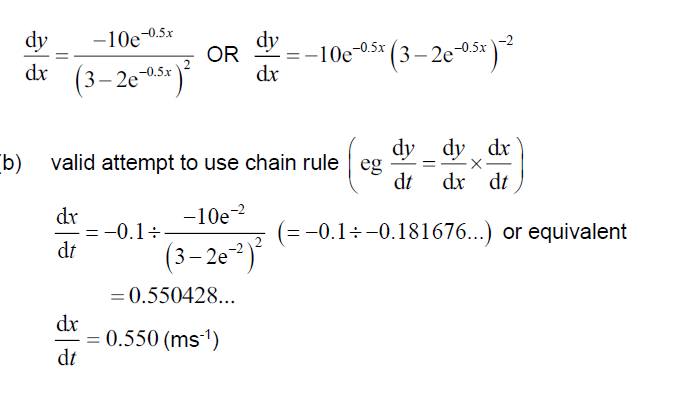
Question
The diagram shows the plan of an art gallery a metres wide. [AB] represents a doorway, leading to an exit corridor b metres wide. In order to remove a painting from the art gallery, CD (denoted by L ) is measured for various values of \(\alpha \) , as represented in the diagram.
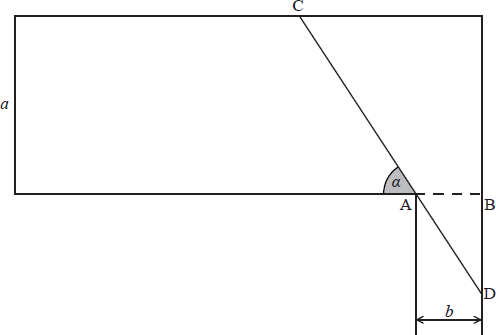
a.If \(\alpha \) is the angle between [CD] and the wall, show that \(L = \frac{a }{{\sin \alpha }} + \frac{b}{{\cos \alpha }}{\text{, }}0 < \alpha < \frac{\pi }{2}\).[3]
b.If a = 5 and b = 1, find the maximum length of a painting that can be removed through this doorway.[4]
c.Let a = 3k and b = k .
Find \(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }}\).[3]
d.Let a = 3k and b = k .
Find, in terms of k , the maximum length of a painting that can be removed from the gallery through this doorway.[6]
e.Let a = 3k and b = k .
Find the minimum value of k if a painting 8 metres long is to be removed through this doorway.[2]
▶️Answer/Explanation
Markscheme
\(L = {\text{CA}} + {\text{AD}}\) M1
\({\text{sin}}\alpha {\text{ = }}\frac{a}{{{\text{CA}}}} \Rightarrow {\text{CA}} = \frac{a}{{\sin \alpha }}\) A1
\(\cos \alpha = \frac{b}{{{\text{AD}}}} \Rightarrow {\text{AD}} = \frac{b}{{\cos \alpha }}\) A1
\(L = \frac{a}{{\sin \alpha }} + \frac{b}{{\cos \alpha }}\) AG
[2 marks]
\(a = 5{\text{ and }}b = 1 \Rightarrow L = \frac{5}{{\sin \alpha }} + \frac{1}{{\cos \alpha }}\)
METHOD 1
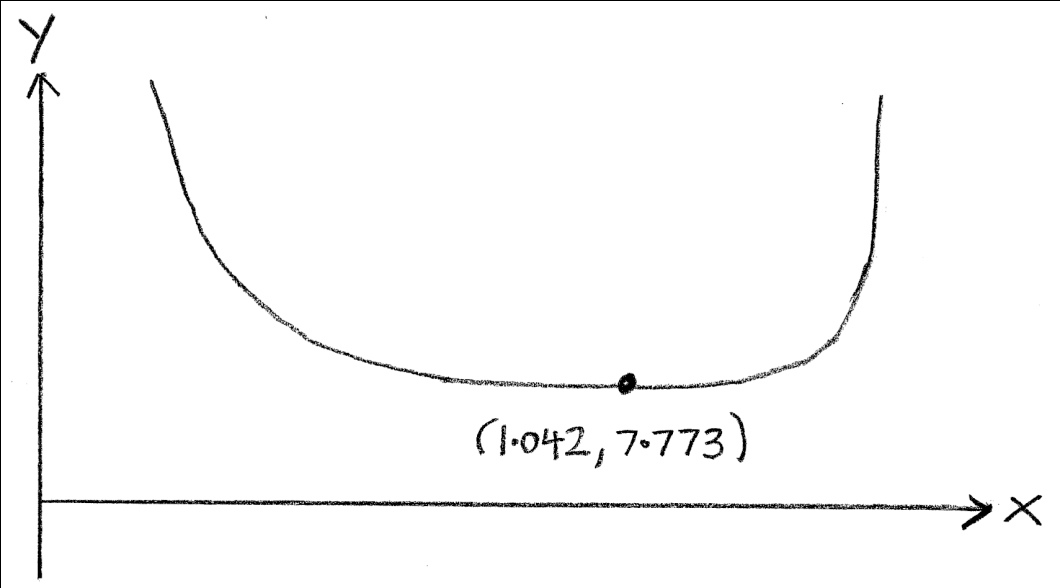 (M1)
(M1)
minimum from graph \( \Rightarrow L = 7.77\) (M1)A1
minimum of L gives the max length of the painting R1
[4 marks]
METHOD 2
\(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }} = \frac{{ – 5\cos \alpha }}{{{{\sin }^2}\alpha }} + \frac{{\sin \alpha }}{{{{\cos }^2}\alpha }}\) (M1)
\(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }} = 0 \Rightarrow \frac{{{{\sin }^3}\alpha }}{{{{\cos }^3}\alpha }} = 5 \Rightarrow \tan \alpha = \sqrt[{3{\text{ }}}]{5}{\text{ }}(\alpha = 1.0416…)\) (M1)
minimum of L gives the max length of the painting R1
maximum length = 7.77 A1
[4 marks]
\(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }} = \frac{{ – 3k\cos \alpha }}{{{{\sin }^2}\alpha }} + \frac{{k\sin \alpha }}{{{{\cos }^2}\alpha }}\,\,\,\,\,{\text{(or equivalent)}}\) M1A1A1
[3 marks]
\(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }} = \frac{{ – 3k{{\cos }^3}\alpha + k{{\sin }^3}\alpha }}{{{{\sin }^2}\alpha {{\cos }^2}\alpha }}\) (A1)
\(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }} = 0 \Rightarrow \frac{{{{\sin }^3}\alpha }}{{{{\cos }^3}\alpha }} = \frac{{3k}}{k} \Rightarrow \tan \alpha = \sqrt[3]{3}\,\,\,\,\,(\alpha = 0.96454…)\) M1A1
\(\tan \alpha = \sqrt[3]{3} \Rightarrow \frac{1}{{\cos \alpha }} = \sqrt {1 + \sqrt[3]{9}} \,\,\,\,\,(1.755…)\) (A1)
\({\text{and }}\frac{1}{{\sin \alpha }} = \frac{{\sqrt {1 + \sqrt[3]{9}} }}{{\sqrt[3]{3}}}\,\,\,\,\,(1.216…)\) (A1)
\(L = 3k\left( {\frac{{\sqrt {1 + \sqrt[3]{9}} }}{{\sqrt[3]{3}}}} \right) + k\sqrt {1 + \sqrt[3]{9}} \,\,\,\,\,(L = 5.405598…k)\) A1 N4
[6 marks]
\(L \leqslant 8 \Rightarrow k \geqslant 1.48\) M1A1
the minimum value is 1.48
[2 marks]
Examiners report
Part (a) was very well done by most candidates. Parts (b), (c) and (d) required a subtle balance between abstraction, differentiation skills and use of GDC.
In part (b), although candidates were asked to justify their reasoning, very few candidates offered an explanation for the maximum. Therefore most candidates did not earn the R1 mark in part (b). Also not as many candidates as anticipated used a graphical approach, preferring to use the calculus with varying degrees of success. In part (c), some candidates calculated the derivatives of inverse trigonometric functions. Some candidates had difficulty with parts (d) and (e). In part (d), some candidates erroneously used their alpha value from part (b). In part (d) many candidates used GDC to calculate decimal values for \(\alpha \) and L. The premature rounding of decimals led sometimes to inaccurate results. Nevertheless many candidates got excellent results in this question.
Part (a) was very well done by most candidates. Parts (b), (c) and (d) required a subtle balance between abstraction, differentiation skills and use of GDC.
In part (b), although candidates were asked to justify their reasoning, very few candidates offered an explanation for the maximum. Therefore most candidates did not earn the R1 mark in part (b). Also not as many candidates as anticipated used a graphical approach, preferring to use the calculus with varying degrees of success. In part (c), some candidates calculated the derivatives of inverse trigonometric functions. Some candidates had difficulty with parts (d) and (e). In part (d), some candidates erroneously used their alpha value from part (b). In part (d) many candidates used GDC to calculate decimal values for \(\alpha \) and L. The premature rounding of decimals led sometimes to inaccurate results. Nevertheless many candidates got excellent results in this question.
Part (a) was very well done by most candidates. Parts (b), (c) and (d) required a subtle balance between abstraction, differentiation skills and use of GDC.
In part (b), although candidates were asked to justify their reasoning, very few candidates offered an explanation for the maximum. Therefore most candidates did not earn the R1 mark in part (b). Also not as many candidates as anticipated used a graphical approach, preferring to use the calculus with varying degrees of success. In part (c), some candidates calculated the derivatives of inverse trigonometric functions. Some candidates had difficulty with parts (d) and (e). In part (d), some candidates erroneously used their alpha value from part (b). In part (d) many candidates used GDC to calculate decimal values for \(\alpha \) and L. The premature rounding of decimals led sometimes to inaccurate results. Nevertheless many candidates got excellent results in this question.
Part (a) was very well done by most candidates. Parts (b), (c) and (d) required a subtle balance between abstraction, differentiation skills and use of GDC.
In part (b), although candidates were asked to justify their reasoning, very few candidates offered an explanation for the maximum. Therefore most candidates did not earn the R1 mark in part (b). Also not as many candidates as anticipated used a graphical approach, preferring to use the calculus with varying degrees of success. In part (c), some candidates calculated the derivatives of inverse trigonometric functions. Some candidates had difficulty with parts (d) and (e). In part (d), some candidates erroneously used their alpha value from part (b). In part (d) many candidates used GDC to calculate decimal values for \(\alpha \) and L. The premature rounding of decimals led sometimes to inaccurate results. Nevertheless many candidates got excellent results in this question.
Part (a) was very well done by most candidates. Parts (b), (c) and (d) required a subtle balance between abstraction, differentiation skills and use of GDC.
In part (b), although candidates were asked to justify their reasoning, very few candidates offered an explanation for the maximum. Therefore most candidates did not earn the R1 mark in part (b). Also not as many candidates as anticipated used a graphical approach, preferring to use the calculus with varying degrees of success. In part (c), some candidates calculated the derivatives of inverse trigonometric functions. Some candidates had difficulty with parts (d) and (e). In part (d), some candidates erroneously used their alpha value from part (b). In part (d) many candidates used GDC to calculate decimal values for \(\alpha \) and L. The premature rounding of decimals led sometimes to inaccurate results. Nevertheless many candidates got excellent results in this question.
Question
The function f has inverse \({f^{ – 1}}\) and derivative \(f'(x)\) for all \(x \in \mathbb{R}\). For all functions with these properties you are given the result that for \(a \in \mathbb{R}\) with \(b = f(a)\) and \(f'(a) \ne 0\)
\[({f^{ – 1}})'(b) = \frac{1}{{f'(a)}}.\]
a.Verify that this is true for \(f(x) = {x^3} + 1\) at x = 2.[6]
b.Given that \(g(x) = x{{\text{e}}^{{x^2}}}\), show that \(g'(x) > 0\) for all values of x.[3]
c.Using the result given at the start of the question, find the value of the gradient function of \(y = {g^{ – 1}}(x)\) at x = 2.[4]
d.(i) With f and g as defined in parts (a) and (b), solve \(g \circ f(x) = 2\).
(ii) Let \(h(x) = {(g \circ f)^{ – 1}}(x)\). Find \(h'(2)\).[6]
▶️Answer/Explanation
Markscheme
\(f(2) = 9\) (A1)
\({f^{ – 1}}(x) = {(x – 1)^{\frac{1}{3}}}\) A1
\(({f^{ – 1}})'(x) = \frac{1}{3}{(x – 1)^{ – \frac{2}{3}}}\) (M1)
\(({f^{ – 1}})'(9) = \frac{1}{{12}}\) A1
\(f'(x) = 3{x^2}\) (M1)
\(\frac{1}{{f'(2)}} = \frac{1}{{3 \times 4}} = \frac{1}{{12}}\) A1
Note: The last M1 and A1 are independent of previous marks.
[6 marks]
\(g'(x) = {{\text{e}}^{{x^2}}} + 2{x^2}{{\text{e}}^{{x^2}}}\) M1A1
\(g'(x) > 0\) as each part is positive R1
[3 marks]
to find the x-coordinate on \(y = g(x)\) solve
\(2 = x{{\text{e}}^{{x^2}}}\) (M1)
\(x = 0.89605022078 \ldots \) (A1)
gradient \( = ({g^{ – 1}})'(2) = \frac{1}{{g'(0.896 \ldots )}}\) (M1)
\( = \frac{1}{{{{\text{e}}^{{{(0.896 \ldots )}^2}}}\left( {1 + 2 \times {{(0.896 \ldots )}^2}} \right)}} = 0.172\) to 3sf A1
(using the \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) function on gdc \(g'(0.896 \ldots ) = 5.7716028 \ldots \)
\(\frac{1}{{g'(0.896 \ldots )}} = 0.173\)
[4 marks]
(i) \(({x^3} + 1){{\text{e}}^{{{({x^3} + 1)}^2}}} = 2\) A1
\(x = – 0.470191 \ldots \) A1
(ii) METHOD 1
\((g \circ f)'(x) = 3{x^2}{{\text{e}}^{{{({x^3} + 1)}^2}}}\left( {2{{({x^3} + 1)}^2} + 1} \right)\) (M1)(A1)
\((g \circ f)'( – 0.470191 \ldots ) = 3.85755 \ldots \) (A1)
\(h'(2) = \frac{1}{{3.85755 \ldots }} = 0.259{\text{ }}(232 \ldots )\) A1
Note: The solution can be found without the student obtaining the explicit form of the composite function.
METHOD 2
\(h(x) = ({f^{ – 1}} \circ {g^{ – 1}})(x)\) A1
\(h'(x) = ({f^{ – 1}})’\left( {{g^{ – 1}}(x)} \right) \times ({g^{ – 1}})'(x)\) M1
\( = \frac{1}{3}{\left( {{g^{ – 1}}(x) – 1} \right)^{ – \frac{2}{3}}} \times ({g^{ – 1}})'(x)\) M1
\(h'(2) = \frac{1}{3}{\left( {{g^{ – 1}}(2) – 1} \right)^{ – \frac{2}{3}}} \times ({g^{ – 1}})'(2)\)
\( = \frac{1}{3}{(0.89605 \ldots – 1)^{ – \frac{2}{3}}} \times 0.171933 \ldots \)
\( = 0.259{\text{ }}(232 \ldots )\) A1 N4
[6 marks]
Examiners report
There were many good attempts at parts (a) and (b), although in (b) many were unable to give a thorough justification.
There were many good attempts at parts (a) and (b), although in (b) many were unable to give a thorough justification.
Few good solutions to parts (c) and (d)(ii) were seen although many were able to answer (d)(i) correctly.
Few good solutions to parts (c) and (d)(ii) were seen although many were able to answer (d)(i) correctly.
