Question: [Maximum mark: 19]
Consider the differential equation \(x^{2}\frac{dy}{dx}=y^{2}-2x^{2}\) for x > 0 and y > 2x . It is given that y = 3 when x = 1.
(a) Use Euler’s method, with a step length of 0.1, to find an approximate value of y when x = 1.5.
(b) Use the substitution y = vx to show that \(x\frac{dv}{dx}=v^{2}-v-2.\)
(c) (i) By solving the differential equation, show that \(y = \frac{8x+x^{4}}{4-x^{3}}.\)
(ii) Find the actual value of y when x = 1.5.
(iii) Using the graph of \(y = \frac{8x+x^{4}}{4-x^{3}}\) suggest a reason why the approximation given by Euler’s method in part (a) is not a good estimate to the actual value of y at x = 1.5.
▶️Answer/Explanation
Ans:
(a) attempt to use Euler’s method 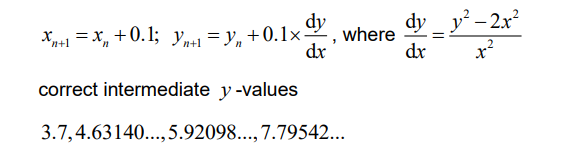
Note: A1 for any two correct y -values seen
y =10.6958…
y =10.7
Note: For the final A1, the value 10.7 must be the last value in a table or a list, or be given as a final answer, not just embedded in a table which has further lines.
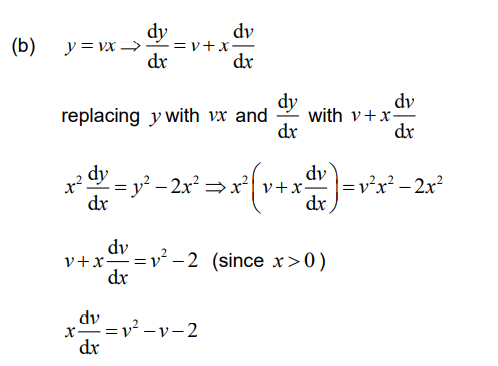
(c) (i) attempt to separate variables v and x

Note: Condone absence of modulus signs throughout.
EITHER
attempt to find c using x = 1, y = 3, v= 3
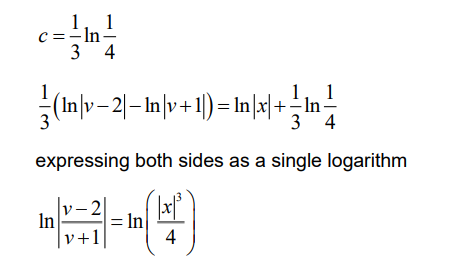
OR
expressing both sides as a single logarithm
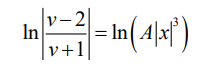
attempt to find A using x = 1, y = 3, v= 3

(ii) actual value at y(1.5) = 27.3
(iii) gradient changes rapidly (during the interval considered) OR the curve has a vertical asymptote at \(x = \sqrt[3]{4}(=1.5874…)\)
Question
Consider the curve C defined by y2 = sin ( xy ) , y ≠ 0 .
Show that \(\frac{dy}{dx}= \frac{ycos(xy)}{2y-xcos(xy)}\) [5]
Prove that, when \(\frac{dy}{dx}\) = o , y = ±[5]
Hence find the coordinates of all points on C , for 0 < x < 4π , where \(\frac{dy}{dx}\)= 0 . [5]
▶️Answer/Explanation
Ans:
(a)
attempt at implicit differentiation
2y \(\frac{dy}{dx}= cos (xy)[x\frac{dy}{dx}+y]\)
2y\(\frac{dy}{dx}-x\frac{dy}{dx}\) cos(xy)= ycos(xy)
\(\frac{dy}{dx}(2y-xcos(xy))\)= ycos(xy)
\(\frac{dy}{dx}=\frac{ycos(xy)}{2y-xcos(xy)}\)
(b)
setting \(\frac{dy}{dx}=0\)
ycos(xy)=0

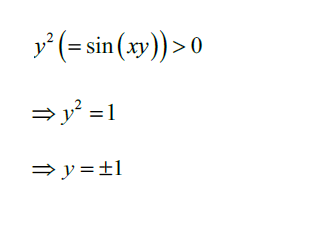
(c)

MAA HL 5.19 DIFFERENTIAL EQUATIONS-Neha
Question
The equation \(x^{2}+y^{2}=1\) defines the unit circle with its centre at the origin. The circle passes through the point (1,0).
(a) Use implicit differentiation on \(x^{2}+y^{2}=1\) to show that \(\frac{\mathrm{d} y}{\mathrm{d} x}=-\frac{x}{y}\).
(b) Solve the differential equation \(\frac{\mathrm{d} y}{\mathrm{d} x}=-\frac{x}{y}\) given that the curve passes through (1,0) to derive the equation of the unit circle.
▶️Answer/Explanation
Ans
(a) \(x^{2}+y^{2}=1\Rightarrow 2x+2y\frac{\mathrm{d} y}{\mathrm{d} x}=0\Rightarrow 2y\frac{\mathrm{d} y}{\mathrm{d} x}=-2x\Rightarrow \frac{\mathrm{d} y}{\mathrm{d} x}=-\frac{x} {y}\)
(b) \(\frac{\mathrm{d} y}{\mathrm{d} x}=-\frac{x}{y}\Rightarrow ydy=-xdx\Rightarrow \int ydy=-\int xdx\Rightarrow \frac{y^{2}}{2}=-\frac{x^{2}}{2}+c\Rightarrow \frac{x^{2}} {2}+\frac{y^{2}}{2}=c\)
\(\Rightarrow {x^{2}}+{y^{2}}=C \)
For \(x=1,y=0\Rightarrow c=1\), Hence \(x^{2}+y^{2}=1\)
Question
Consider the differential equation \(\frac{\mathrm{d} y}{\mathrm{d} x}=-\frac{x}{y}\), with y(1) = 2 .
(a) Solve the equation
(i) as a D.E of separable variables
(ii) as a homogeneous D.E.
(iii) as a linear D.E. of first order (using integrating factor)
(b) Find the actual value of \(y\)(2).
(c) Use Euler’s method to find an approximation for \(y\)(2)
(i) by using a step of \(h\) = 0.2 and completing a table of three columns \((n,\ x_{n} ,\ y_{n})\);
(ii) by using a step of \(h\) = 0.01 (give directly the approximation of y(2))
▶️Answer/Explanation
Ans
(a) the solution (by any method is \(y=\frac{C}{x}\) where \(C\) is a constant.
(ⅰ) \(\frac{\mathrm{d} y}{\mathrm{d} x}=-\frac{y}{x}\Rightarrow \frac{\mathrm{d} y}{\mathrm{y}}=-\frac{\mathrm{d} x}{\mathrm{x}}\Rightarrow \int \frac{\mathrm{d} y}{\mathrm{y}} =-\int \frac{\mathrm{d} x}{\mathrm{x}}\Rightarrow \ln y =-\ln x+c\Rightarrow \ln yx=c\Rightarrow yx=e^{e}\)
\(y=\frac{e^{e}}{x}=\frac{C}{x}\)
(ii) Let \(u=\frac{y}{x}\Rightarrow y=xu\Rightarrow \frac{\mathrm{d} y}=u+x\frac{\mathrm{d} u}{\mathrm{d} x}\)
\(u+x\frac{\mathrm{d} u}{\mathrm{d} x}=-u\Rightarrow x\frac{\mathrm{d} u}{\mathrm{d} x}=-2u\Rightarrow \frac{\mathrm{d} u}{\mathrm{u}}=-2\frac{\mathrm{d} }{\mathrm{d}x}\Rightarrow \int \frac{\mathrm{d} u}{\mathrm{u}}=-2\frac{\mathrm{d} }{\mathrm{d} x}\Rightarrow \ln u=-2\ln x+c\)
\(\Rightarrow \ln ux^{2}=c\Rightarrow ux^{2}=e^{c}\Rightarrow \frac{y}{x}=e^{c}\Rightarrow \frac{y}{x}=e^{c}\Rightarrow y=\frac{C}{x}\)
(iii) \(\frac{\mathrm{d} y}{\mathrm{d} x}+\frac{y}{x}=0,\ P(x)=\frac{1}{x}, \ Q(x)=0\), Integrating factor \( I=e^{\int P(x)dx}=e^{\int \frac{1}{x}dx}=e^{\ln x}=x\)
\(Iy=\int IQdx\Rightarrow xy=\int 0dx\Rightarrow xy=c\Rightarrow y=\frac{c}{x}\)
For \(x=1, y=2\Rightarrow C=2\). Hence \(y=\frac{2}{x}\)
(b) For \(x\)=2, \(y\)=1
(c) (i) \(x_{n+1}=x_{n}+0.2\), \(y_{n+1}=y_{n}-0.2\frac{y_{n}}{x_{n}}\)
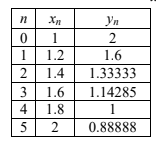
(ii) \(x_{n+1}=x_{n}+0.01, y_{n+1}=y_{n}-0.01\frac{y_{n}}{x_{n}}\ (100steps)\ y\cong 0.99497…\cong 0.995\)
Question
Given that \(\frac{\mathrm{d} y}{\mathrm{d} x}=e^{x}-2x\) and \(y\) = 3 when \(x\) = 0, find an expression for \(y\) in terms of \(x\).
▶️Answer/Explanation
Ans
\(y=e^{x}-x^{2}+C\)
\(3=e^{0}-0+C\Rightarrow C=2\)
\(y=e^{x}-x^{2}+2\)
Question
Solve the differential equation \(\frac{\mathrm{d} y}{\mathrm{d} x}=2xy^{2}\) given that \(y\) = 1 when \(x\) = 0 . Give your answer in the form \(y= f (x)\).
▶️Answer/Explanation
Ans
Separating variables
\(\int \frac{\mathrm{d} y}{\mathrm{y^{2}}}=\int 2x\ dx\)
\(-\frac{1}{y}=x^{2}+C\)
Using \(y(0)=1\) gives \(C=-1\left ( -\frac{1}{y}=x^{2}-1 \right )\)
\(y=-\frac{1}{x^{2}-1}\left ( =\frac{1}{1-x^{2}} \right )\)
Question
Solve the differential equation \(\frac{\mathrm{d} y}{\mathrm{d} x}=2xy^{2}\) given that \(y\) = 1 when \(x\) = 0 . Give your answer in the form \(y= f (x)\).
▶️Answer/Explanation
Ans
Separating variables
\(\int \frac{\mathrm{d} y}{\mathrm{y^{2}}}=\int 2x\ dx\)
\(-\frac{1}{y}=x^{2}+C\)
Using \(y(0)=1\) gives \(C=-1\left ( -\frac{1}{y}=x^{2}-1 \right )\)
\(y=-\frac{1}{x^{2}-1}\left ( =\frac{1}{1-x^{2}} \right )\)
Question
Solve the differential equation \(x\frac{\mathrm{d} y}{\mathrm{d} x}-y^{2}=1\) given that \(y\) = 0 when \(x\) = 2. Give your answer in the form \(y = f(x)\).
▶️Answer/Explanation
Ans
\(x\frac{\mathrm{d} y}{\mathrm{d} x}-y^{2}=1,\Rightarrow x\frac{\mathrm{d} y}{\mathrm{d} x}=y^{2}+1\)
\(\frac{dy}{y^{2}+1}=\frac{dx}{x}\)
\(arctan\ y=\ln x+c\)
\(y=0,x=2\Rightarrow arctan\ 0=\ln 2+c\Rightarrow -\ln 2=c\)
\(arctan\ y=\ln x-\ln 2=\ln \frac{x}{2}\)
\(y=\tan \left ( \ln \frac{x}{2} \right )\)
Question
Solve the differential equation \(xy\frac{\mathrm{d} y}{\mathrm{d} x}=1+y^{2}\) , given that \(y\) = 0 when \(x\) = 2.
▶️Answer/Explanation
Ans
\(x\frac{\mathrm{d} y}{\mathrm{d} x}=1+y^{2}\Rightarrow \int \frac{y}{1+y}dx=\int \frac{1}{x}dx\)
\(\frac{1}{2}\ln (1+y^{2})=\ln x+\ln c\)
\(1+y^{2}=kx^{2}(k=c^{2})\)
\(y=0\) when \(x=2\), and so \(1=4k\)
Thus, \(1+y^{2}=\frac{1}{4}x^{2}\) or \(x^{2}-4y^{2}=4\).
Question
Find the general solution of the differential equation \(\frac{\mathrm{d} x}{\mathrm{d} t}=kx(5-x)\) where 0 < x < 5 , and \(k\) is a constant.
HINT: Show first that \(\frac{1}{x(5-x)}=\frac{1}{5}\left ( \frac{1}{x}+\frac{1}{5-x} \right )\)
▶️Answer/Explanation
Ans
Given \(\frac{\mathrm{d} x}{\mathrm{d} t}=kx(5-x)\)
then \(\frac{1}{x(5-x)}\frac{\mathrm{d} x}{\mathrm{d} t}=k\)
\(\int \frac{1}{5x}+\frac{1}{5(5-x)}dx=\int kdt\)
\(\frac{1}{5}\ln x-\frac{1}{5}\ln(5-x)=kt\) or \(\left ( \frac{x}{5-x} \right )^{\frac{1}{5}}=Ae^{kt}\) or \(\left ( \frac{x}{5-x} \right )=Ae^{5kt}\)
Question
Solve the differential equation \(\left ( x^{2}+1 \right )\frac{\mathrm{d} y}{\mathrm{d} x}-xy=0\) where \(x\) =0, \(y\) = 0 , given that \(y\) = 1 when \(x\)=1.
▶️Answer/Explanation
Ans
\(\frac{\mathrm{d} y}{\mathrm{y}}=\frac{xdx}{x^{2}+1}\)
\(\int \frac{\mathrm{d} y}{\mathrm{y}}=\ln y\)
\(\int \frac{x}{x^{2}+1}dx=\frac{1}{2}\ln (x^{2}+1)\)
EITHER
\(\ln y=\frac{1}{2}\ln(x^{2}+1)+\ln C\)
\(\ln y=\ln C\sqrt{x^{2}+1}\)
\(1=C\sqrt{2}\) for substituting \(x=1,y=1\)
\(C=\frac{1}{\sqrt{2}}\)
\(y=\sqrt{\frac{x^{2}+1}{2}}\)
OR
\(\ln y=\frac{1}{2}\ln (x^{2}+1)+A\)
\(\ln 1=\frac{1}{2}\ln 2+A\) for substituting \(x=1,y=1\)
\(A=-\frac{1}{2}\ln) 2\)
\(\ln y=\frac{1}{2}\ln (x^{2}+1)-\frac{1}{2}\ln 2\left ( \frac{1}{2}\ln (x^{2}+1)-0.347 \right )\)
\(\left ( \ln y=\ln \sqrt{\frac{x^{2}+1}{2}} \right )\)
\(\left ( y=\sqrt{\frac{x^{2}+1}{2}} \right )\)
Question
Solve the differential equation \(\left ( x^{2}+1 \right )\frac{\mathrm{d} y}{\mathrm{d} x}-xy=0\) where \(x\) =0, \(y\) = 0 , given that \(y\) = 1 when \(x\)=1.
▶️Answer/Explanation
Ans
\(\frac{\mathrm{d} y}{\mathrm{y}}=\frac{xdx}{x^{2}+1}\)
\(\int \frac{\mathrm{d} y}{\mathrm{y}}=\ln y\)
\(\int \frac{x}{x^{2}+1}dx=\frac{1}{2}\ln (x^{2}+1)\)
EITHER
\(\ln y=\frac{1}{2}\ln(x^{2}+1)+\ln C\)
\(\ln y=\ln C\sqrt{x^{2}+1}\)
\(1=C\sqrt{2}\) for substituting \(x=1,y=1\)
\(C=\frac{1}{\sqrt{2}}\)
\(y=\sqrt{\frac{x^{2}+1}{2}}\)
OR
\(\ln y=\frac{1}{2}\ln (x^{2}+1)+A\)
\(\ln 1=\frac{1}{2}\ln 2+A\) for substituting \(x=1,y=1\)
\(A=-\frac{1}{2}\ln) 2\)
\(\ln y=\frac{1}{2}\ln (x^{2}+1)-\frac{1}{2}\ln 2\left ( \frac{1}{2}\ln (x^{2}+1)-0.347 \right )\)
\(\left ( \ln y=\ln \sqrt{\frac{x^{2}+1}{2}} \right )\)
\(\left ( y=\sqrt{\frac{x^{2}+1}{2}} \right )\)
Question
Solve the differential equation \(\left ( x+2 \right )^{2}\frac{\mathrm{d} y}{\mathrm{d} x}=4xy\), given that \(y\) = 1 when \(x\) =-1.
▶️Answer/Explanation
Ans
\(\int \frac{1}{y}dy=\int \frac{4x}{(x+2)^{2}}dx\)
Let \(u=x+2\ \Rightarrow \ x=u-2\)
\(du=dx\)
\(\ln y=\int \frac{4(u-2)}{u^{2}} du\)
\(=\int \frac{4}{u}-\frac{8}{u^{2}}du\)
\(\ln y=4\ln u+8u^{-1}+c\)
\(\ln y=4\ln (x+2)+\frac{8}{x+2}+c\)
\((-1,1)\Rightarrow c=-8\)
\(\Rightarrow \ln y=4 \ln(x+2)+\frac{8}{x+2}-8\)
Question
Solve the differential equation \(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{1+y^{2}}{1+x^{2}}\),given that \(y=\sqrt{3}\) when \(x=\frac{\sqrt{3}}{3}\). Give your answer in the form
\(y=\frac{ax+\sqrt{a}}{a-x\sqrt{a}}\) where \(a\ \epsilon \ Z^{+}\).
▶️Answer/Explanation
Ans
\(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{1+y^{2}}{1+x^{2}}\)
\(\Rightarrow \int \frac{1}{1+y^{2}}dy=\int \frac{1}{x^{2}}dx\)
\(\Rightarrow arctan\ y=arctan\ x+k\)
\(\Rightarrow arctan \sqrt{3}=arctan \frac{\sqrt{3}}{3}+k\)
\(\Rightarrow \frac{\pi }{3}=\frac{\pi }{6}+k\Rightarrow k=\frac{\pi }{6}\)
\(\Rightarrow arctan\ y=arctan\ x+\frac{\pi }{6}\)
\(\Rightarrow y=\tan \left (arctan\ x+\frac{\pi }{6} \right )\)
\(\Rightarrow y=\frac{x+\tan \frac{\pi }{6}}{1-x\tan \frac{\pi }{6}}\)
\(\Rightarrow y=\frac{x+\frac{\sqrt{3}}{3}}{1-x\frac{\sqrt{3}}{3}}\)
\(\Rightarrow y=\frac{3x+\sqrt{3}}{3-x\sqrt{3}}\)
Question
The equation of motion of a particle with mass m, subjected to a force \(kx\) can be written as \(kx=mv\frac{\mathrm{d} v}{\mathrm{d} x}\), where \(x\) is the displacement and \(v\) is the velocity. When \(x\) = 0, \(v=v_{0}\).
Find \(v\), in terms of \(m\), \(k\) and \(v_{0}\).
▶️Answer/Explanation
Ans
If \(kx=mv\frac{\mathrm{d} v}{\mathrm{d} x}\) Then \(\int kx\ dx=\int mv\ dv\) (using separation of variables)
\(\Rightarrow \frac{1}{2}kx^{2}=\frac{1}{2}mv^{2}+C\)
When \(x=0,v=v_{0}\), therefore \(C=-\frac{1}{2}mv_{0}^{2}\) Therefore \(v^{2}=v_{0}^{2}+\frac{kx^{2}}{m}\)
Therefore when \(x=2,v=\sqrt{v_{0}^{2}+\frac{4k}{m}}\)
Question
A sample of radioactive material decays at a rate which is proportional to the amount of material present in the sample. Find the half-life of the material if 50 grams decay to 48 grams in 10
years.
▶️Answer/Explanation
Ans
If \(A\) g is present at any time, then \(\frac{\mathrm{d} A}{\mathrm{d} t}=ka\) where \(k\) is a constant.
Then, \(\int \frac{\mathrm{d} A}{\mathrm{A}}=k\int dt\)
\(\Rightarrow \ln A=kt+C\)
\(\Rightarrow A=e^{kt+c}=c_{1}e^{kt}\)
When \(t=0,c_{1}=50\Rightarrow 48=50e^{10k}\)
\(\frac{\ln 0.96}{10}=k\) or \(k=-0.00408(2)\)
For half life, \(25=50e^{kt}\Rightarrow \ln 0.5=kt\Rightarrow t=\frac{10\ln 0.5}{\ln 0.96}=169.8\).
Therefore, half-life \(= 170years(3\ s.f.)\)
Question
The tangent to the curve \(y = f(x)\) at the point \(P(x, y)\) meets the \(x\)-axis at Q (\(x\) – 1, 0). The curve meets the \(y\)-axis at R(0, 2). Find the equation of the curve.
▶️Answer/Explanation
Ans
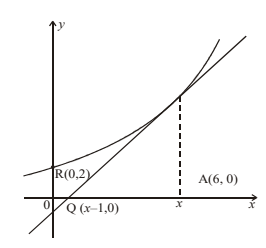
From the diagram,
\(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{y}{1}\Rightarrow \frac{\mathrm{d} y}{\mathrm{y}}=\int dx\Rightarrow \ln y+x+c\Rightarrow y=e^{x+c}=Ae^{x}\).
But R (0,2) lies on the curve and so \(A = 2\).
\(y=2e^{x}\)
Question
When air is released from an inflated balloon it is found that the rate of decrease of the volume of the balloon is proportional to the volume of the balloon. This can be represented by the
differential equation \(\frac{\mathrm{d} v}{\mathrm{d} t}=-kv\), where v is the volume, t is the time and k is the constant of proportionality.
(a) If the initial volume of the balloon is \(v_{0}\), find an expression, in terms of \(k\), for the volume of the balloon at time \(t\).
(b) Find an expression, in terms of \(k\), for the time when the volume is \(\frac{v_{0}}{2}\).
▶️Answer/Explanation
Ans
(a) \(Given\frac{\mathrm{d} v}{\mathrm{d} t}=-kv\Leftrightarrow \int \frac{\mathrm{d} v}{\mathrm{v}}=-k\int dt\)
\(\Leftrightarrow \ln v=-kt+C\)
\(\Leftrightarrow v=Ae^{-kt}(A=e^{C})\)
At \(t=0,v=v_{0}\Rightarrow A=v_{0}\Leftrightarrow v=v_{0}e^{-kt}\)
(b) Put \(v=\frac{v_{0}}{2} then \frac{v_{0}}{2}=v_{0}e^{-kt}\)
\(\Leftrightarrow \frac{1}{2}=e^{-kt}\Leftrightarrow \ln \frac{1}{2}=-kt\)
\(\Leftrightarrow t=\frac{\ln 2}{k}\)
Question
Show that the solution of the homogeneous differential equation
\(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{y}{x}+1,x> 0,\)
given that \(y\) = 0 when \(x = e\), is \(y = x(\ln x – 1)\).
▶️Answer/Explanation
Ans
(a) use the substitution \(y = vx\)
\(\frac{\mathrm{d} v}{\mathrm{d} x}x+v=v+1\)
\(\int dv=\int \frac{\mathrm{d} x}{\mathrm{x}}\)
by integration
\(v=\frac{y}{x}=\ln x+c\)
OR
the equation can be rearranged as first order linear …
Question
Solve the differential equation
\(x^{2}\frac{\mathrm{d} y}{\mathrm{d} x}=y^{2}+3xy+2x^{2}\)
given that \(y\) = –1 when \(x \)= 1. Give your answer in the form \(y = f(x)\).
▶️Answer/Explanation
Ans
put \(y=vx\) so that \(=\frac{\mathrm{d} y}{\mathrm{d} x}=v+x\frac{\mathrm{d} v}{\mathrm{d} x}\)
\(v+x\frac{\mathrm{d} v}{\mathrm{d} x}=\frac{v^{2}x^{2}+3vx^{2}+2x^{2}}{x^{2}}=(v^{2}+3v+2)\)
\(x\frac{\mathrm{d} v}{\mathrm{d} x}=v^{2}+2v+2\)
\(\int \frac{dv}{v^{2}+2v+2}=\int \frac{dx}{x}\)
\(\int \frac{dv}{(v+1)^{2}+1}=\int \frac{dx}{x}\)
\(arctan(v+1=\ln x+c\)
\(arctan(\frac{y}{x}+1)=\ln x+c\)
When \(x=1,y=-1\), so \(c=0\)
\(\frac{y}{x}+1=\tan \ln x\)
\(y=x(\tan \ln x-1)\)
Question
Consider the differential equation \(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{y^{2}+x^{2}}{2x^{2}}\) for which \(y\) = –1 when \(x\) = 1.
(i) Solve the differential equation giving your answer in the form \(y = f(x)\).
(ii) Find the value of \(y\) when \(x \)= 2.
▶️Answer/Explanation
Ans
(i) let \(y=vx\ \Rightarrow \frac{\mathrm{d} y}{\mathrm{d} x}=v+x\frac{\mathrm{d} v}{\mathrm{d} x}\)
\(v+x\frac{\mathrm{d} v}{\mathrm{d} x}=\frac{v^{2}x^{2}+x^{2}}{2x^{2}}\Rightarrow x\frac{\mathrm{d} v}{\mathrm{d} x}=\frac{1-2v+v^{2}}{2}\Rightarrow x\frac{\mathrm{d} v}{\mathrm{d} x}=\frac{(1-v^{2})}{2}\)
\(\Rightarrow \int \frac{2}{(1-v^{2})}dv=\int \frac{1}{x}dx \int 2(1-v)^{-1}=\ln x+c\)
\(\Rightarrow \frac{2}{1-\frac{y}{x}}=\ln x+c\)
when \(x=1,y=-1\Rightarrow c=1\)
\(\Rightarrow \frac{2x}{x-y}=\ln x+1\Rightarrow y=x-\frac{2x}{1+\ln x}\left ( =\frac{x\ln x-x}{1+\ln x} \right )\)
(ii) when \(x=2,y=-0.362\left ( accept\ 2 -\frac{4}{1+\ln 2}\right )\)
Question
Solve the differential equation
\(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{y}{x}+\frac{y^{2}}{x^{2}}\) (where \(x\) > 0)
given that \(y\) = 2 when \(x\) = 1. Give your answer in the form \(y = f(x)\).
▶️Answer/Explanation
Ans
put \(y=vx so that \frac{\mathrm{d} y}{\mathrm{d} x}=v+x\frac{\mathrm{d} v}{\mathrm{d} x}\)
the equation becomes \(v+x\frac{\mathrm{d} v}{\mathrm{d} x}=v+v^{2}\Rightarrow x\frac{\mathrm{d} v}{\mathrm{d} x}=v^{2}\)
separating variables, \(\int \frac{\mathrm{d} x}{\mathrm{x}}=\int \frac{\mathrm{d} v}{\mathrm{v^{2}}}\)
\(\Rightarrow \ln x=-v^{-1}+C\)
substituting for v, \(\ln x=-\frac{x}{y}+C\)
substituting the boundary conditions,
\(0=-\frac{1}{2}+C\) \(C=\frac{1}{2}\)
the solution is \(\ln x=-\frac{x}{y}+\frac{1}{2}\)
\(\Rightarrow to\ y=\frac{2x}{1-2\ln x}\)
Question
The variables x and y are related by \(\frac{\mathrm{d} y}{\mathrm{d} x}=y\tan x=\cos x\).
Solve the differential equation given that \(y = 0\) when \(x = π\). Give the solution in the form \(y = f(x)\).
▶️Answer/Explanation
Ans
integrating factor is \(e^{\int -\tan xdx}=e^{\ln cosx}=\cos x\)
\(\Rightarrow y\cos x=\frac{1}{2}\int (1+\cos 2x)dx\)
\(\Rightarrow y\cos x=\frac{x}{2}+\frac{\sin 2x}{4}+k\)
when \(x=\pi, y=0\Rightarrow k=-\frac{\pi }{2}\)
\(\Rightarrow y\cos x=\frac{x}{2}+\frac{\sin 2x}{4}-\frac{\pi }{2}\)
\(\Rightarrow y\sec\left ( \frac{x}{2}+\frac{\sin 2x}{4}-\frac{\pi}{2} \right )\)
Question
Find the solution to the differential equation
\((\cos x-\sin x)\frac{\mathrm{d} y}{\mathrm{d} x}+(\cos x+\sin x)y=\cos x+\sin x\)
given that y = –1 when \(x=\frac{\pi }{2}\).
▶️Answer/Explanation
Ans
\((\cos x-\sin x)\frac{\mathrm{d} y}{\mathrm{d} x}+(\cos x+\sin x)y=(\cos x+\sin x)\)
\(\frac{\mathrm{d} y}{\mathrm{d} x}+\frac{\cos x+\sin x}{\cos x-\sin x}y=\frac{\cos x+\sin x}{\cos x-\sin x}\)
IF \(=e^{\int \frac{\cos x+\sin x}{\cos x-\sin x}dx}=e^{-\ln (\cos x-\sin x)}=\frac{1}{\cos x-\sin x}\)
\(\frac{y}{\cos x-\sin x}=\int \frac{\cos x+\sin x}{(\cos x-\sin x)^{2}}dx=\frac{1}{\cos x-\sin x}+k\)
Hence \(y=1+k(\cos x-\sin x)\)
\(x=\frac{\pi }{2},y=-1\Rightarrow -1=1+k(-1)\Rightarrow k=2\)
\(y=1+2(\cos x-\sin x)\)
Note: It is acceptable to solve the equation using separation of variables.
Question
Given that \(\frac{\mathrm{d} y}{\mathrm{d} x}+2y\tan x=\sin x\), and \(y\) = 0 when \(x=\frac{\pi }{3}\), find the maximum value of \(y\).
▶️Answer/Explanation
Ans
integrating factor \(=e^{\int 2tanxdx}=e^{2\ln \sec x}=\sec^{2}x\)
\(y\sec^{2}x=\int \sin x \sec^{2}x\ dx=\int \sec x\tan x\ dx=\sec x+C\)
substituting, \(0=2+C so C=-2\)
the solution is \(y=\cos x-2\cos^{2}x\)
EITHER
using a GDC, maximum value of y is 0.125
OR
\(y’=-\sin x+4\sin x\cos x=0\)
\(\Rightarrow \cos x=\frac{1}{4}\)
\(\Rightarrow y=\frac{1}{8}\)
Question
Solve the differential equation \(\left ( u+3v^{3} \right )\frac{\mathrm{d} v}{\mathrm{d} u}=2v\), giving your answer in the form \(u = f(v)\).
▶️Answer/Explanation
Ans
\((u+3v^{3})\frac{\mathrm{d} v}{\mathrm{d} u}=2v\)
\(\frac{\mathrm{d} u}{\mathrm{d} v}=\frac{(u+3v^{3})}{2v}=\frac{u}{2v}+\frac{3v^{2}}{2}\)
\(\frac{\mathrm{d} u}{\mathrm{d} v}-\frac{u}{2v}=\frac{3v^{2}}{2}\)
IF is \(\int e^{-\frac{1}{2v}dv}=e^{-\frac{1}{2}\ln v}=v^{-\frac{1}{2}}\)
\(\frac{u}{\sqrt{v}}=\int \frac{3v\frac{3}{2}}{2}dv=\fAnsrac{3}{5}v^{\frac{5}{2}}+c\)
\(u=\frac{3}{5}v^{3}+c\sqrt{v}\)
Question
Consider the differential equation
\(x\frac{\mathrm{d} y}{\mathrm{d} x}-2y=\frac{x^{3}}{x^{2}+1}\).
(a) Find an integrating factor for this differential equation.
(b) Solve the differential equation given that \(y =1\) when \(x =1\), giving your answer in the form \(y = f (x)\).
▶️Answer/Explanation
Ans
(a) Rewrite the equation in the form \(\frac{\mathrm{d} y}{\mathrm{d} x}-\frac{2}{x}y=\frac{x^{2}}{x^{2}+1}\)
Integrating factor \(e^{\int \frac{2}{x}dx}=2^{-2\ln x}=\frac{1}{x^{2}}\)
(b) [in fact we multiply by IF: \(\frac{1}{x^{2}}\frac{\mathrm{d} y}{\mathrm{d} x}-\frac{2}{x^{3}}y=\frac{1}{x^{2}+1}\frac{\mathrm{d} }{\mathrm{d} x}\left ( \frac{y}{x^{2}} \right )=\frac{1}{x^{2}+1}]\)
\(\frac{y}{x^{2}}=\int \frac{dx}{x^{2}+1}=arctan\ x+C\)
Substitute \(x=1,y=1\).
\(1=\frac{\pi }{4}+C\Rightarrow C=1-\frac{\pi }{4}\)
\(y=x^{2}\left ( arctan\ x+1-\frac{\pi }{4} \right )\)
Question
A curve that passes through the point (1, 2) is defined by the differential equation
\(\frac{\mathrm{d} y}{\mathrm{d} x}=2x\left ( 1+x^{2} -y\right )\)
Solve the differential equation giving your answer in the form \(y = f (x)\).
▶️Answer/Explanation
Ans
\(\frac{\mathrm{d} y}{\mathrm{d} x}=2x(1+x^{2}-y)\)
\(\frac{\mathrm{d} y}{\mathrm{d} x}=2xy=2x(1+x^{2})\)
Integrating factor is \(e^{\int 2xdx}=e^{x^{2}}\)
So, \(e^{x^{2}}y=\int \left ( 2xe^{x^{2}}+2xe^{x^{2}}x^{2} \right )dx=e^{x^{2}}+x^{2}e^{x^{2}}-\int 2xe^{x^{2}}dx\)
\(=e^{x^{2}}+x^{2}e^{x^{2}}-e^{x^{2}}+k\)
\(=x^{2}e^{x^{2}}+k\)
\(y=x^{2}+ke^{-x^{2}}\)
\(x=1,y=2\rightarrow 2=1+ke^{-1}\)
\(k=e\)
\(y=x^{2}+e^{1-x^{2}}\)
Question
A curve that passes through the point (1, 2) is defined by the differential equation
\(\frac{\mathrm{d} y}{\mathrm{d} x}=2x\left ( 1+x^{2} -y\right )\)
Solve the differential equation giving your answer in the form \(y = f (x)\).
▶️Answer/Explanation
Ans
\(\frac{\mathrm{d} y}{\mathrm{d} x}=2x(1+x^{2}-y)\)
\(\frac{\mathrm{d} y}{\mathrm{d} x}=2xy=2x(1+x^{2})\)
Integrating factor is \(e^{\int 2xdx}=e^{x^{2}}\)
So, \(e^{x^{2}}y=\int \left ( 2xe^{x^{2}}+2xe^{x^{2}}x^{2} \right )dx=e^{x^{2}}+x^{2}e^{x^{2}}-\int 2xe^{x^{2}}dx\)
\(=e^{x^{2}}+x^{2}e^{x^{2}}-e^{x^{2}}+k\)
\(=x^{2}e^{x^{2}}+k\)
\(y=x^{2}+ke^{-x^{2}}\)
\(x=1,y=2\rightarrow 2=1+ke^{-1}\)
\(k=e\)
\(y=x^{2}+e^{1-x^{2}}\)
Question
A curve that passes through the point (1, 2) is defined by the differential equation
\(\frac{\mathrm{d} y}{\mathrm{d} x}=2x\left ( 1+x^{2} -y\right )\)
Solve the differential equation giving your answer in the form \(y = f (x)\).
▶️Answer/Explanation
Ans
\(\frac{\mathrm{d} y}{\mathrm{d} x}=2x(1+x^{2}-y)\)
\(\frac{\mathrm{d} y}{\mathrm{d} x}=2xy=2x(1+x^{2})\)
Integrating factor is \(e^{\int 2xdx}=e^{x^{2}}\)
So, \(e^{x^{2}}y=\int \left ( 2xe^{x^{2}}+2xe^{x^{2}}x^{2} \right )dx=e^{x^{2}}+x^{2}e^{x^{2}}-\int 2xe^{x^{2}}dx\)
\(=e^{x^{2}}+x^{2}e^{x^{2}}-e^{x^{2}}+k\)
\(=x^{2}e^{x^{2}}+k\)
\(y=x^{2}+ke^{-x^{2}}\)
\(x=1,y=2\rightarrow 2=1+ke^{-1}\)
\(k=e\)
\(y=x^{2}+e^{1-x^{2}}\)
Question
Solve the following differential equation
\(\left ( x+1 \right )\left ( x+2 \right )\frac{\mathrm{d} y}{\mathrm{d} x}+y=x+1\)
giving your answer in the form \(y = f (x)\).
HINT: Show first that \(\frac{1}{\left ( x+1 \right )\left ( x+2 \right )}=\frac{1}{x+1}-\frac{1}{x+2}\)
▶️Answer/Explanation
Ans
Rewrite the equation in the form
\(\frac{\mathrm{d} y}{\mathrm{d} x}+\frac{y}{(x+1)(x+2)}=\frac{1}{x+2}\)
\(I=exp\left ( \int \frac{dx}{(x+1)(x+2)} \right )=exp\left (\int \left ( \frac{1}{x+1}-\frac{1}{x+2} \right )dx \right )=exp\ln \left ( \frac{x+1}{x+2} \right )=\frac{x+1}{x+2}\)
Hence,
\(\left ( \frac{x+1}{x+2} \right )y=\ln (x+2)+\frac{1}{x+2}+C\)
\(y=\left ( \frac{x+2}{x+1} \right )\left \{ (x+2)+\frac{1}{x+2} +C\right \}\)
Question
Consider the differential equation \(\frac{\mathrm{d} y}{\mathrm{d} y}+\frac{xy}{4-x^{2}}=1\), where \(\left | x \right |<2\) and \(y = 1\) when \(x = 0\).
(i) By first finding an integrating factor, solve this differential equation. Give your answer in the form \(y = f(x)\).
(ii) Calculate, correct to two decimal places, the value of \(y\) when \(x = 1\).
▶️Answer/Explanation
Ans
(i) Integrating factor \(=e\int \left ( \frac{x}{4-x^{2}} \right )dx=e\left ( -\frac{1}{2}\ln (4-x^{2}) \right )=\frac{1}{\sqrt{4-x^{2}}}\)
\(\frac{y}{{\sqrt{4-x^{2}}}}=arcsin\left ( \frac{x}{2} \right )+C\)
Putting \(x=0,y=1,\Rightarrow \frac{1}{2}=C\)
Therefore, \(y={\sqrt{4-x^{2}}}\left ( arcsin\left ( \frac{x}{2} \right ) +\frac{1}{2}\right )\)
Question
Consider the differential equation \(\frac{\mathrm{d} y}{\mathrm{d} x}=x^{2}+y^{2}\) where \(y\) = 1 when \(x\) = 0.
(a) Use Euler’s method with step length 0.1 to find an approximate value of \(y\) when \(x\) = 0.4.
(b) Write down, giving a reason, whether your approximate value for \(y\) is greater than or less than the actual value of \(y\).
▶️Answer/Explanation
Ans
(a) \(x_{n+1}=x_{n}+0.1\), \(y_{n+1}=y_{n}+0.1(x_{n}^{2}+y_{n}^{2})\)
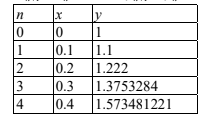
approximate value of \(y=1.57\)
(b) the approximate value is less than the actual value because it is assumed that \(\frac{\mathrm{d} y}{\mathrm{d} x}\) remains constant throughout each interval whereas it is actually an increasing function.
Question
Given that \(\frac{\mathrm{d} y}{\mathrm{d} x}-2y^{2}=e^{x}\) and \(y\) = 1 when \(x\) = 0, use Euler’s method with a step length of 0.1 to find an approximation for the value of \(y\) when \(x\) = 0.4. Give all intermediate values with maximum possible. accuracy.
▶️Answer/Explanation
Ans
\( x_{n+1}=x_{n}+0.1\), \(y_{n+1}=y_{n}+0.1(e^{x_{n}}+2y_{n}^{2})\)
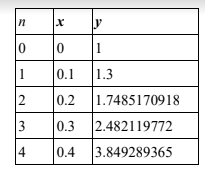
required approximation = 3.85
Question
Consider the differential equation \(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{y^{2}+x^{2}}{2x^{2}}\) for which y = –1 when x = 1. Use Euler’s method with a step length of 0.25 to find an estimate for the value of y when x = 2.
Notice: we have seen this equation as a homogeneous DE.
▶️Answer/Explanation
Ans
\( x_{n+1}=x_{n}+0.25\), \(y_{n+1}=y_{n}+0.25\left ( \frac{y_{n}^{2}+x_{n}^{2}}{2x_{n}^{2}} \right )\)
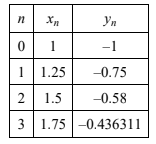
\(\Rightarrow y(2)\approx -0.304\)
Question
A curve that passes through the point (1, 2) is defined by the differential equation
\(\frac{\mathrm{d} y}{\mathrm{d} x}=2x\left ( 1+x^{2}-y \right )\)
(i) Use Euler’s method to get an approximate value of \(y\) when \(x\) = 1.3, taking steps of 0.1. Show intermediate steps to four decimal places in a table.
(ii) How can a more accurate answer be obtained using Euler’s method?
Notice: we have seen this equation as a linear DE.
▶️Answer/Explanation
Ans
(ⅰ) \((x_{n+1}=x_{n}+0.1,y_{n+1}=y_{n}+0.1(2x_{n}(1+x_{n}^{2}-y_{n}))\)
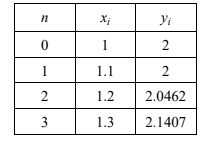
\(f(1.3)=2.14\)
(ii) Decrease the step size.
Question
Consider the differential equation \(\frac{\mathrm{d} y}{\mathrm{d} y}+\frac{xy}{4-x^{2}}=1\), where \(\left | x \right |<1\) and \(y\) = 1 when \(x\) = 0.
(a) Use Euler’s method with \(h = 0.25\), to find an approximate value of \(y\) when \(x\) = 1, giving your answer to two decimal places.
The exact solution of this equation is \(y=\sqrt{4-x^{2}}\left ( arc\sin \left ( \frac{x}{2} \right )+\frac{1}{2} \right )\) and \(y(1)=1.77\)
(b) Sketch the graph of \(y = f(x)\) for 0 ≤ x ≤ 1. Use your sketch to explain why your approximate value of \(y\) is greater than the true value of \(y\).
Notice: we have seen this equation as a linear DE.
▶️Answer/Explanation
Ans
(a) \(x_{n+1}=x_{n}+0.25\), \(y_{n+1}=y_{n}+0.25(1-\frac{x_{n}y_{n}}{4-x_{n}^{2}})\)
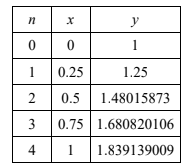
To two decimal places, when \(x = 1, y = 1.84\).
(b) 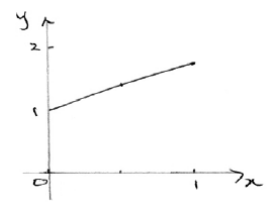
Since the function is concave down the value of \(y\) is over-estimated at each step.
