IB style Practice Questions
9. [Maximum mark: 8]
(a) Write down the first three terms of the binomial expansion of \(\left ( 1+t \right )^{-1}\) in ascending powers of t. [1]
(b) By using the Maclaurin series for \(\cos x\) and the result from part (a), show that the Maclaurin series for \(\sec x\) up to and including the term in \( x^{4}\) \(+\frac{x^{2}}{2}+\frac{5x^{4}}{24} \) [4]
(c) By using the Maclaurin series for \(\arctan x\ ) and the result from part (b), find \(\lim_{x\rightarrow 0}\left ( \frac{\arctan2x}{\sec x-1} \right )\). [3]
▶️Answer/Explanation

Question
Assuming the Maclaurin series for cos x and ln (1 + x) , show that the Maclaurin series for cos (ln (1 + x)) is
\(1-\frac{1}{2}x^2+\frac{1}{2}x^{3}-\frac{5}{12}x^{4}+..\) [4]
By differentiating the series in part (a), show that the Maclaurin series for sin (ln (1 + x))
is x \(-\frac{1}{2}x^2+\frac{1}{6}x^{3}+…\)[4]
Hence determine the Maclaurin series for tan (ln (1 + x)) as far as the term in x3 . [5]
▶️Answer/Explanation
Ans:
(a)
METHOD 1
attempts to substitute ln(1+x)=x – \(\frac{1}{2}x^{2}+\frac{1}{3}x^{4}-\frac{1}{4}x^{4}\)+.. into
cosx = 1 -\(\frac{1}{2}x^{2}+ \frac{1}{24}x^{4}\)….
\(cos(ln(1+x)) =1-\frac{1}{2}(x-\frac{1}{2}x^2+\frac{1}{3}x^3+..)+\frac{1}{24}(x+..)^4+..\)
attempts to expand the RHS up to and including the 4x term
= \(1 -\frac{1}{2}(x^{2}-x^{3}+ \frac{1}{2}x^{4}\)+ \(\frac{2}{3}x^{4}+…)\)
\(= 1-\frac{1}{2}x^{2}+ \frac{1}{2}^{3}-\frac{5}{12}^{4}+…\)
METHOD 2
attempts to substitute \(ln(1+x)\) into cosx= 1-\(\frac{1}{2}x^{2}+ \frac{1}{24}x^{4}\)
\(cos(ln(1+x))= 1-\frac{1}{2}(ln(1+x))^{2}+\frac{1}{24}(ln(1+x))^{4}\)..
attempts to find the Maclaurin series for \((ln(1+x))^2) up to and including the x4 term
\((ln(1+x))^{2}=x^{2}-x^{3}+ \frac{11}{12}x^{4}\)…..
\((ln(1+x))^{2}= x^{4}\) ….
\(= 1-\frac{1}{2}x^{2}+ \frac{1}{2}x^{3}- \frac{5}{12}^{4}\)+….
(b)
\(-sin (ln(1+x))\times \frac{1}{1+x}\)= -x+\(\frac{3}{2}x^{2}-\frac{5}{3}x^{3}+..\)
\(sin (ln(1+x))=-(1+x)(-x+\frac{3}{2}x^{2}-\frac{5}{3}x^{3}+…)\)
attempts to expand the RHS up to and including the \(x^3\) term
\(= x – \frac{3}{2}x^{2}+\frac{5}{3}x^{3}+\frac{-3}{2}x^{3}\)+…\)
\(= x – \frac{1}{2}x^{2}+ \frac{1}{6}x^{3}+…\)
(c)
METHOD 1
let tan (ln(1+x))=a +\(a_{1}+ a_{2}x^{2}+a_{3}x^{3}\)+….
uses \(tan (ln(1+x))= \frac{sin(ln(1+x))}{cos(ln(1+x))}\)to form
\((x-\frac{1}{2}x^{2}+ \frac{1}{6}x^{3}+….)\)\((1-\frac{1}{2}x^{2}+ \frac{1}{2}x^{3}+)^{-1}\)
\((1-\frac{1}{2}x^{2}+ \frac{1}{2}x^{3}+)^{-1}=1+\frac{1}{2}x^2-\frac{1}{2}x^3+..\)
attempts to expand the RHS up to and including the \(x^3\) term
\((x-\frac{1}{2}x^{2}+ \frac{1}{6}x^{3}+….)\)(\(1+\frac{1}{2}x^2-\frac{1}{2}x^3+..\))
\(= x+\frac{1}{2}x^{2}-\frac{1}{2}x^{2}+\frac{1}{6}x^{3}+…\)
\(= x- \frac{1}{2}x^{2}+\frac{2}{3}x^{3}+….\)
METHOD 2
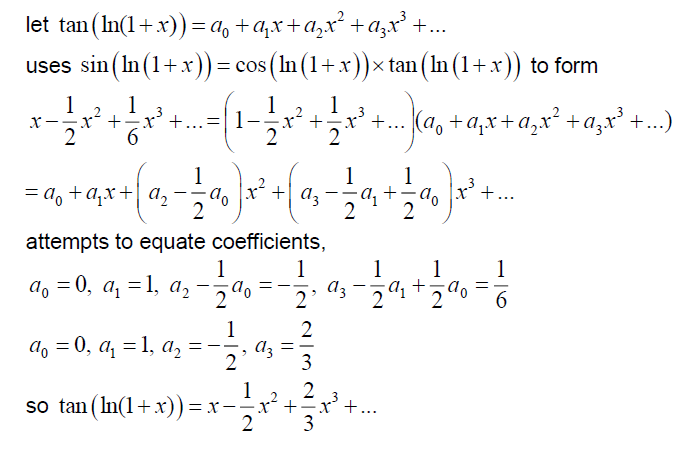
A Maclaurin series is a function that has expansion series that gives the sum of derivatives of that function. The Maclaurin series of a function \(f(x)\) up to order n may be found using Series \([f, {x, 0, n}]\).
It is a special case of Taylor series when x = 0. The Maclaurin series is given by
\[\large f(x)=f(x_{0})+{f}'(x_{0})(x-x_{0})+\frac{{f}”(x_{0})}{2!}(x-x_{0})^{2}+\frac{{f}”'(x_{0})}{3!}(x-x_{0})^{3}+…..\]
The Maclaurin series formula is
\[\large f(x)=\sum_{n=0}^{\infty}\frac{f^{n}(x_{0})}{n!}(x-x_{0})\]
Where,
f(xo), f’(xo), f’‘(xo)……. are the successive differentials when xo = 0.
| Function | Maclaurin Series |
| \(e^{x}\) | \(\sum_{k=0}^{\infty}=1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+…..\) |
| \(sin\;x\) | \(\sum_{k=0}^{\infty}(-1)^{2}=\frac{x^{2k+1}}{(2k+1)!}=x-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}+\frac{x^{7}}{7!}+…..\) |
| \(cos\;x\) | \(\cos x=\sum_{n=0}^{\infty} \frac{(-1)^{n} x^{2 n}}{(2 n) !}=1-\frac{x^{2}}{2 !}+\frac{x^{4}}{4 !}-\frac{x^{6}}{6 !}+\ldots\) |
| \(\frac{1}{1-x}\) | \(\sum_{k=0}^{\infty}x^{k}=1+x+x^{2}+x^{3}+….(if-1<x<1)\) |
| \(ln(1+x)\) | \(\ln (1+x)=\sum_{n=1}^{\infty}(-1)^{n+1} \frac{x^{n}}{n}=x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\cdots\) |
Maclaurin series
Approximating cos(x) with a Maclaurin series (which is like a Taylor polynomial centered at x=0 with infinitely many terms). It turns out that this series is exactly the same as the function itself!
Question
Expanding \(e^{x}\) : Find the Maclaurin Series expansion of \(f(x)=e^{x}\)
▶️Answer/Explanation
Solution:
Recalling that the derivative of the exponential function is \({f}'(x)=e^{x}\) In fact, all the derivatives are \(e^{x}\) .
\({f}'(0)=e^{0}=1\) \({f}”(0)=e^{0}=1\) \({f}”'(0)=e^{0}=1\)
We see that all the derivatives, when evaluated at x = 0, give us the value 1.
Also, f(0)=1, so we can conclude the Maclaurin Series expansion will be simply:
