IBDP Physics 2025 SL&HL: 2.2 Newton’s laws of motion Study Notes

IB DP PhysicsIB DP MathsIB DP ChemistryIB DP Biology

Learning Objectives

  • State Newton’s three laws of motion.
  • Solve translational equilibrium problems using Newton’s 1st Law
  • Identify force pairs using Newton’s 3rd Law
  • Describe forces as interactions between bodies
  • Draw free-body diagrams and analyse them to find the resultant force on a system in one and two dimensions only
  • Understand the nature and use the following contact forces:
    normal, frictional, elastic, viscous drag, buoyancy
  • Understand the nature and use of the following field forces: gravitational, electric, magnetic
  • Define linear momentum and understand that it remains constant unless the system is acted upon by a resultant external force
  • Define Impulse as a resultant external force applied to a system and recall that impulse equals the change in momentum of the system
  • Derive Newton’s 2nd Law from the definition of net force as the rate of change of a momentum of an object, when mass is constant
  • Solve problems using momentum and impulse for collisions and explosion (one dimensional for SL and two dimensional for HL)
  • Understand the scenarios of elastic/inelastic collisions and explosions
  • State that bodies undergoing circular motion travel at a constant speed but still experience acceleration directed radially towards the centre of the circle
  • Draw a vector diagram to illustrate that the acceleration of a particle moving with constant speed in a circle is directed towards the centre of the circle.
  • Recognise the direction of velocity, acceleration and force vectors for an object in circular motion.
  • Understand and solve problems involving centripetal force, centripetal acceleration, period, frequency, angular displacement, linear speed and angular velocity.

Essential Idea:
Classical physics requires a force to change a state of motion, as suggested by Newton in his laws of motion.

Understandings:

  • Objects as point particles
  • Free-body diagrams
  • Translational equilibrium
  • Newton’s laws of motion
  • Solid friction

Applications and Skills:

  • Representing forces as vectors
  • Sketching and interpreting free-body diagrams
  • Describing the consequences of Newton’s first law for translational equilibrium
  • Using Newton’s second law quantitatively and qualitatively
  • Identifying force pairs in the context of Newton’s third law
  • Solving problems involving forces and determining resultant force
  • Describing solid friction (static and dynamic) by coefficients of friction

LAWS OF MOTION

ARISTOTLE’S FALLACY

According to Aristotelian law an external force is required to keep a body in motion. However an external force is required to overcome the frictional forces in case of solids and viscous forces in fluids which are always present in nature.

LINEAR MOMENTUM (P)

Linear momentum of a body is the quantity of motion contained in the body. Momentum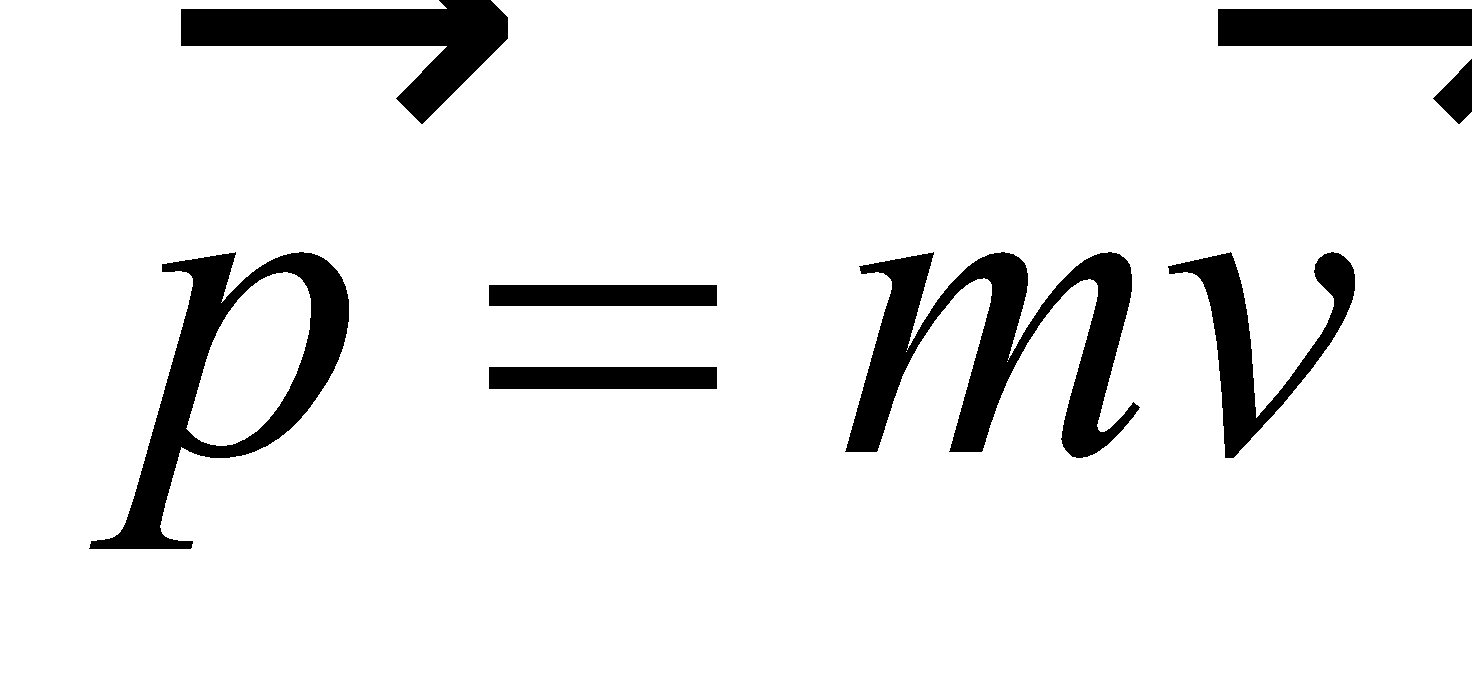  
It is a vector quantity having the same direction as the direction of the velocity. Its SI unit is kg ms–1.

NEWTON’S LAWS OF MOTION

FIRST LAW

A body continues to be in a state of rest or of uniform motion, unless it is acted upon by some external force to change its state.
Newton’s first law gives the qualitative definition of force according to which force is that external cause which tends to change or actually changes the state of rest or motion of a body.
Newton’s first law of motion is the same as law of inertia given by Galileo.
Inertia is the inherent property of all bodies because of which they cannot change their state of rest or of uniform motion unless acted upon by an external force.

SECOND LAW

The rate of change of momentum of a body is directly proportional to the external force applied on it and the change takes place in the direction of force applied.
i.e.,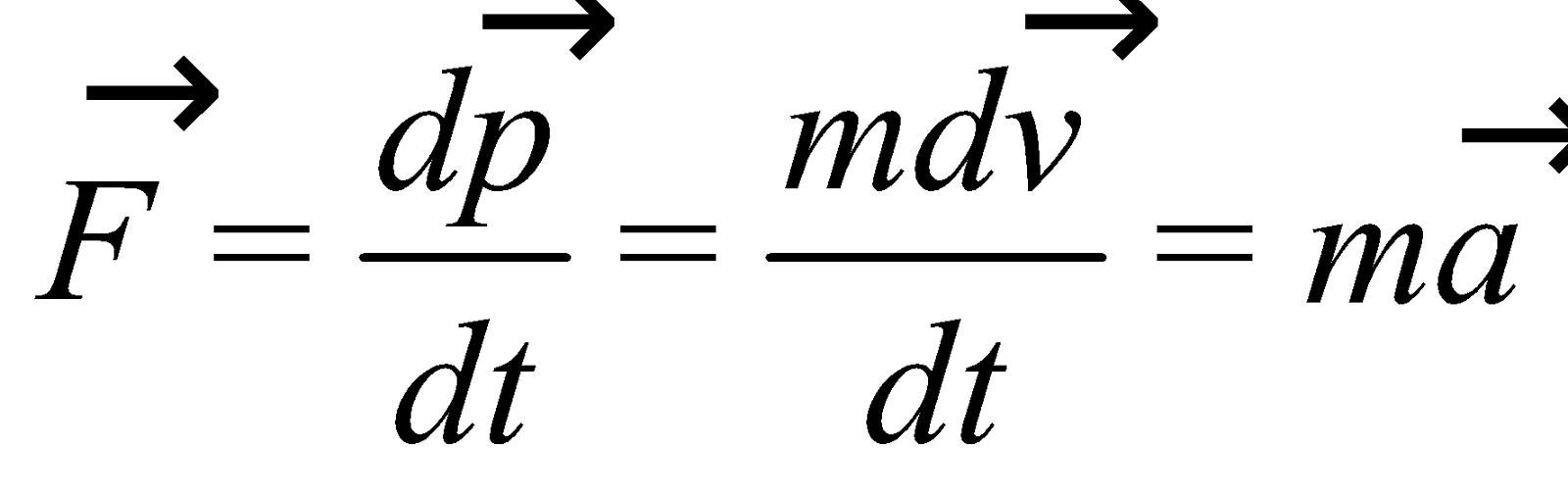   
This is the equation of motion of constant mass system. For variable mass system such as rocket propulsion
And,
The SI unit of force is newton. (One newton force is that much force which produces an acceleration of 1ms–2 in a body of mass 1 kg.
The CGS unit of force is dyne. (1N = 105 dyne)
The gravitational unit of force is kg-wt (kg-f) or g-wt (g-f)
1 kg-wt (kg-f) = 9.8 N, 1 g-wt (g-f) = 980 dyne

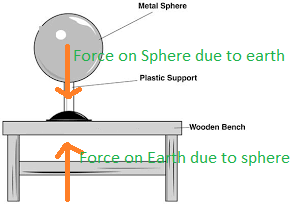
THIRD LAW

To every action there is an equal and opposite reaction. For example – walking , swimming , a horse pulling a cart etc.
Action and reaction act on different bodies and hence cannot balance each other. Action and reaction occur simultaneously. Forces always occur in pairs.

EQUILIBRIUM OF A PARTICLE

A body is said to be in equilibrium when no net force acts on the body.
i.e.,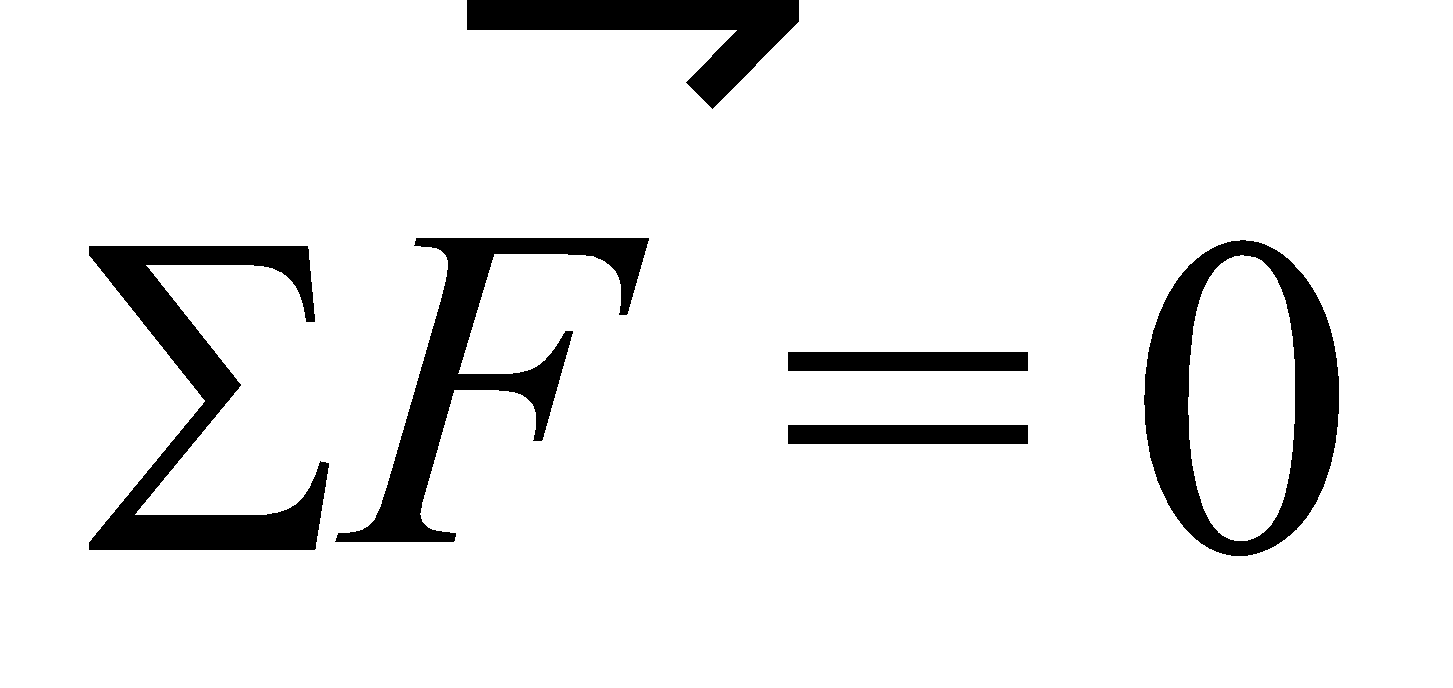  
Then   and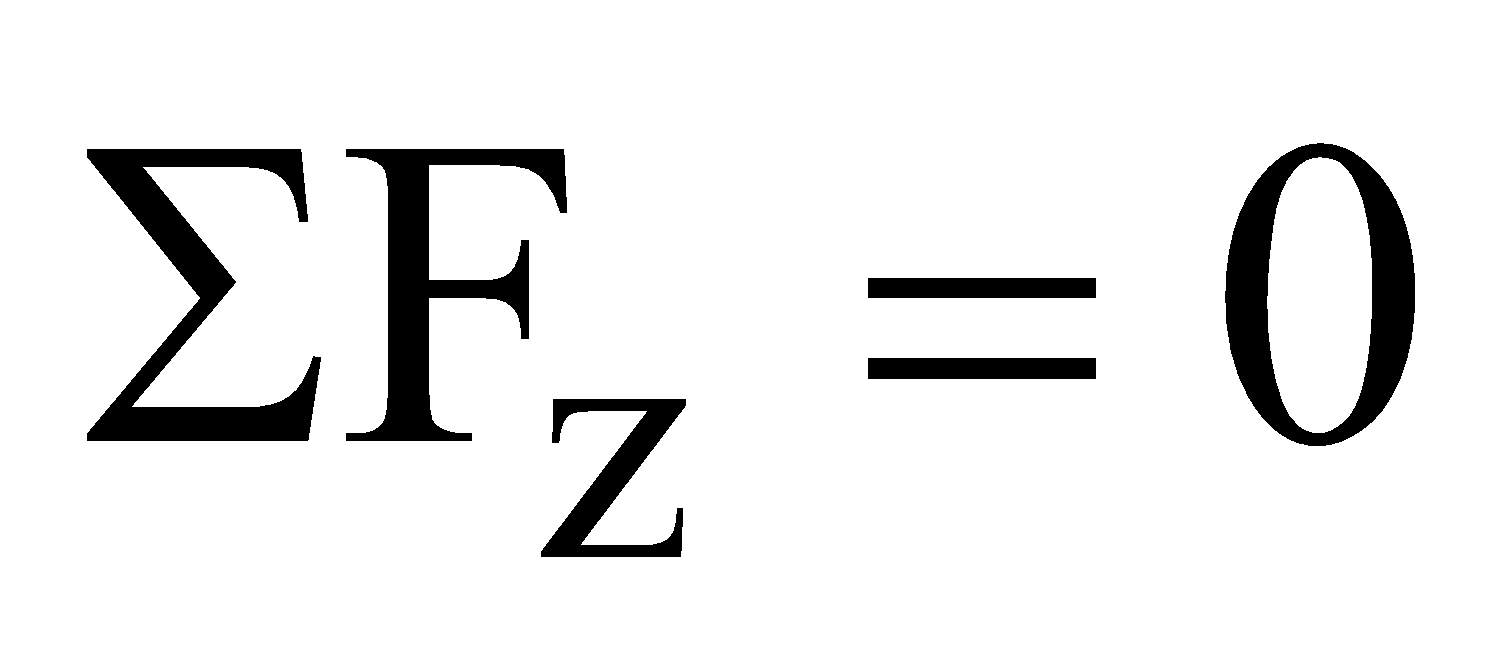

STABLE EQUILIBRIUM

If a body is slightly displaced from equilibrium position, it has the tendency to regain its original position, it is said to be in stable equilibrium.
In this case, P.E. is minimum.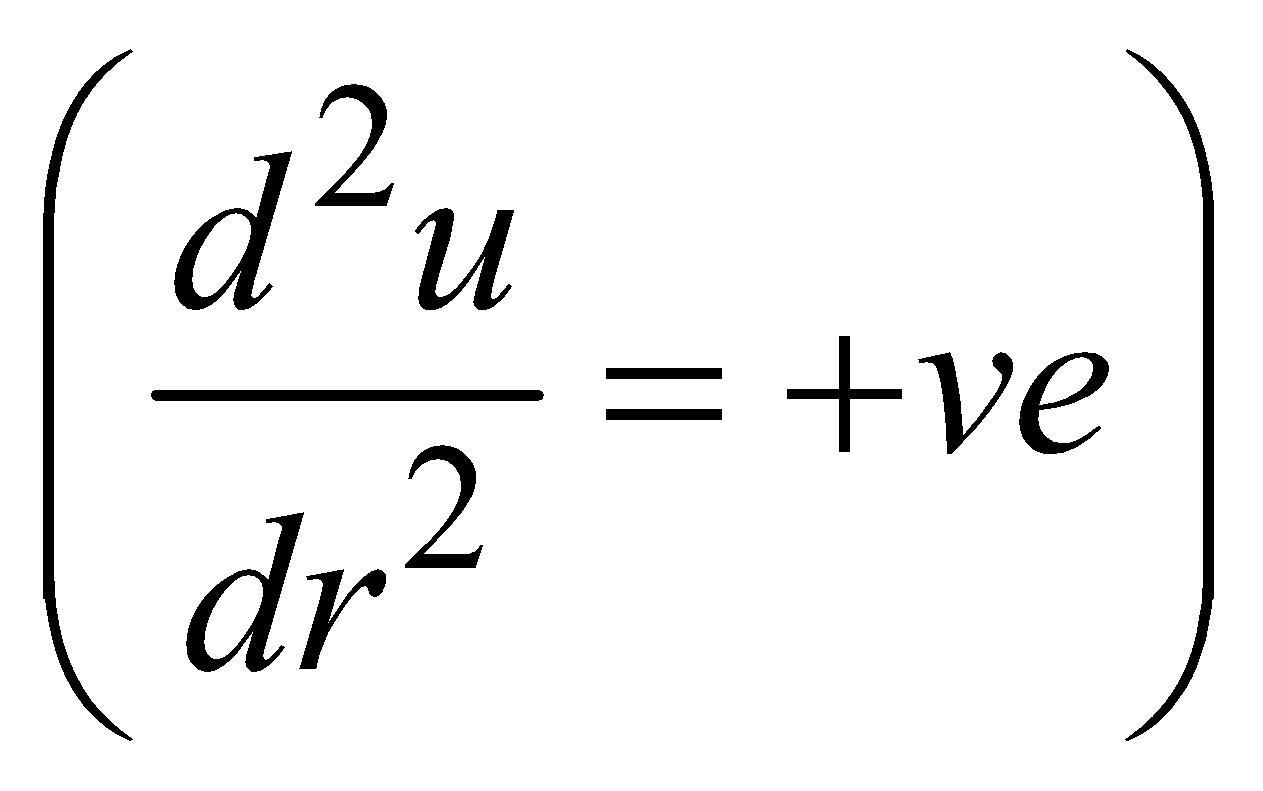
So, the centre of gravity is lowest.

UNSTABLE EQUILIBRIUM

If a body, after being displaced from the equilibrium position, moves in the direction of displacement, it is said to be in unstable equilibrium.
In this case, P.E. is maximum.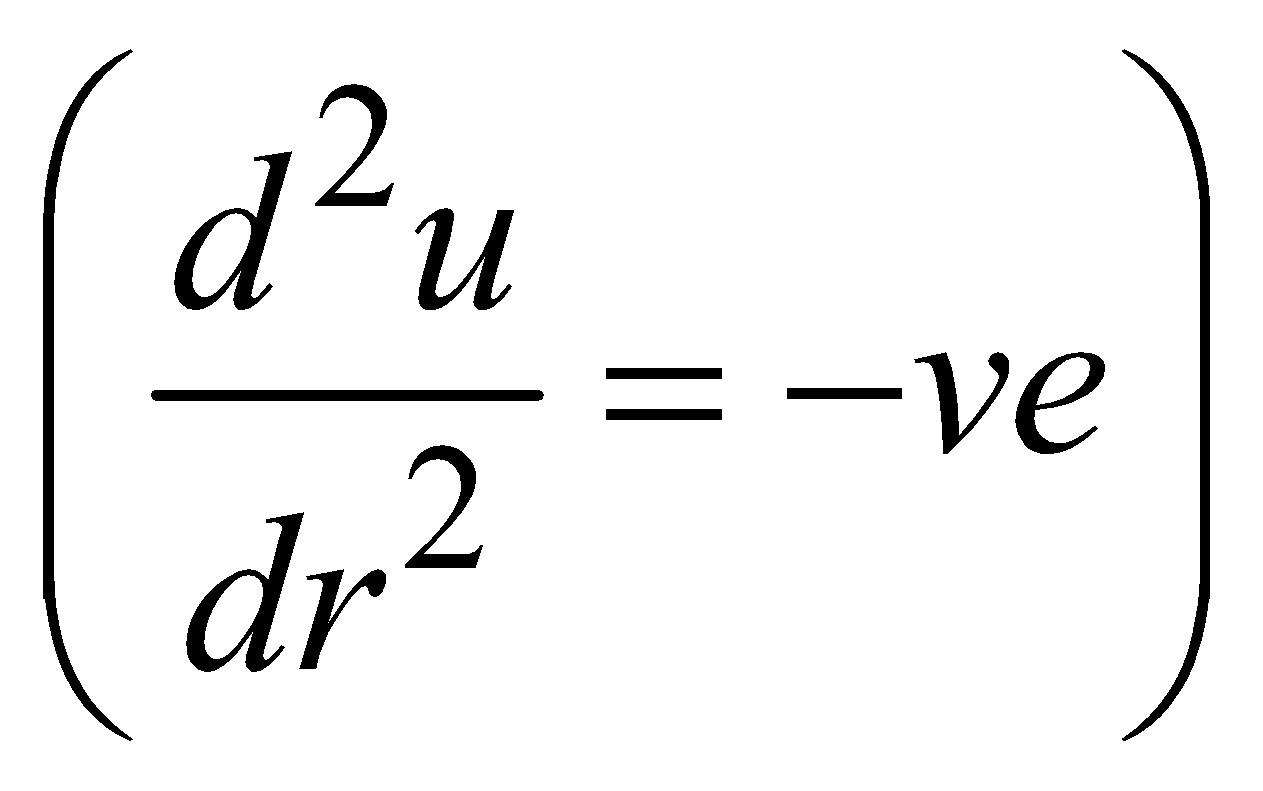
So, the centre of gravity is highest.

NEUTRAL EQUILIBRIUM

If a body, after being slightly displaced from the equilibrium position has no tendency to come back or to move in the direction of displacement the equilibrium is known to be neutral.
In this case,  P.E. is constant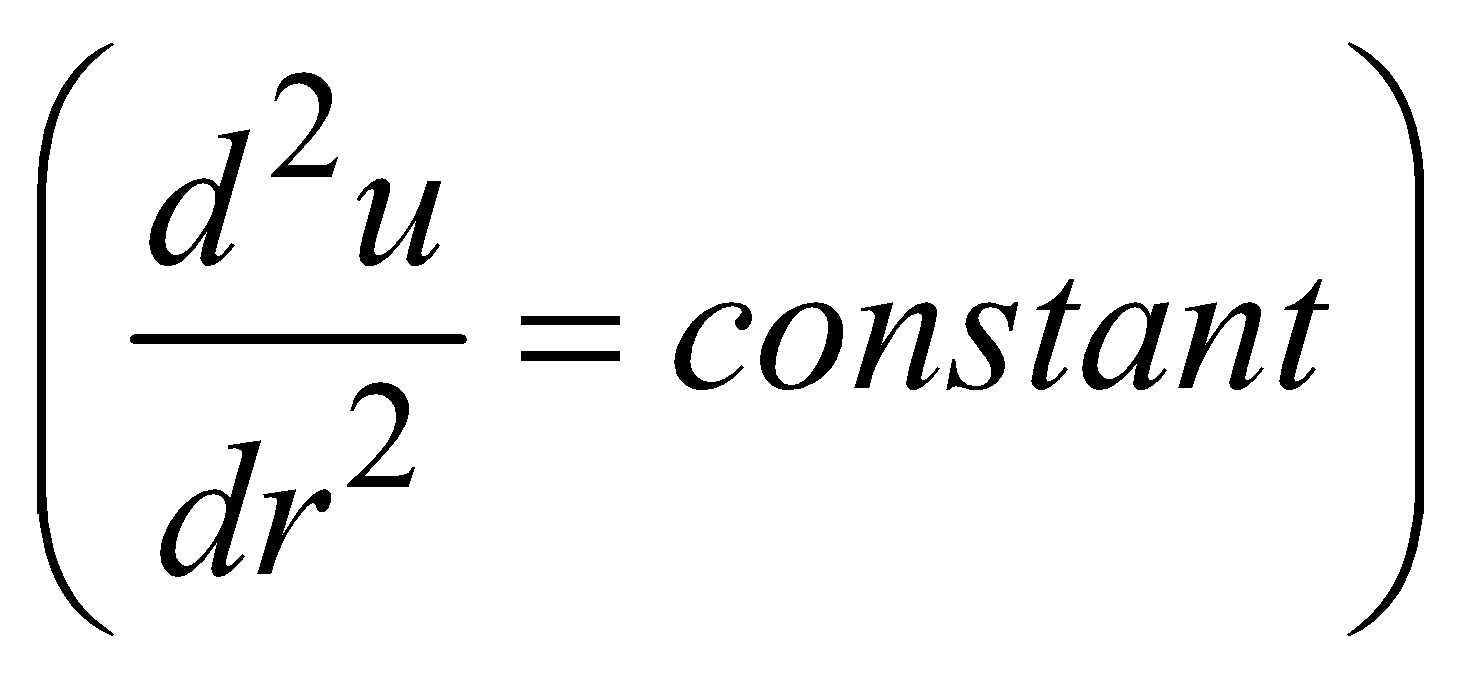
The centre of gravity remains at constant height.

 

Application of Newton’s Laws

Free body diagram of a mass is a separate diagram of that mass. All forces acting on the mass are sketched. A FBD is drawn to visualise the direct forces acting on a body.

 

Case 1 : Masses M1 and M2 are tied to a string, which goes over a frictionless pulley
  1. If M2 > M1 and they move with acceleration a
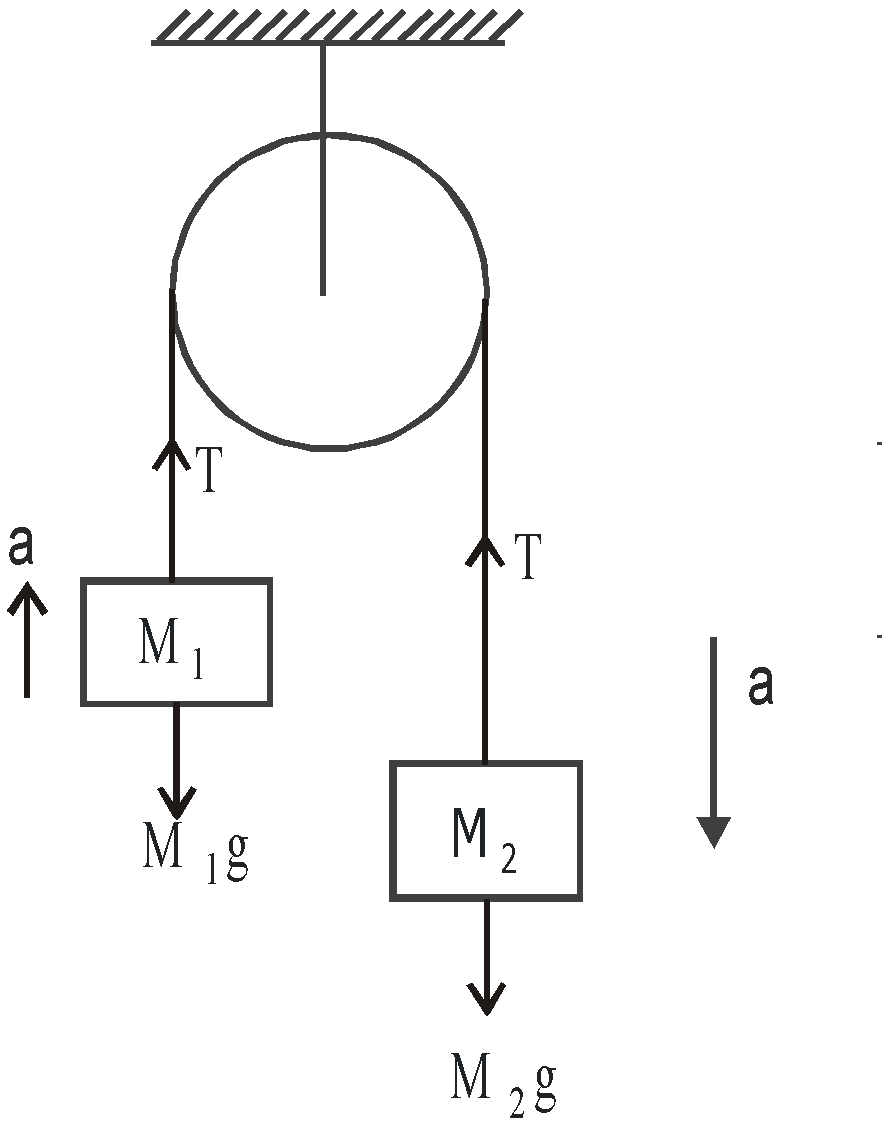
FBD of M1,  FBD of M2
 
 
where T is the tension in the string.
It gives 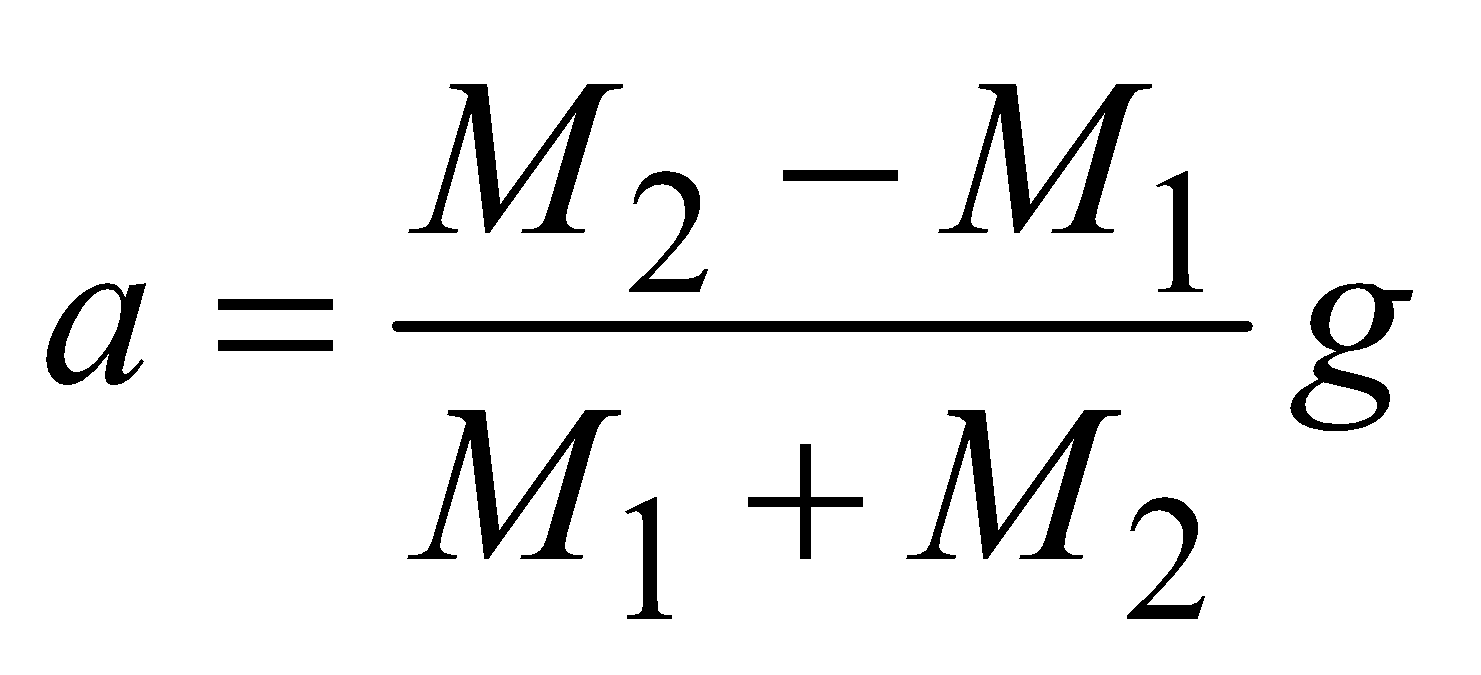and
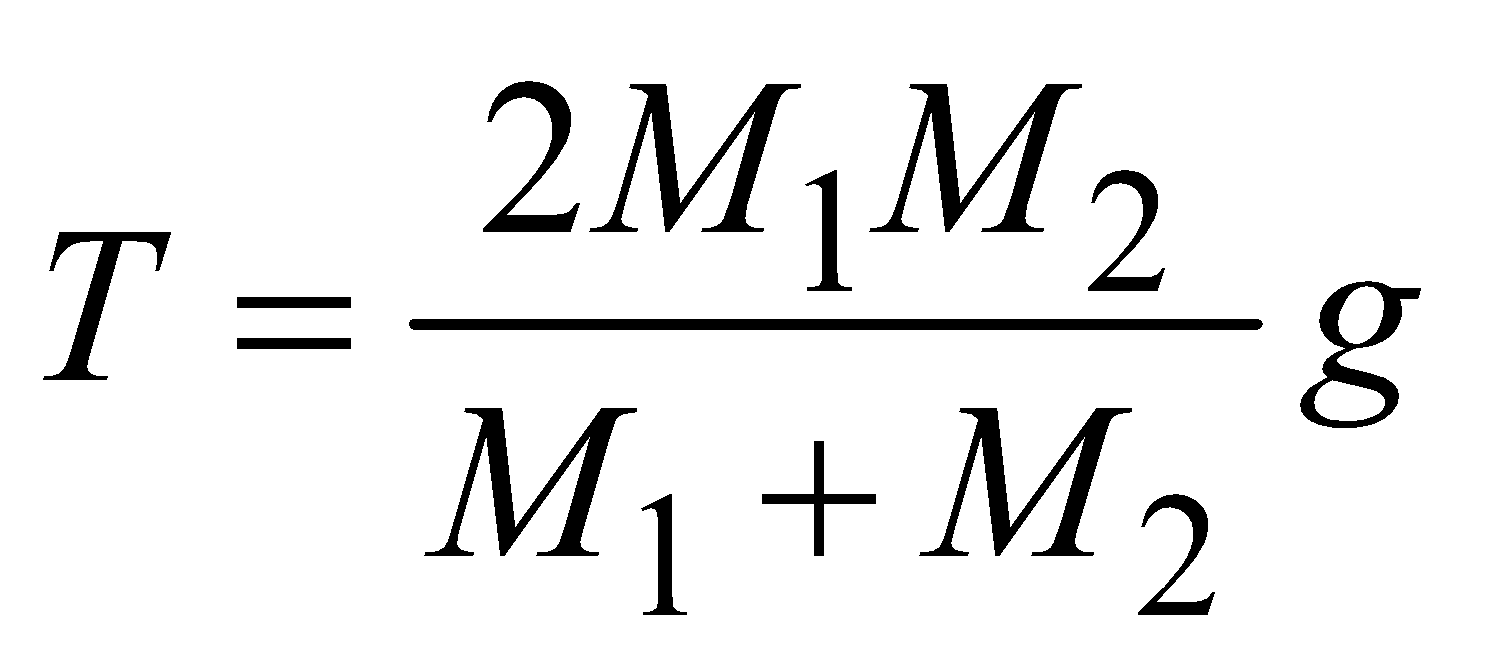
  1. If the pulley begins to move with acceleration f, downwards
 and

 

Case 2 : Three masses M1, M2 and M3 are connected with strings as shown in the figure and lie on a frictionless surface. They are pulled with a force F attached to M1.
The forces on M2 and M3 are as follows
and ;    
Acceleration of the system is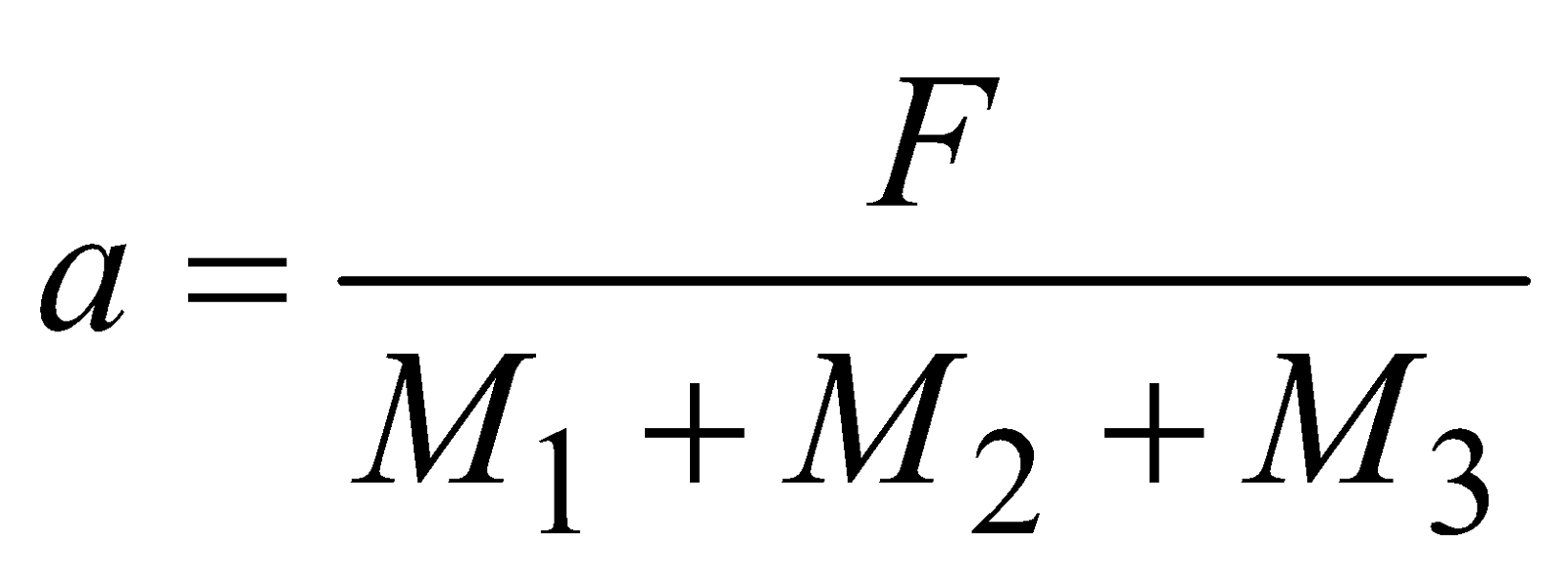

 

Case 3 :  Two blocks of masses M1 and M2 are suspended vertically from a rigid support with the help of strings as shown in the figure. The mass M2 is pulled down with a force F.
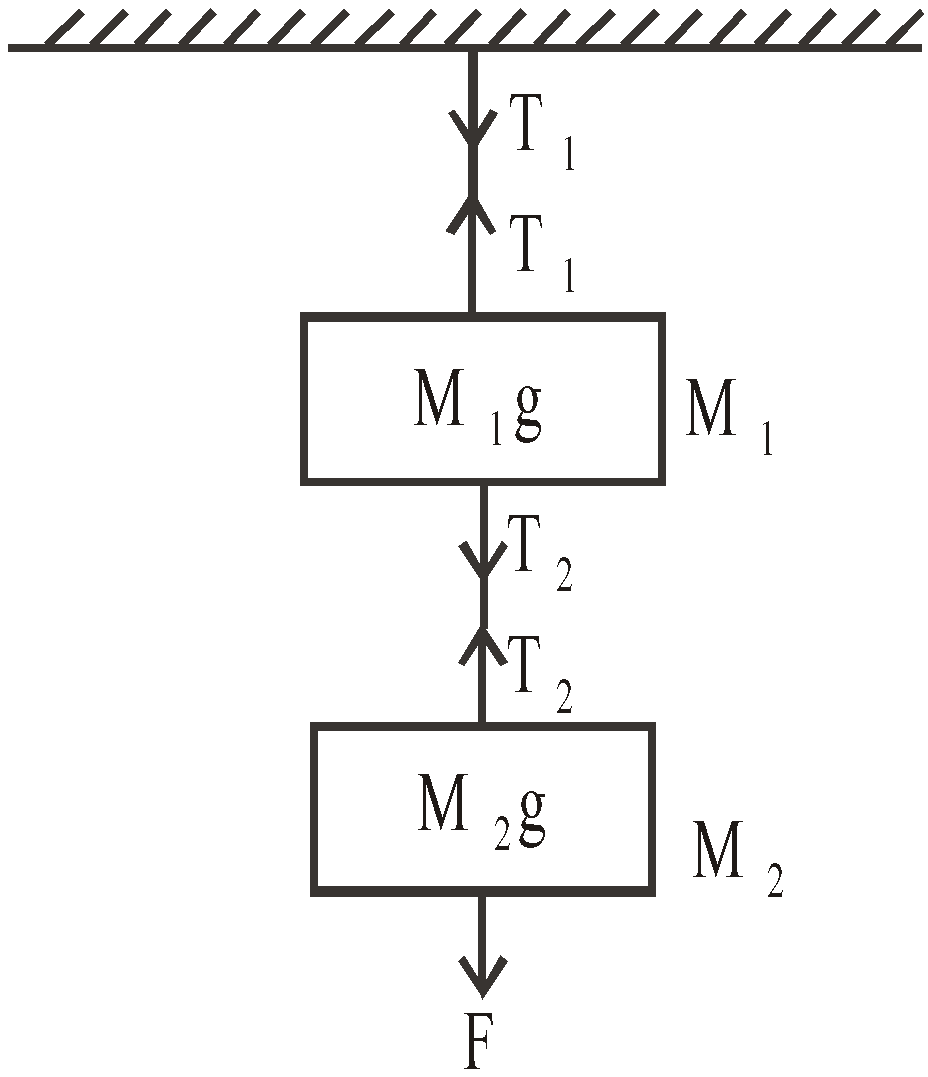
The tension between the masses M1 and M2 will be T2 = F + M2g
Tension between the support and the mass M1 will be T1 = F + (M1 + M2)g

 

Case 4 : Two masses M1 and M2 are attached to a string which passes over a pulley attached to the edge of a horizontal table. The mass M1 lies on the frictionless surface of the table.
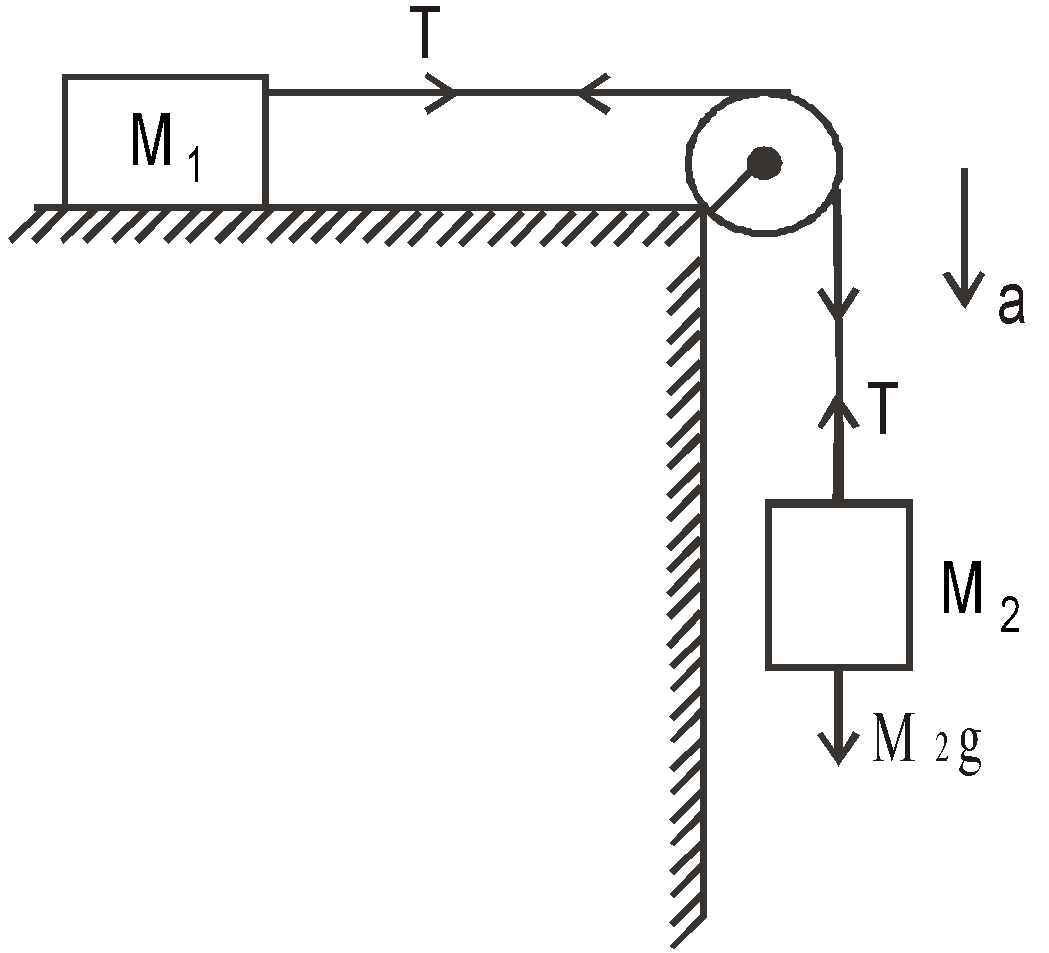
Let the tension in the string be T and the acceleration of the system be a. Then
T = M1a …(1)
M2g – T = M2a …(2)
Adding eqns. (1) and (2), we get
and

 

Case 5 : Two masses M1 and M2 are attached to the ends of a string, which passes over a frictionless pulley at the top of the inclined plane of inclination θ. Let the tension in the string be T.
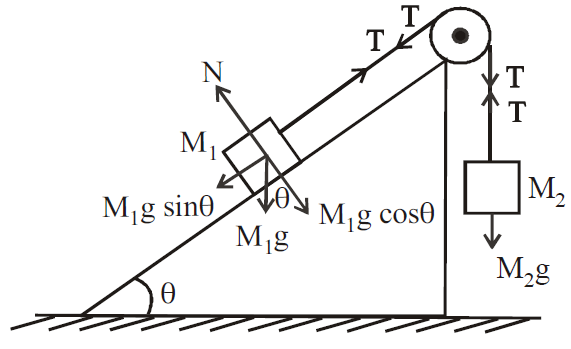
  1. When the mass M1 moves upwards with acceleration a.
From the FBD of M1 and M2,
T – M1g sin θ = M1a  …(1)
M2g – T = M2a …(2)
Solving eqns. (1) and (2) we get,
FBD of mass M1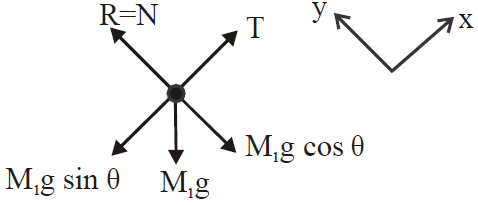   
  1. When the mass M1 moves downwards with acceleration a.
Equation of motion for M1 and M2,
M1g sin θ – T = M1a …(1)
T – M2g = M2a …(2)
Solving eqns. (1) and (2) we get,

 

  • If (M2/M1 = sinθ) then the system does not accelerate.
  • Changing position of masses, does not affect the tension. Also, the acceleration of the system remains unchanged.
  • If M1 = M2 = M (say), then

 

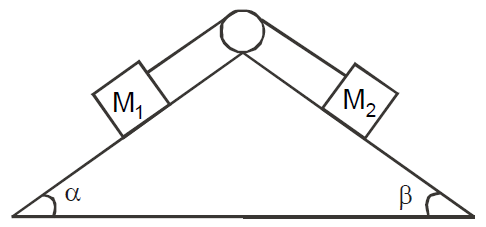
Case 6 : Two masses M1 and M2 are attached to the ends of a string over a pulley attached to the top of a double inclined plane of angle of inclination α and β.
Let M2 move downwards with acceleration a and the tension in the string be T then
FBD of M1
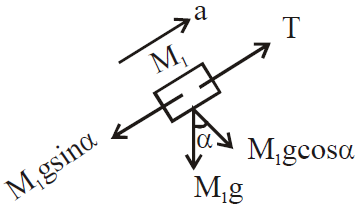
Equation of motion for M1
T – M1g sin α = M1a
or T = M1g sin α + M1a …(1)

 

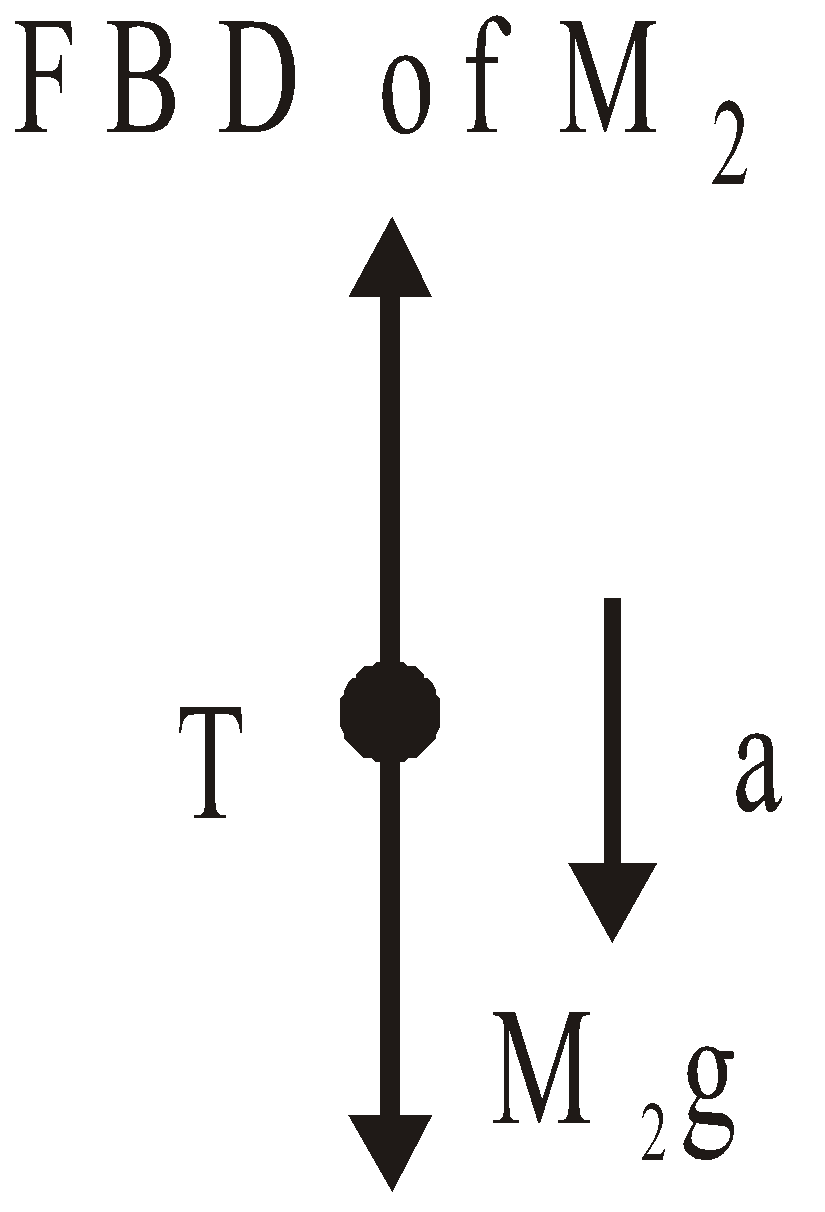
FBD of M2   
  
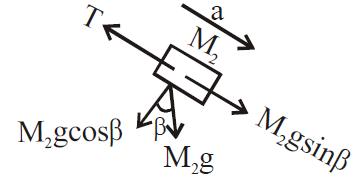
Equation of motion for M2
M2g sinβ – T = M2a
or   T = M2g sin β  – M2a …(2)
Using eqn. (1) and (2) we get,
M1g sin α + M1a = M2g sin β – M2a
Solving we get,  
and

 

Case 7 : A person/monkey climbing a rope

 

  • A person of mass M climbs up a rope with acceleration a. The tension in the rope will be M(g+a).
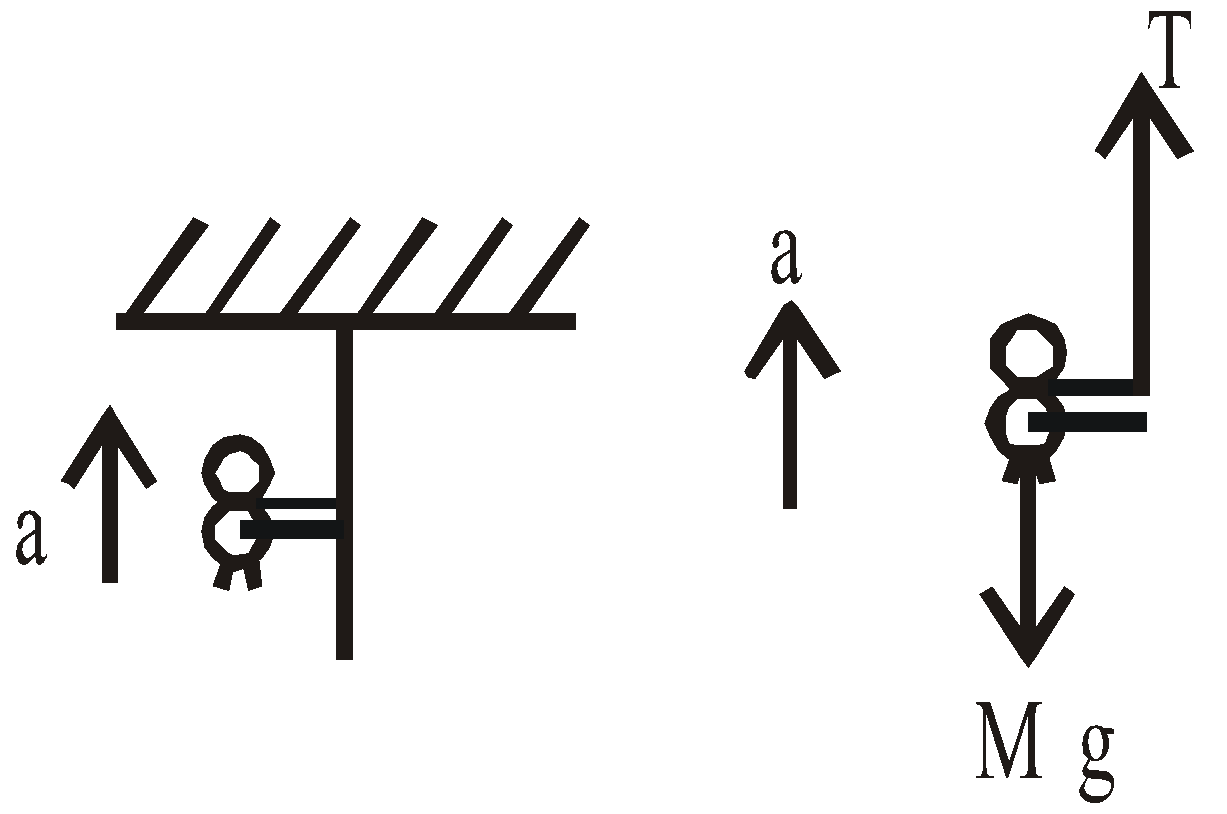
T – Mg = Ma ⇒ T = M(g + a)
  • If the person climbs down along the rope with acceleration a, the tension in the rope will be M(g–a).
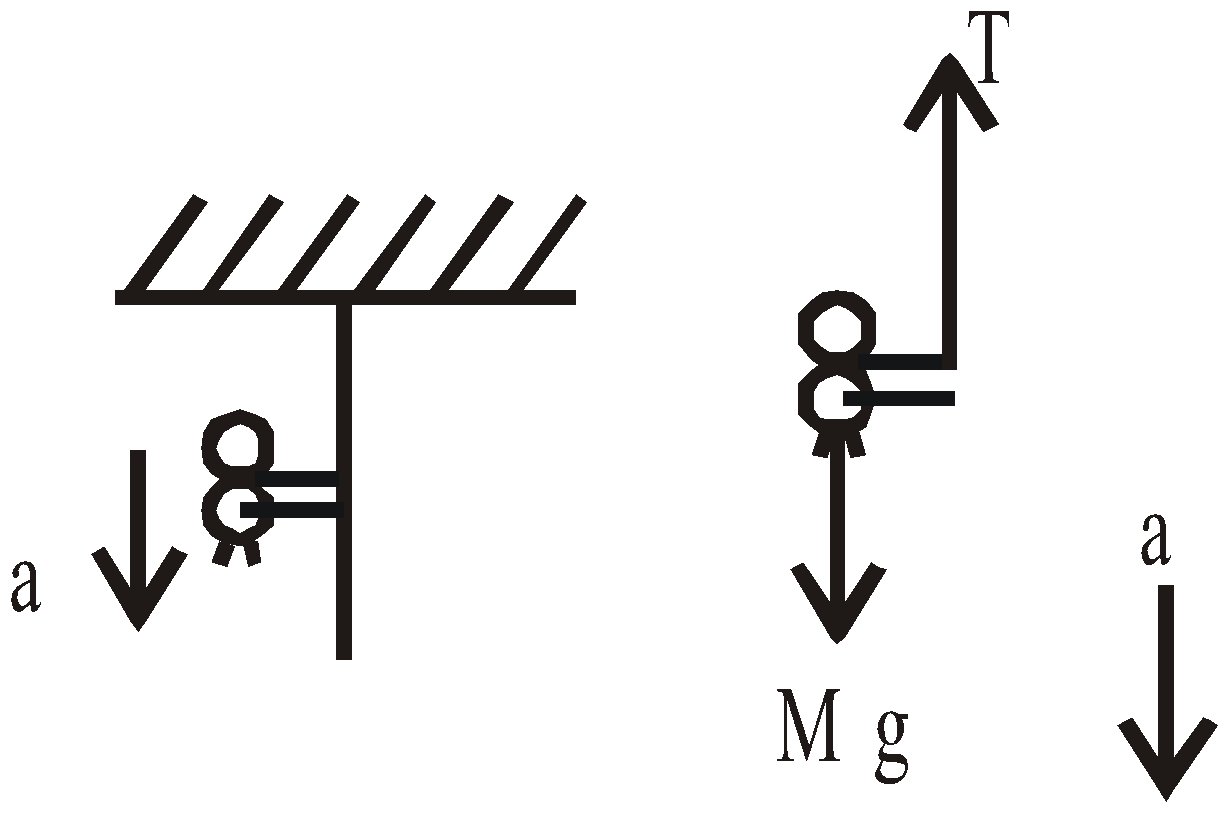
Mg – T = Ma ⇒ T = M(g – a)
  • When the person climbs up or down with uniform speed, tension in the string will be Mg.

 

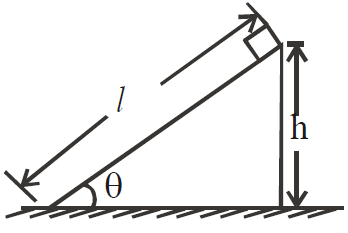
Case 8 : A body starting from rest moves along a smooth inclined plane of length l, height h and having angle of inclination θ.
FBD of body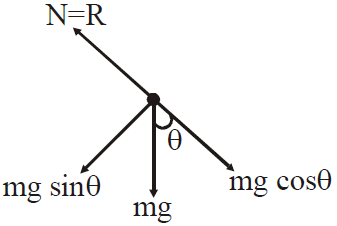
 
(where N=R is normal reaction applied by plane on the body of mass m)
For downward motion, along the inclined plane,
By work-energy theorem loss in P.E. = gain in K.E.
Also, from the figure, h = l sin θ.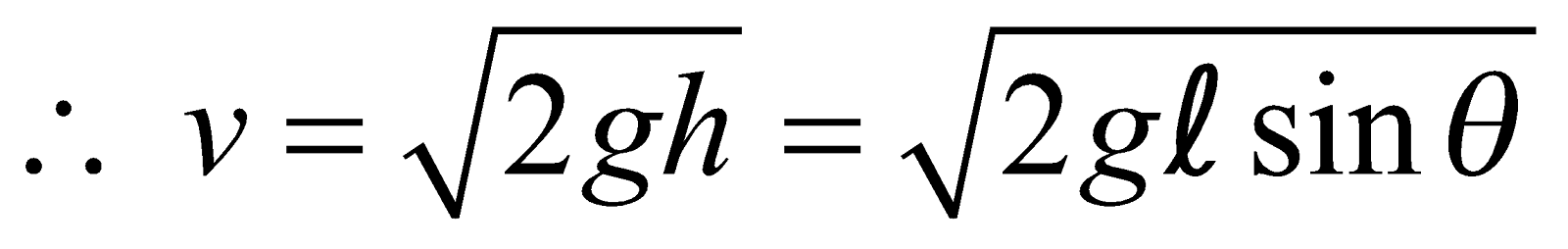      
  • Acceleration down the plane is g sin θ.
  • Its velocity at the bottom of the inclined plane will be
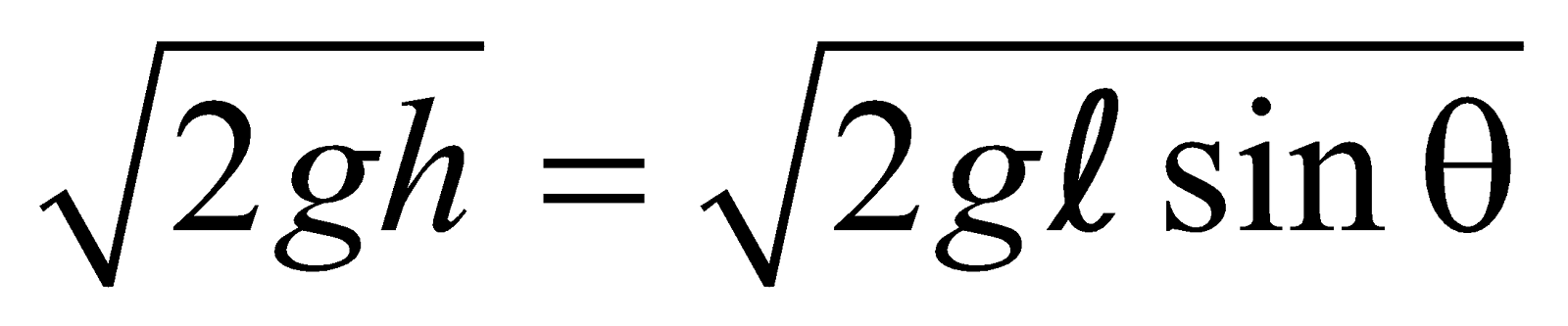
  • Time taken to reach the bottom will be  
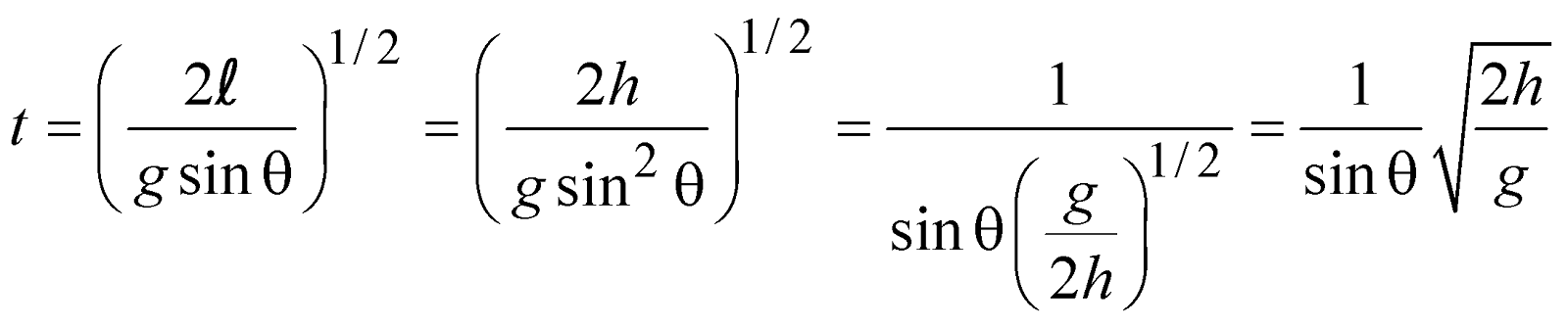
  • If angles of inclination are θ1 and θ2 for two inclined planes  
Keeping the length constant then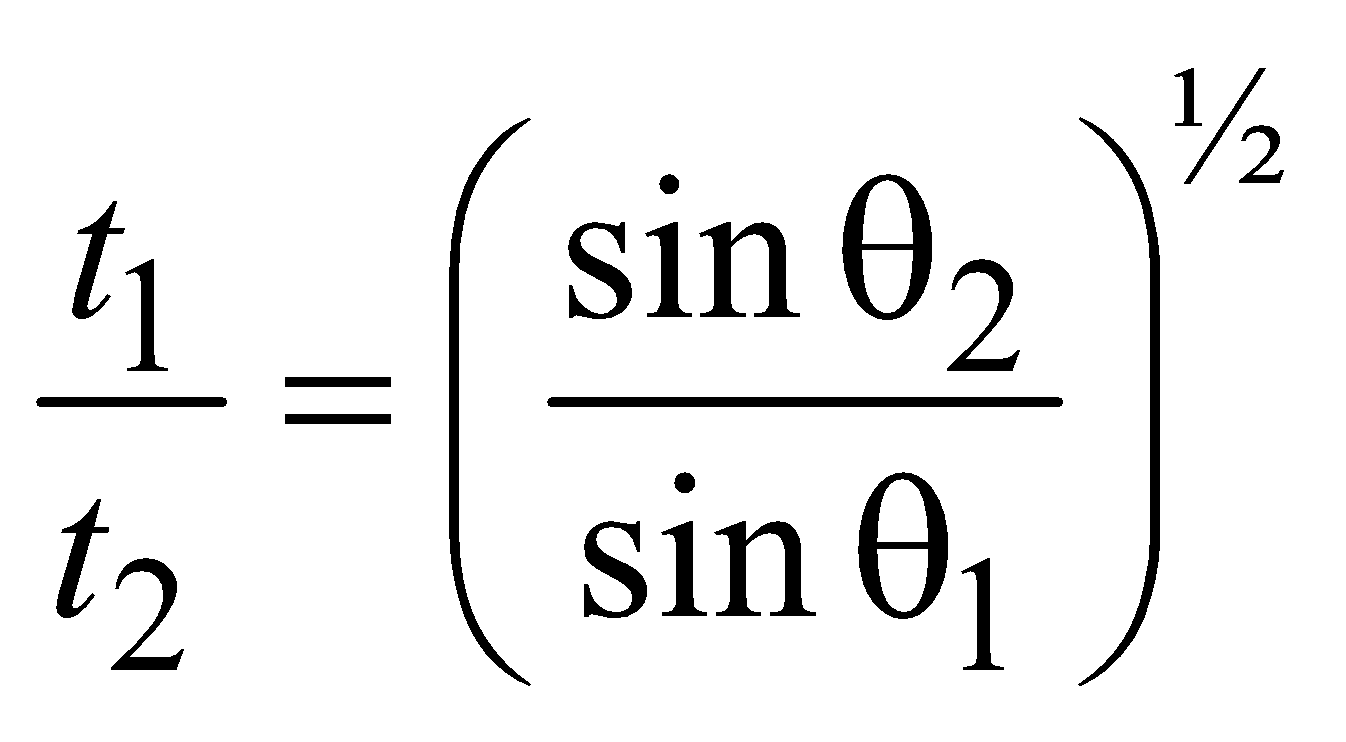

 

Case 9 : Weight of  a man in a lift :
  1. When lift is accelerated upward
In this case the man also moves in upward direction with an acceleration
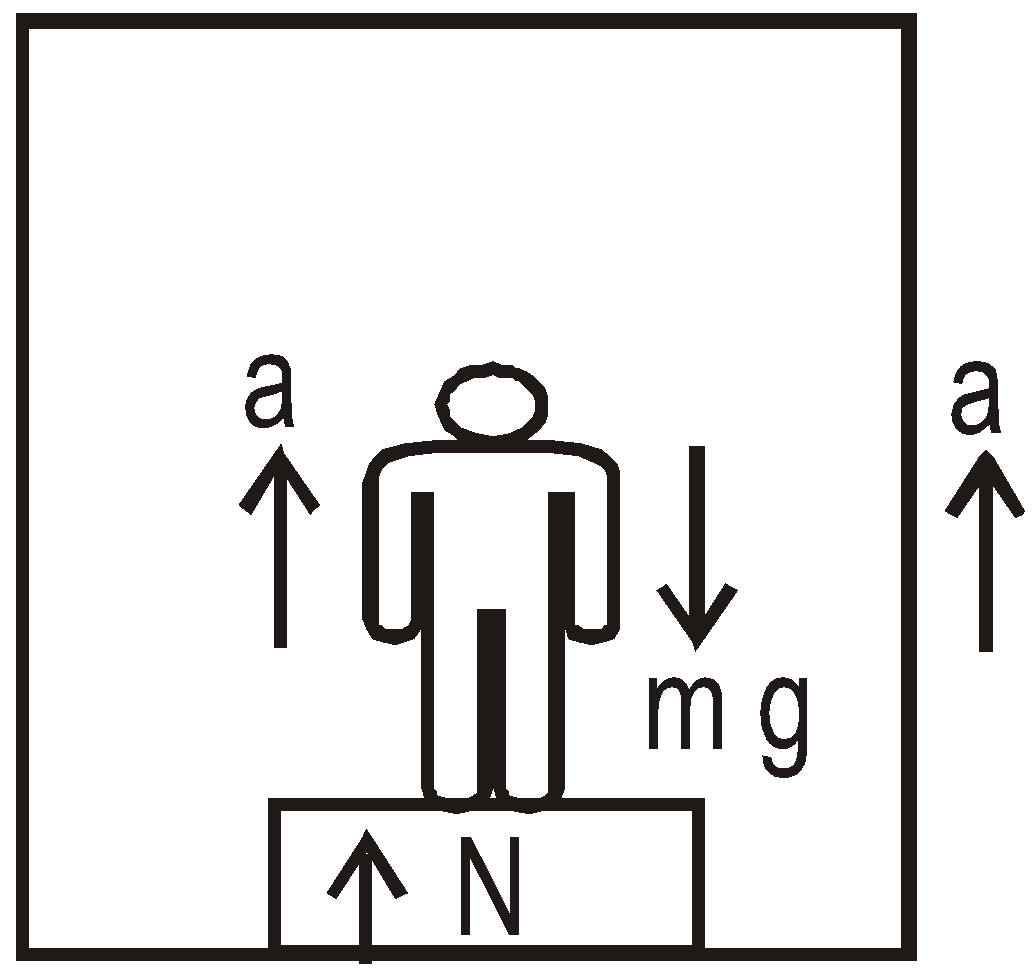
Then from Newton’ second law
N – mg = ma or N = m(g + a)
or Wapp = m(g + a) 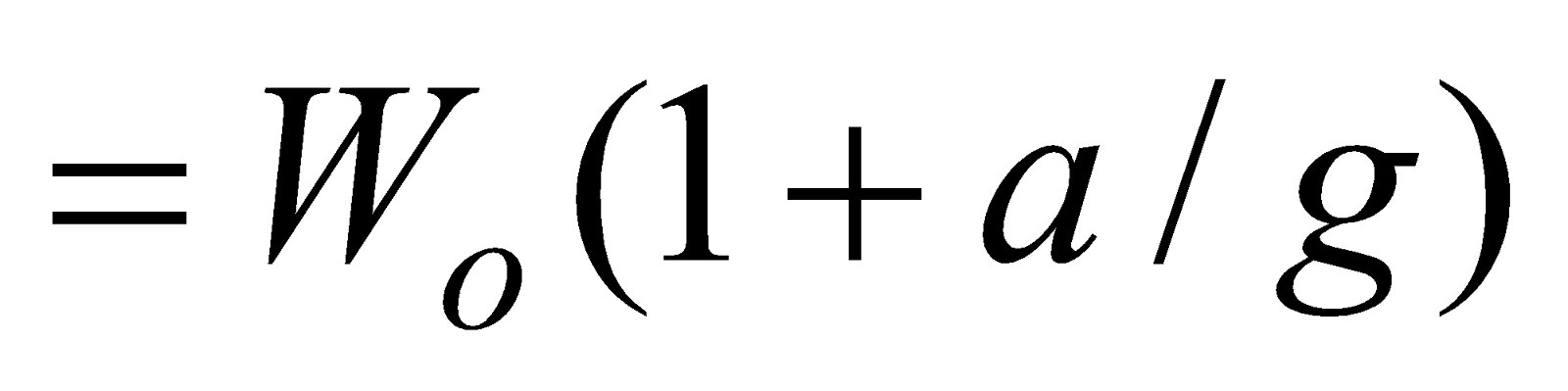(as W = mg)
Where Wapp is apparent weight of the man in the lift, Wo is the real weight, N is the reaction of lift on the man. It is clear that N = Wapp
When the lift moves upward and if we measure the weight of the man by any means (such as spring balance) then we observe more weight (i.e., Wapp) than the real weight (Wo) Wapp >Wo
  1. When lift is accelerated downward
In this case from Newton’s second law
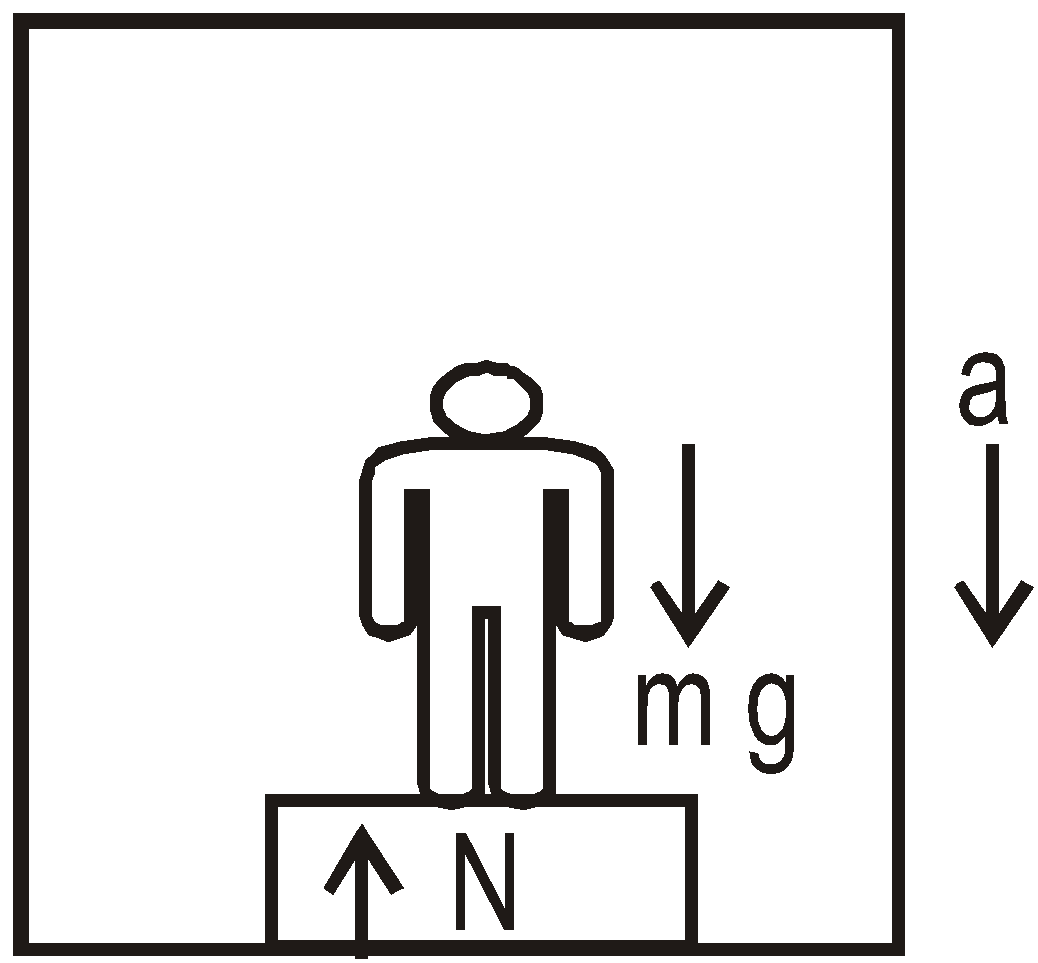
mg – N = ma
or N = m(g – a) = Wo(1– a/g)
or W’app= Wo(1– a/g)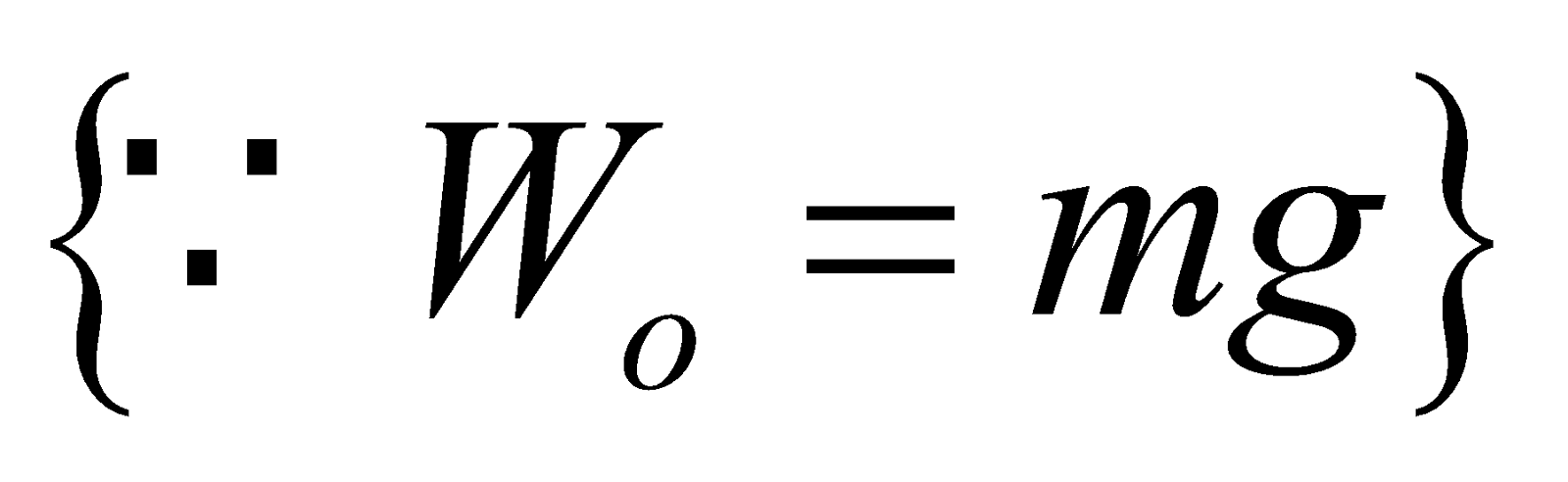  
If we measure the weight of man by spring balance, we observe deficiency because Wapp< Wo.

 

  1. When lift is at rest or moving with constant velocity
From Newton’s second law   
N –mg = 0  or N = mg
In this case spring balance gives the true weight of the man.
 
case 10 Acceleration of block pushing on block
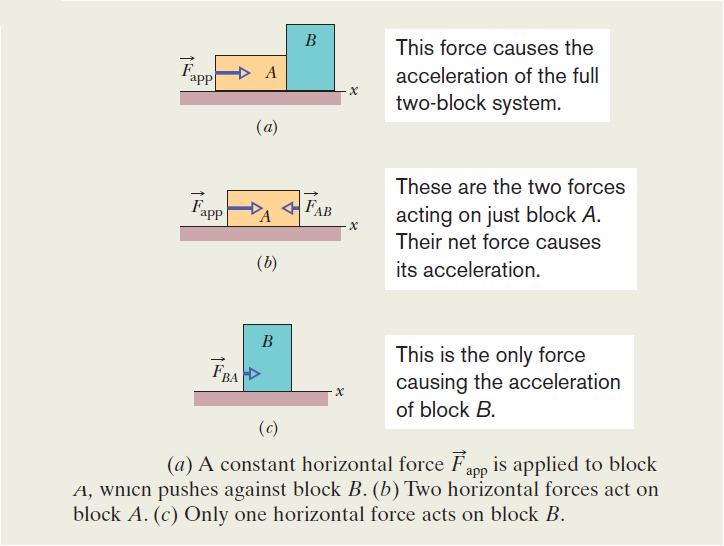
Solution:
Because of the direction in which force \( \vec{F_{app}} \) is applied, the two blocks form a rigidly connected system. We can relate the net force on the system to the acceleration of the system with Newton’s second law. Here, once again for the x axis, we can write that law as 
\(F_{app} =(m_A+m_B)a\)
where now we properly apply \(F_{app}\) to the system with total mass \(m_A+m_B\). Solving for a and substituting known values, we find
\(a=\frac{F_{app}}{m_A+m_B}\)
Case 11 : Three masses M1, M2 and M3 are placed on a smooth surface in contact with each other as shown in the figure. A force F pushes them as shown in the figure and the three masses move with acceleration a,
 ⇒ F – F1 = m1a …(i)
 ⇒ F1 – F2 = m2a …(ii)
 ⇒ F2 = M3 a …(iii)
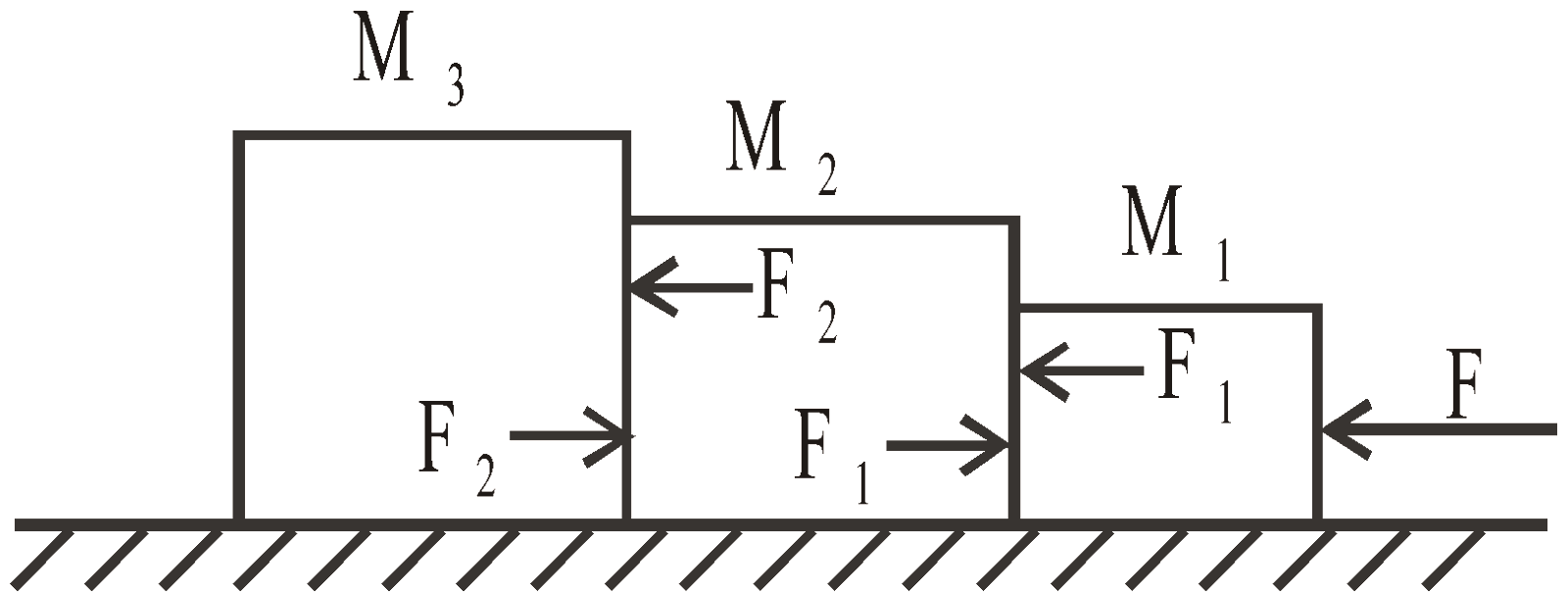
Adding eqns. (i), (ii) and (iii) we get,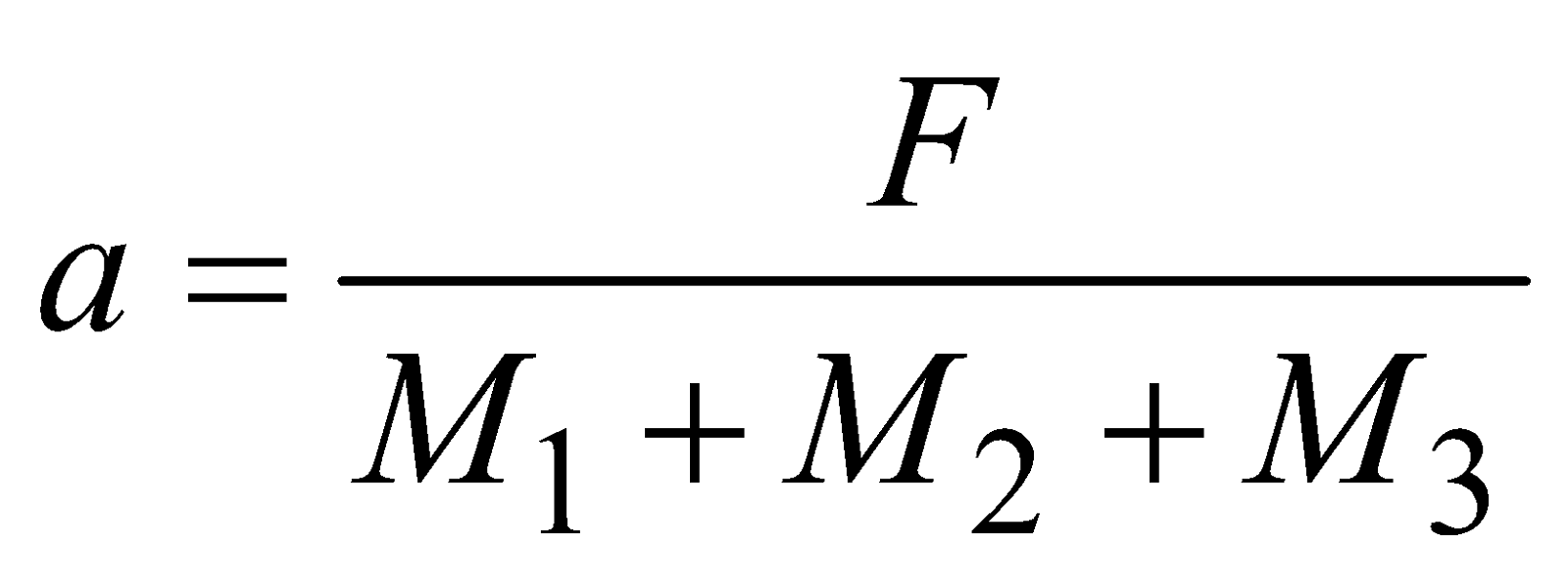
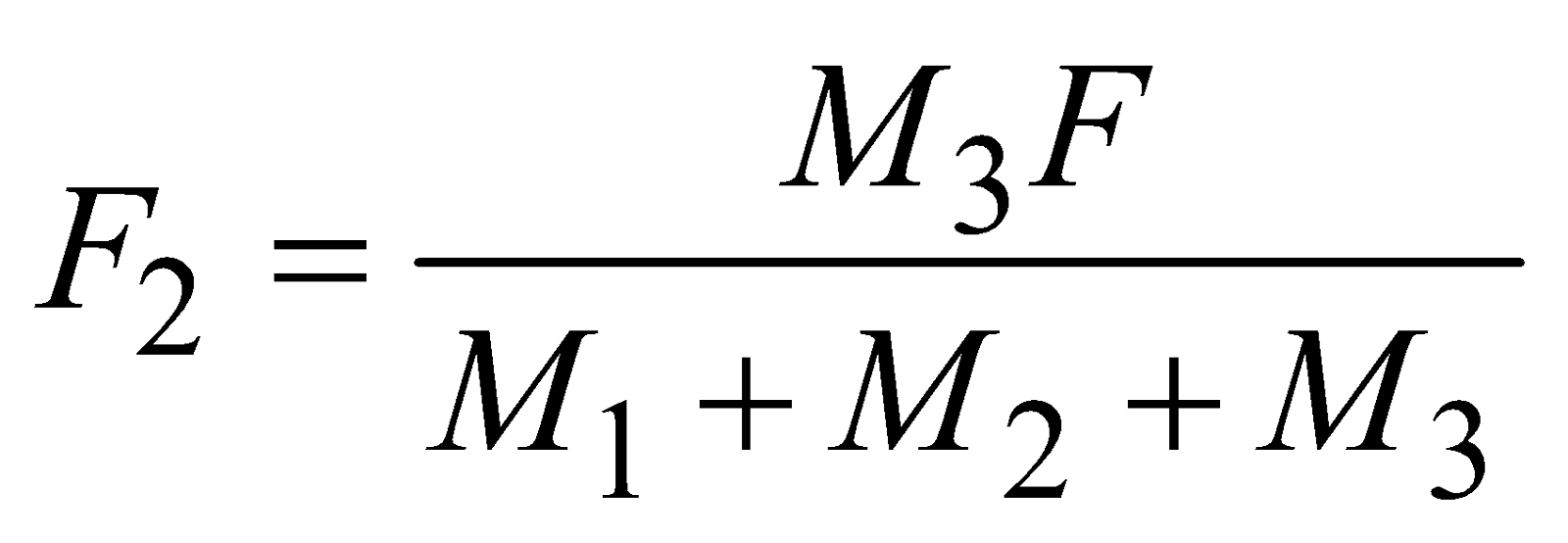⇒ and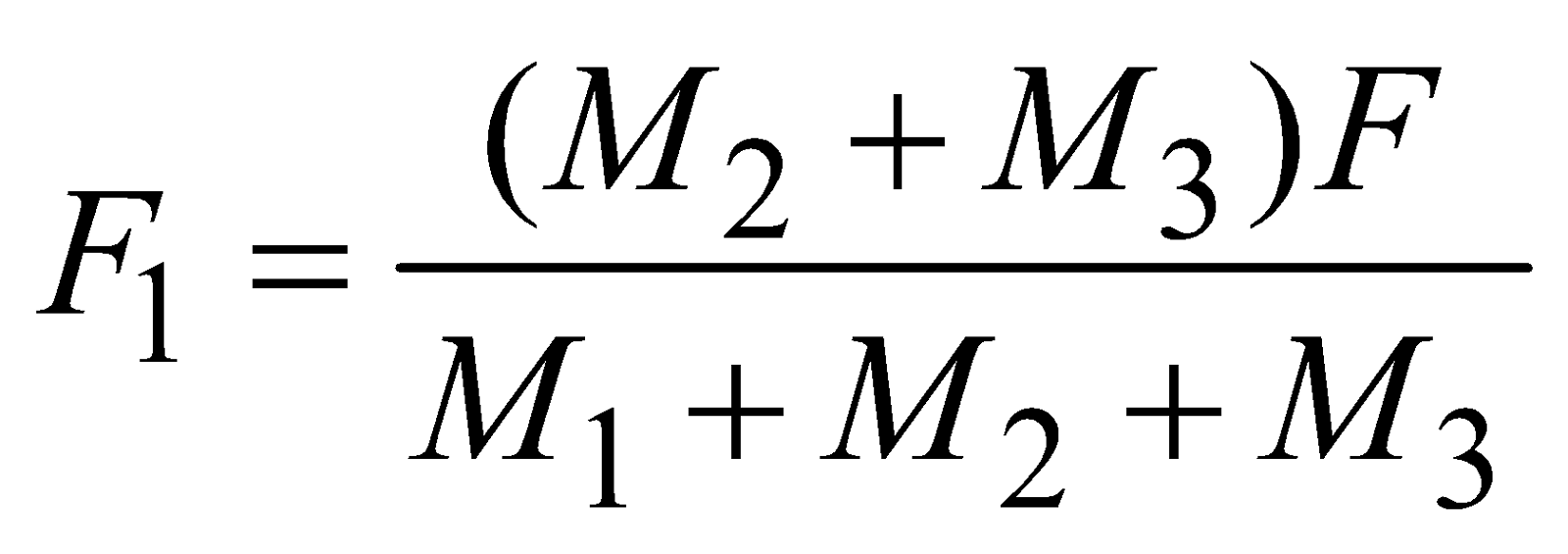

 

KEEP IN MEMORY
    • When a man jumps with load on his head, the apparent weight of the load and the man is zero.
    • If a person sitting in a train moving with uniform velocity throws a coin vertically up, then coin will fall back in his hand.
    • If the train is uniformly accelerated, the coin will fall behind him.
    • If the train is retarded uniformly, then the coin will fall in front of him.
Scroll to Top