IBDP Physics 2025 SL&HL: 3.2 Conservation of energy Study Notes

IB DP PhysicsIB DP MathsIB DP ChemistryIB DP Biology

IBDP Physics 2025 -Study Notes -All Topics

Learning Objectives

Students should understand:
• the principle of the conservation of energy
• that work done by a force is equivalent to a transfer of energy
• that energy transfers can be represented on a Sankey diagram
• that work W done on a body by a constant force depends on the component of the force along the line of displacement s is  given by W = Fs cos θ
• that work done by the resultant force on a system is equal to the change in the energy of the system
• that mechanical energy is the sum of kinetic energy, gravitational potential energy and elastic potential energy
• that in the absence of frictional, resistive forces, the total mechanical energy of a system is conserved
• that if mechanical energy is conserved, work is the amount of energy transformed between different forms of mechanical energy in a system, such as:
◦  the kinetic energy of translational motion as given by \(E_k=\frac{1}{2}mv^2 =\frac{p^2}{2m}\)
◦ the gravitational potential energy, when close to the surface of the Earth as given by ΔEp = mgΔh
◦ the elastic potential energy as given by \(E_H=\frac{1}{2}k(\Delta x)^2\)
• that power developed P is the rate of work done, or the rate of energy transfer, as given by \(p=\frac{\Delta W}{\Delta t}=Fv\)
• efficiency η in terms of energy transfer or power as given by \(\eta=\frac{E_{output}}{E_{input}}=\frac{P_{output}}{P_{input}}\)
• energy density of the fuel sources.

WORK-ENERGY THEOREM

Let a number of forces acting on a body of mass m have a resultant force and by acting over a displacement x (in the direction of ), does work on the body, and there by changing its velocity from u (initial velocity) to v (final velocity). Kinetic energy of the body changes.
So, work done by force on the body is equal to the change in kinetic energy of the body.
This expression is called Work energy (W.E.) theorem.

LAW OF CONSERVATION OF MECHANICAL ENERGY

The sum of the potential energy and the kinetic energy is called the total mechanical energy.
The total mechanical energy of a system remains constant if only conservative forces are acting on a system of particles and the work done by all other forces is zero.
i.e., ΔK + ΔU = 0
or  Kf – Ki + Uf – Ui = 0
or  Kf + Uf = Ki + Ui = constant

LAW OF CONSERVATION OF ENERGY

Energy is of many types – mechanical energy, sound energy, heat energy, light energy, chemical energy, atomic energy, nuclear energy etc.

 

In many processes that occur in nature energy may be transformed from one form to other. Mass can also be transformed into energy and vice-versa. This is according to Einstein’s mass-energy equivalence relation,  E = mc2.
In dynamics, we are mainly concerned with purely mechanical energy.

 

The study of the various forms of energy and of transformation of one kind of energy into another has led to the statement of a very important principle, known as the law of conservation of energy.

 

“Energy cannot be created or destroyed, it may only be transformed from one form into another. As such the total amount of energy never changes”.

 

KEEP IN MEMORY
  1. Work done against friction on horizontal surface = μ mgx and work done against force of friction on inclined plane = (μmg cosθ) x where μ = coefficient of friction.
  2. If a body moving with velocity v comes to rest after covering a distance ‘x’ on a rough surface having coefficient of friction μ, then (from work energy theorem), 2μ gx = v2. Here retardation is
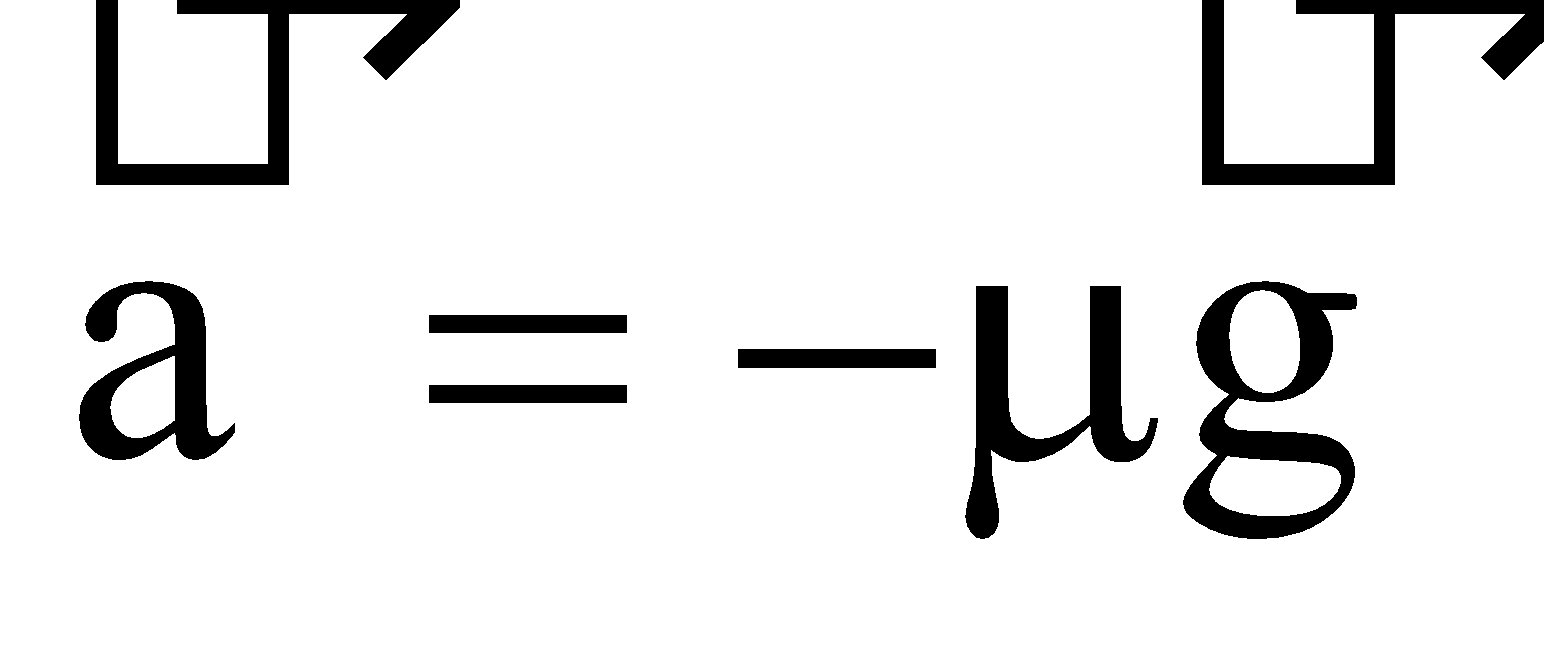
  3. Work done by a centripetal force is always zero.
  4. Potential energy of a system decreases when a conservative force does work on it.
  5. If the speed of a vehicle is increased by n times, then its stopping distance becomes n2 times and if momentum is increased by n times then its kinetic energy increases by n2 times.
  6. Stopping distance of the vehicle
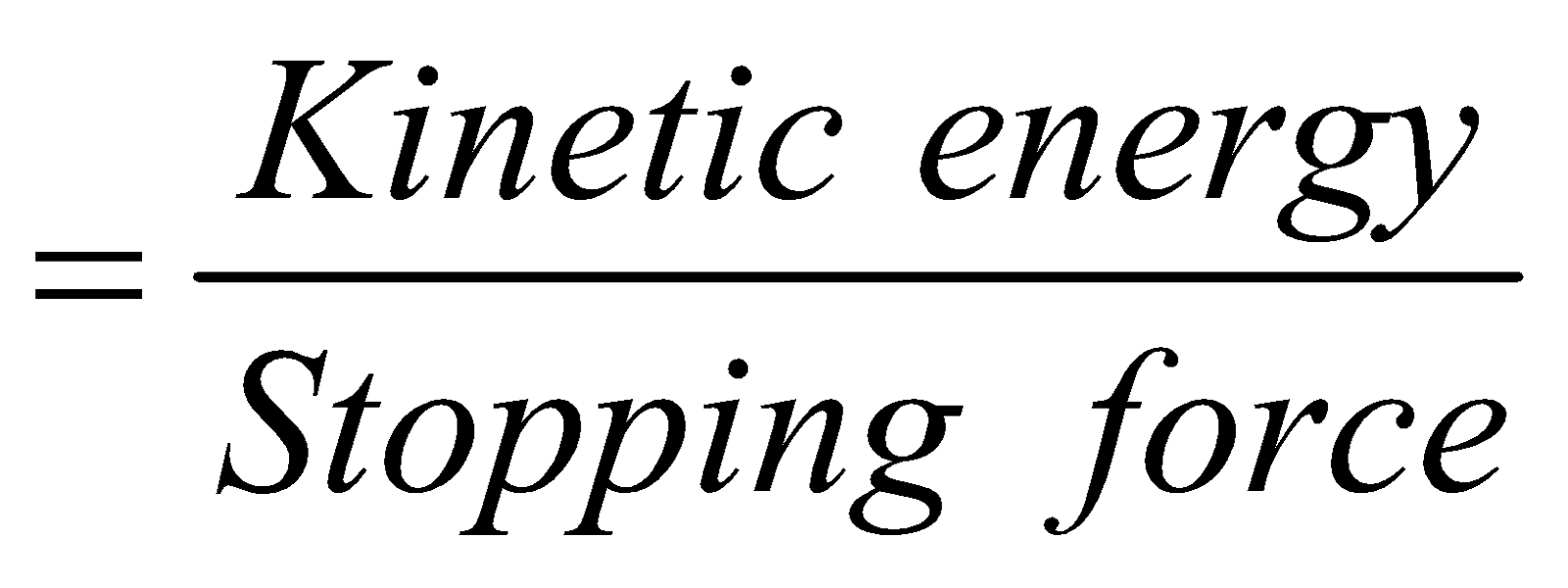
  7. Two vehicles of masses M1 and M2 are moving with velocities u1 and u2 respectively. When they are stopped by the same force, their stopping distance are in the ratio as follows :
    Since the retarding force F is same in stopping both the vehicles. Let x1 and x2 are the stopping distances of vehicles of masses M1 & M2 respectively, then
 ….(i)
where u1 and u2 are initial velocity of mass M1 & M2 respectively & final velocity of both mass is zero.
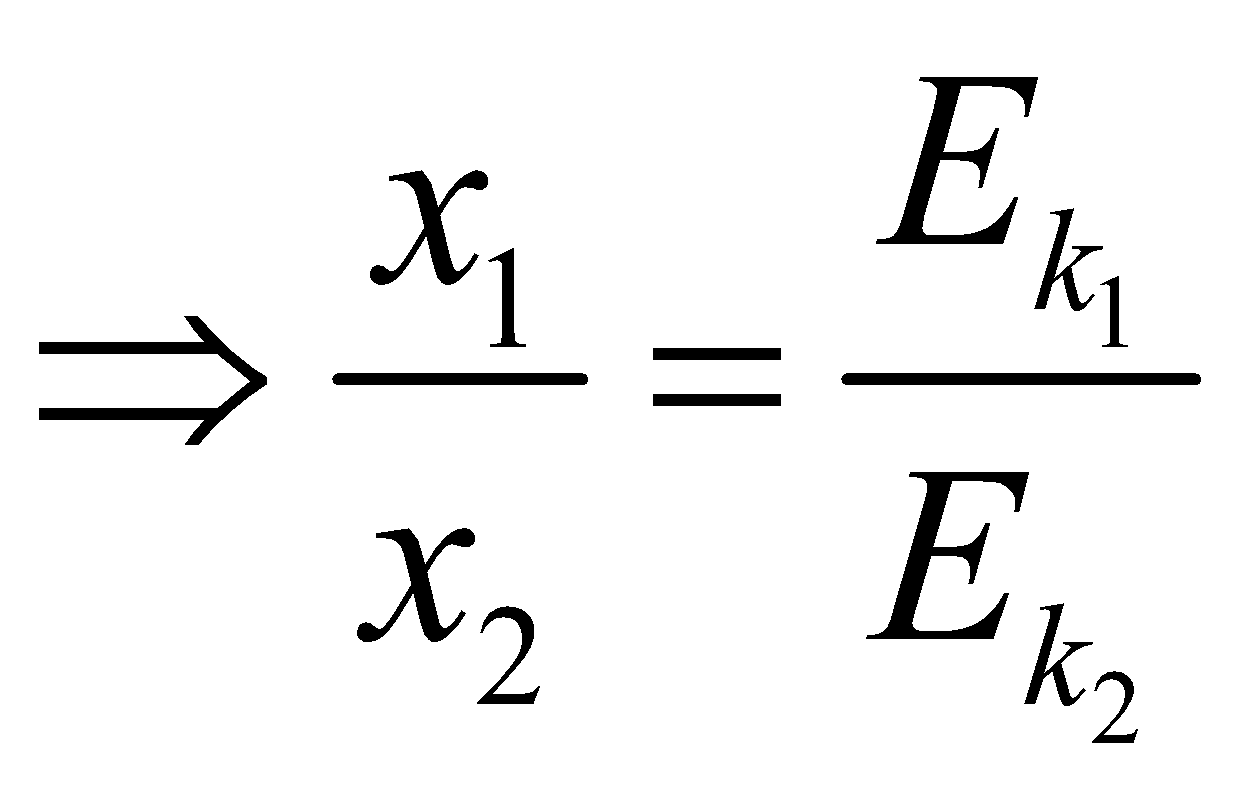 ….(ii)
Let us apply a retarding force F on M1 & M2, a1 & a2 are the decelerations of M1 & M2 respectively. Then from third equation of motion :
….(iii a)
and ….(iii b )
If t1 & t2 are the stopping time of vehicles of masses
M1 & M2 respectively, then from first equation of motion (v = u+at)
 ….(iv a)
and  ….(iv b)  
Then by rearranging equation (i), (iii) & (iv), we get
  1. If
  2. If
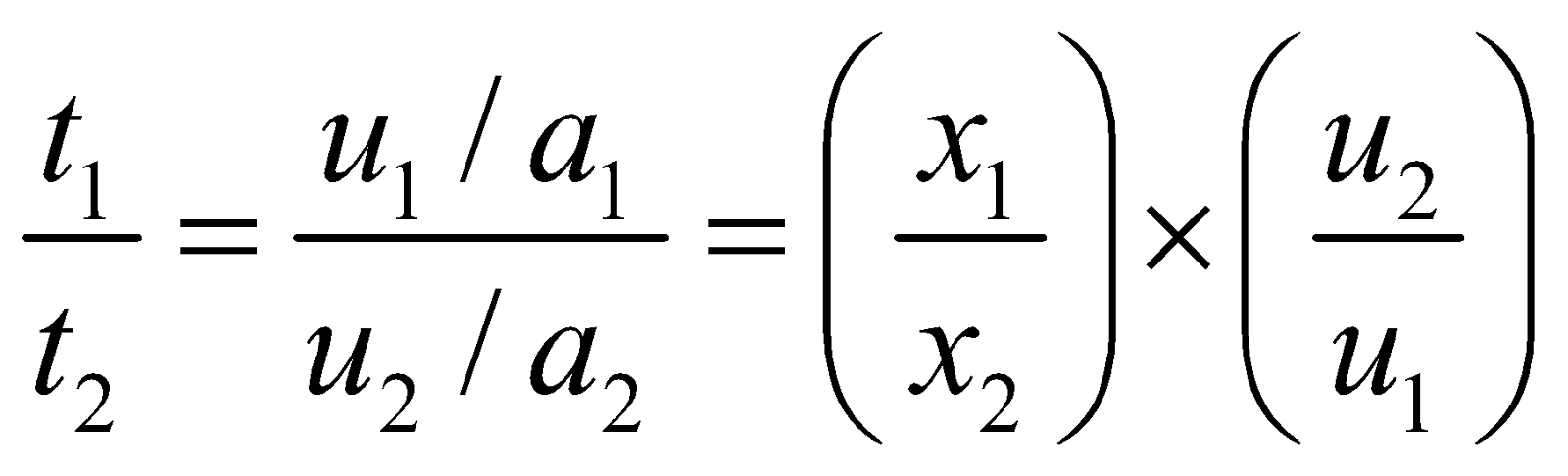
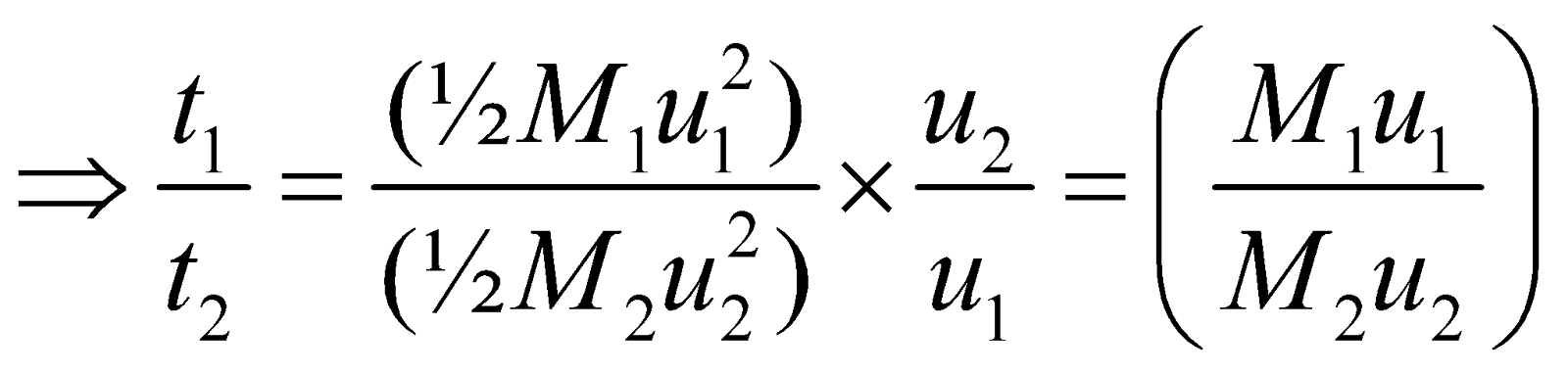
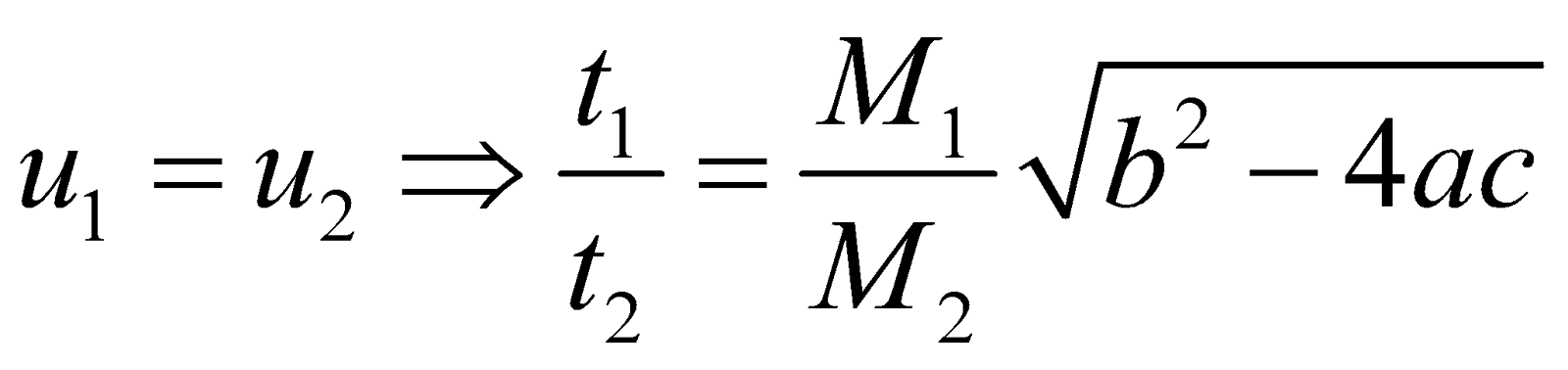
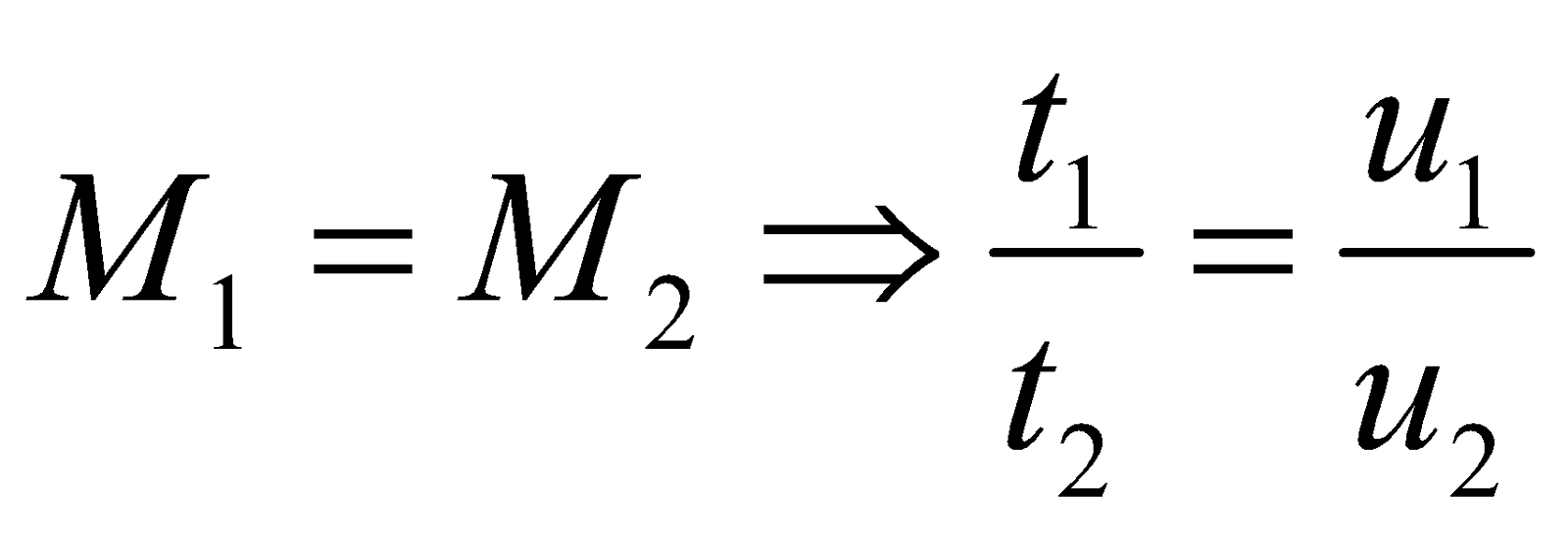
  3. If M1u1 = M2u1 ⇒ t1 = t2 and  
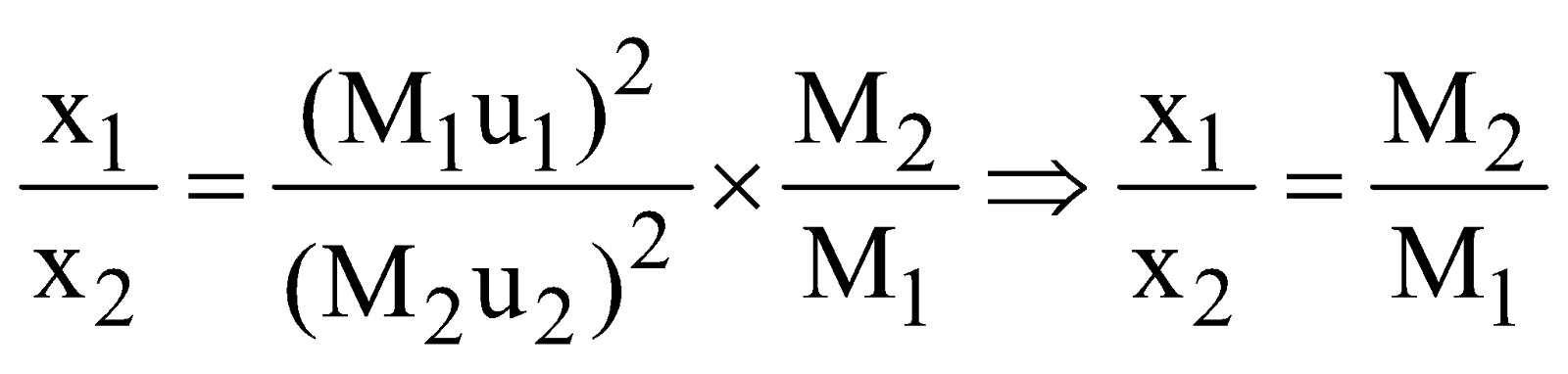
  4. Consider two vehicles of masses M1 & M2 respectively.
If they are moving with same velocities, then the ratio of their stopping distances by the application of same retarding force is given by
and let M2 > M1 then x1 < x2
lighter mass will cover less distance then the heavier mass
And the ratio of their retarding times are as follows :  
i.e  
  1. If kinetic energy of a body is doubled, then its momentum becomes 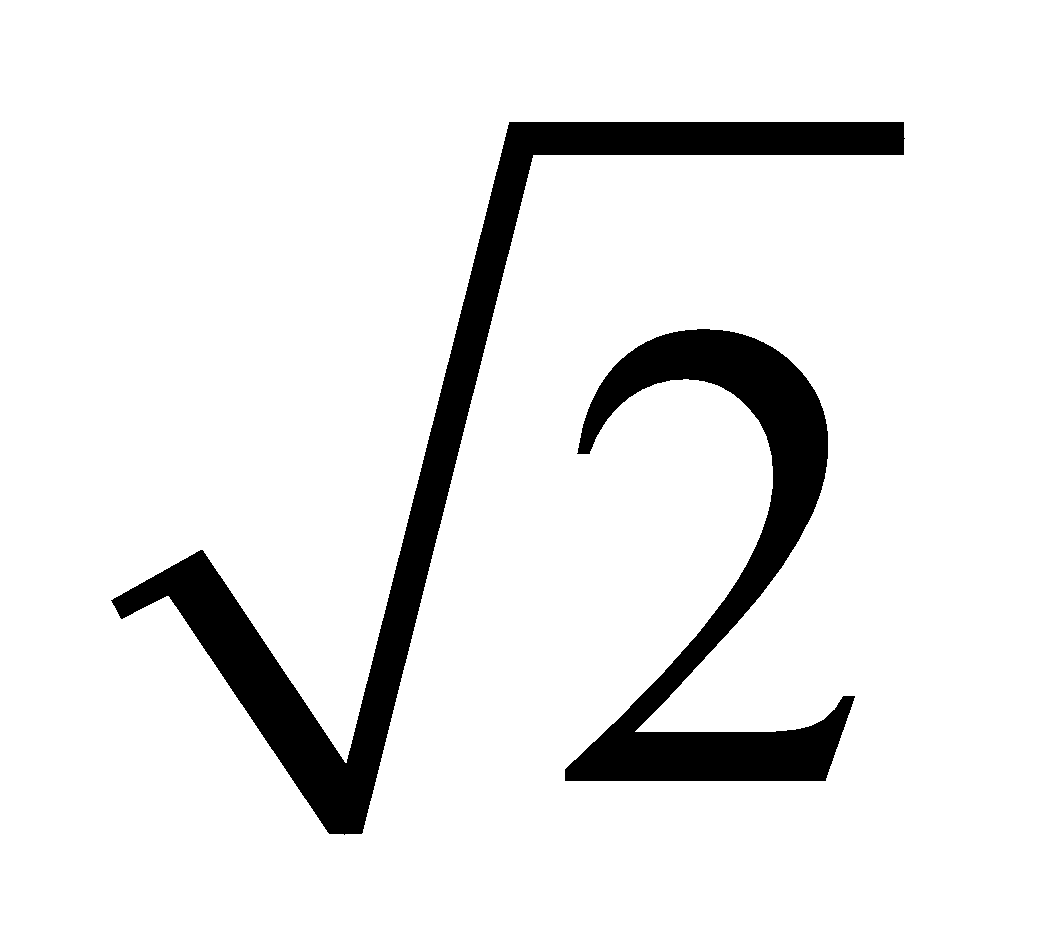times,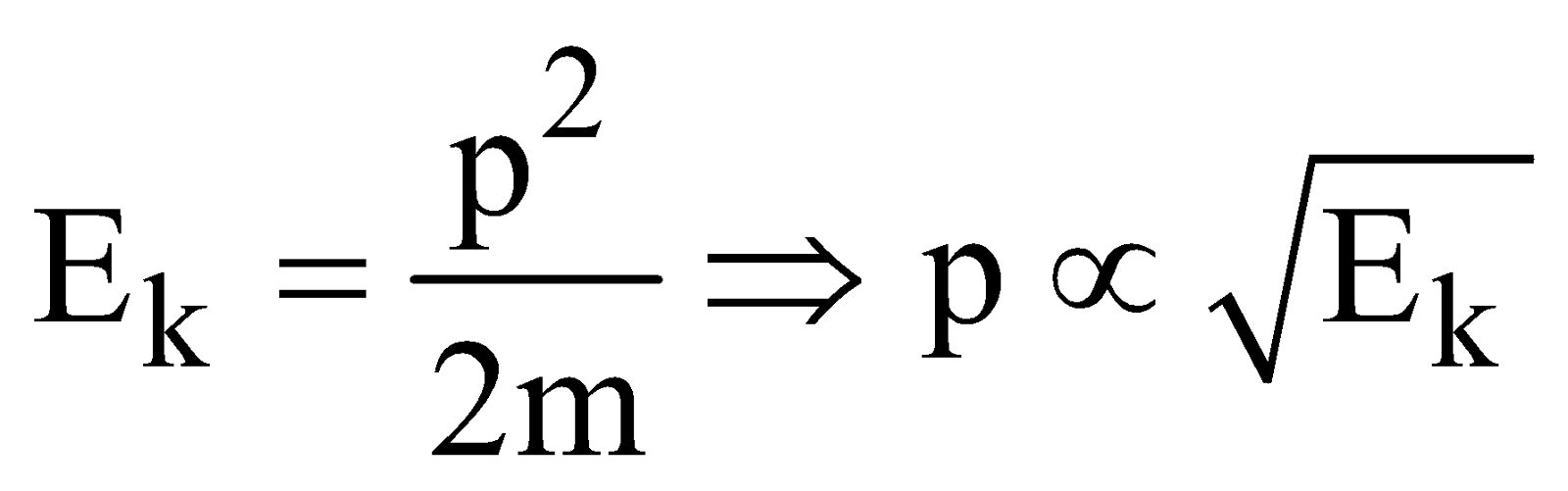
  2. If two bodies of masses m1 and m2 have equal kinetic energies, then their velocities are inversely proportional to the square root of the respective masses. i.e.
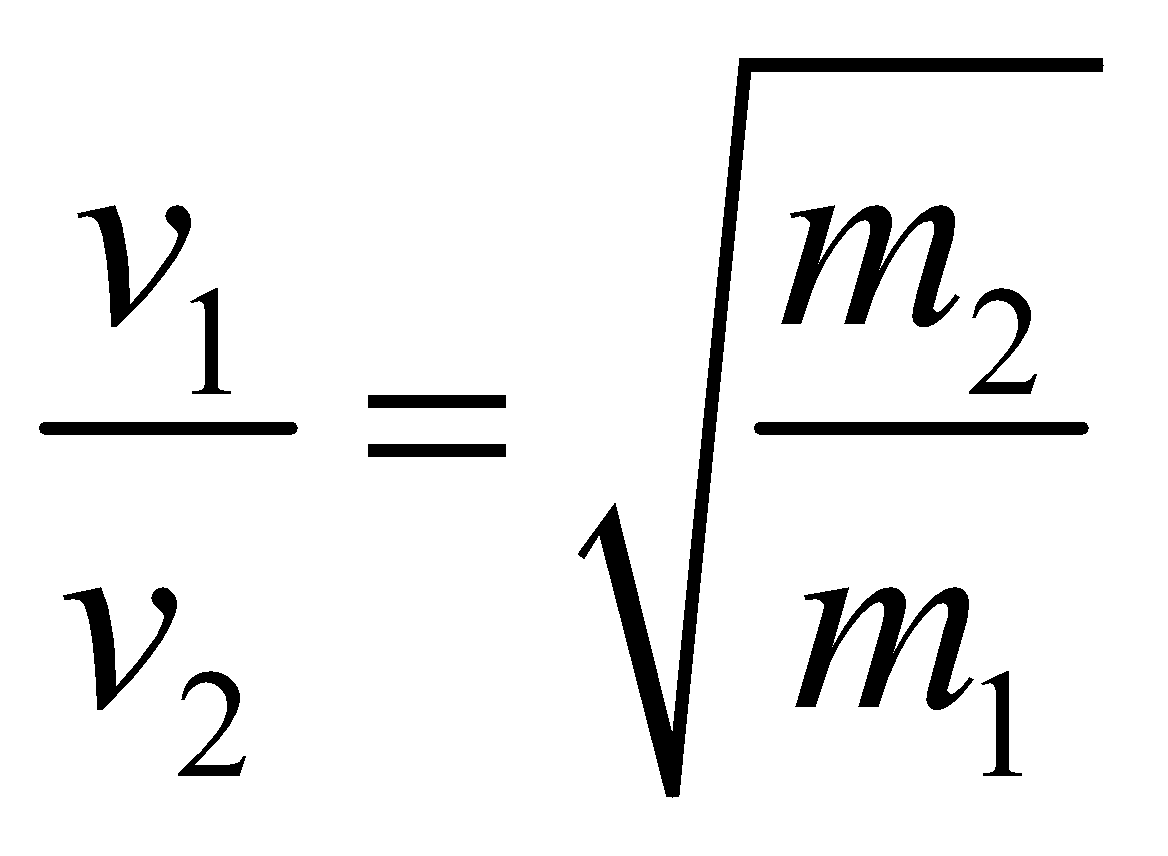
  1. The spring constant of a spring is inversely proportional to the no. of turns i.e.  
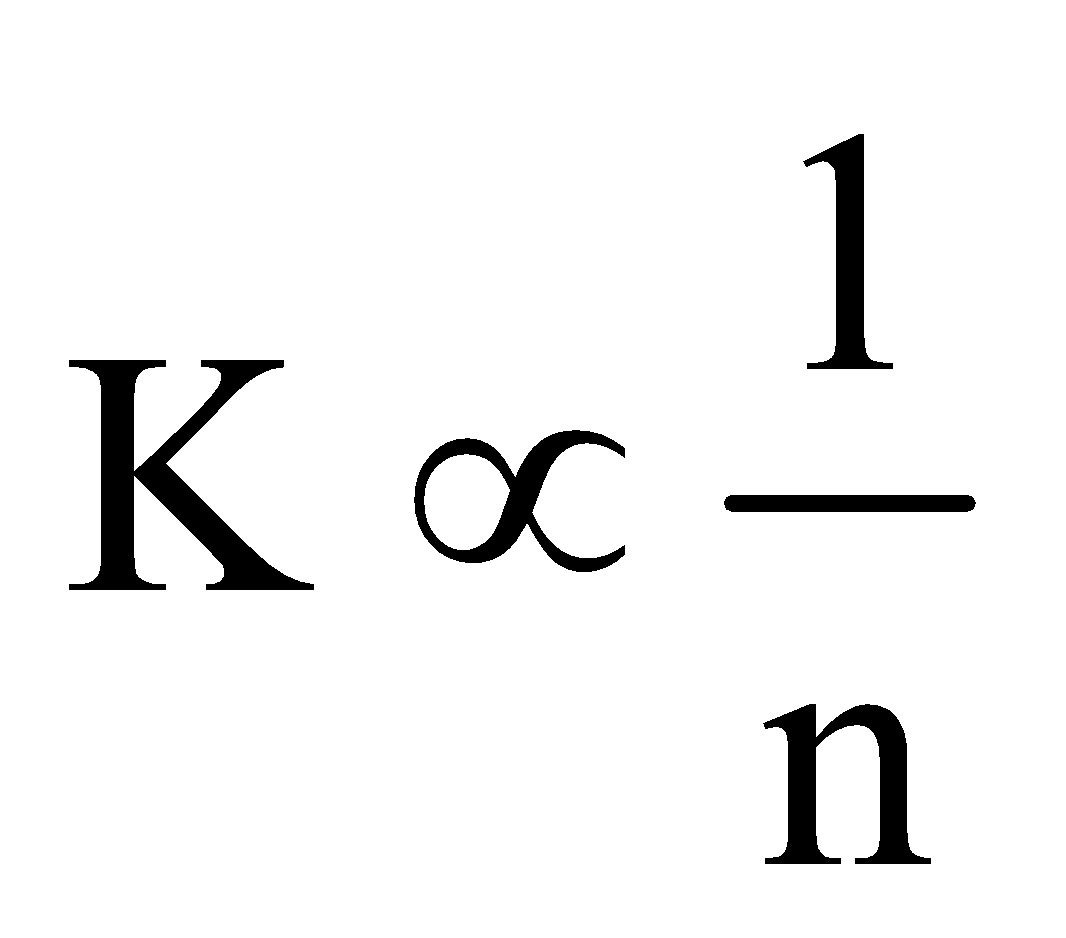     or kn = const.
Greater the no. of turns in a spring, greater will be the work done i.e. W ∝ n
The greater is the elasticity of the spring, the greater is the spring constant.
  1. Spring constant : The spring constant of  a spring is inversely proportional to length i.e., 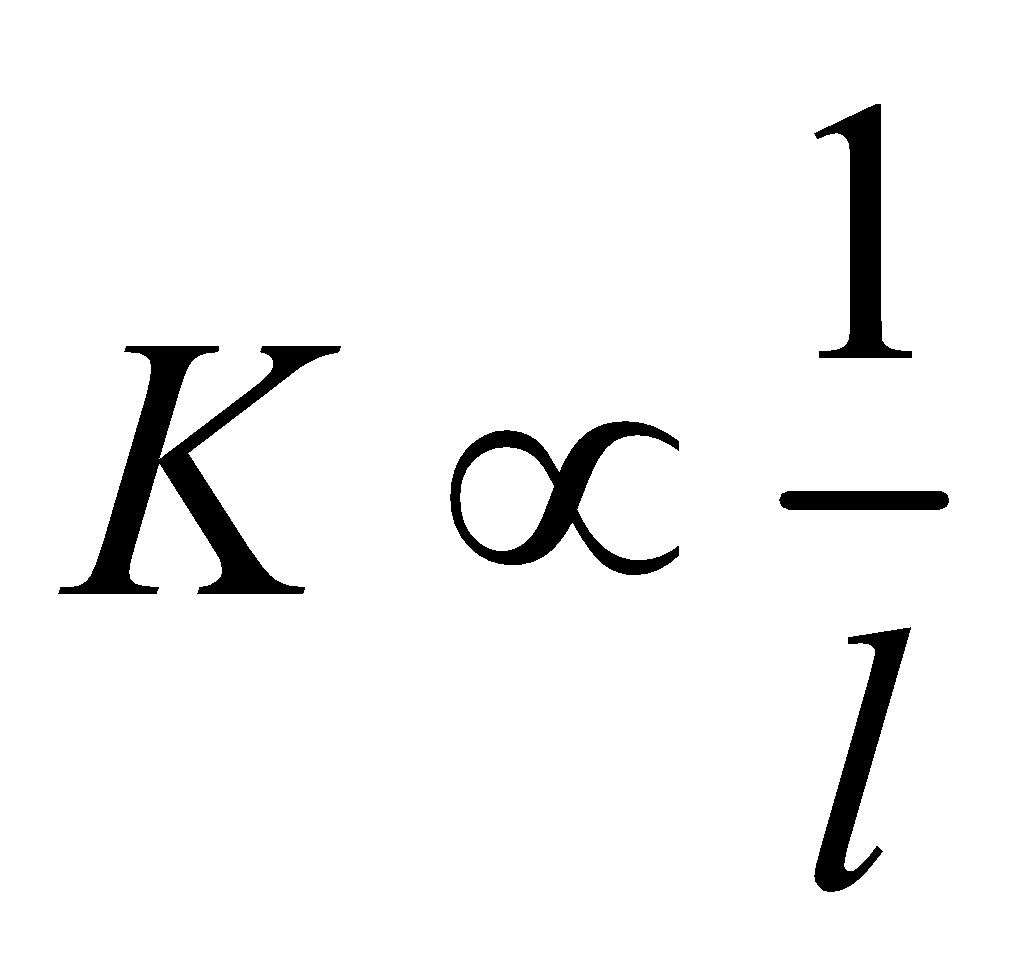or Kl = constant.
    1. If a spring is divided into n equal parts, the spring constant of each part = nK.
    2. If spring of spring constant K1, K2, K3 ………. are connected in series, then effective force constant
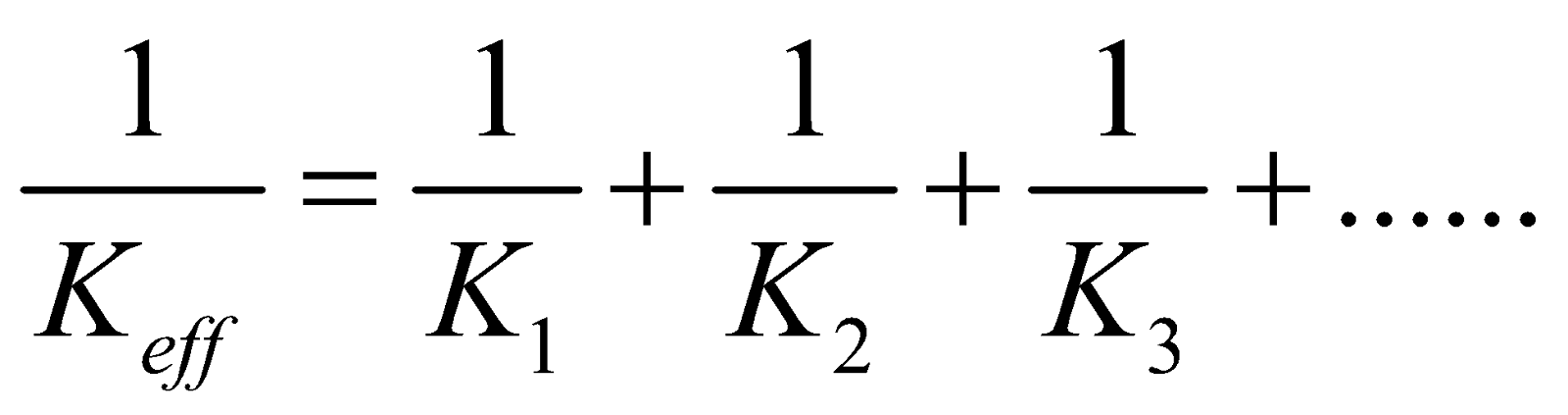
    3. If spring of spring constant K1, K2, K3……….. are connected in parallel, then effective spring constant  
      Keff  = K1 + K2 + K3 +………….

 

Scroll to Top