- IB DP Physics 2025 SL- IB Style Practice Questions with Answer-Topic Wise-Paper 1
- IB DP Physics 2025 HL- IB Style Practice Questions with Answer-Topic Wise-Paper 1
- IB DP Physics 2025 SL- IB Style Practice Questions with Answer-Topic Wise-Paper 2
- IB DP Physics 2025 HL- IB Style Practice Questions with Answer-Topic Wise-Paper 2
Learning Objectives
Students should understand:
• the principle of the conservation of energy
• that work done by a force is equivalent to a transfer of energy
• that energy transfers can be represented on a Sankey diagram
• that work W done on a body by a constant force depends on the component of the force along the line of displacement s is given by W = Fs cos θ
• that work done by the resultant force on a system is equal to the change in the energy of the system
• that mechanical energy is the sum of kinetic energy, gravitational potential energy and elastic potential energy
• that in the absence of frictional, resistive forces, the total mechanical energy of a system is conserved
• that if mechanical energy is conserved, work is the amount of energy transformed between different forms of mechanical energy in a system, such as:
◦ the kinetic energy of translational motion as given by \(E_k=\frac{1}{2}mv^2 =\frac{p^2}{2m}\)
◦ the gravitational potential energy, when close to the surface of the Earth as given by ΔEp = mgΔh
◦ the elastic potential energy as given by \(E_H=\frac{1}{2}k(\Delta x)^2\)
• that power developed P is the rate of work done, or the rate of energy transfer, as given by \(p=\frac{\Delta W}{\Delta t}=Fv\)
• efficiency η in terms of energy transfer or power as given by \(\eta=\frac{E_{output}}{E_{input}}=\frac{P_{output}}{P_{input}}\)
• energy density of the fuel sources.
Efficiency
Sankey Diagram Rules: Width of the arrow proportional to the amount of energy | 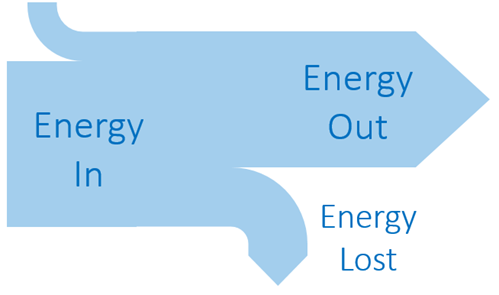 |
Sankey Diagram
Energy sources go through several processes before it becomes the useful energy we use and we can provide a visual representation of this through Sankey diagram. , Sankey diagram is a visual representation of the flow of the energy in a device or in a process.
When drawing a Sankey diagram, there are some rules to remember:
- Each energy source and loss in the process is represented by an arrow.
- The diagram is drawn to scale with the width of an arrow being proportional to the amount of energy it represents.
- The energy flow is drawn from left to right.
- When energy is lost from the system it moves to the top or bottom of the diagram.
- Power transfers as well as energy flows can be represented.
If we flow these rules, then we can come up with a Sankey diagram for a lamp.

From the Sankey diagram, we can notice that large portion of the total energy is leaked through power generation and internal energy of light bulb. Any energy that is leaked and no longer useful is called degraded energy. Hence through the Sankey diagram, we can also know the efficiency of energies.
Example: Energy balance in the Earth surface–atmosphere system
Earth’s energy balance describes how the incoming energy from the sun is used and returned to space. If incoming and outgoing energy are in balance, the Earth’s temperature remains constant.
