Question
A mass is oscillating with simple harmonic motion. At time \(t\), the acceleration is a positive maximum. What are the displacement and velocity of the mass at time \(t\) ?
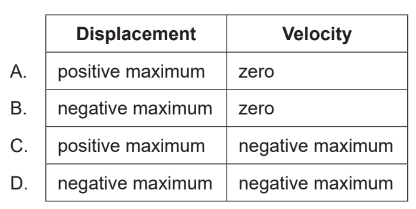
▶️Answer/Explanation
Ans:B
When a mass is undergoing simple harmonic motion, its acceleration and displacement are related to the phase of the motion. Let’s break this down:
1. In simple harmonic motion, acceleration is indeed negatively related to displacement, meaning when displacement is at its maximum positive value, acceleration is at its maximum negative value, and vice versa. So, if the acceleration is a positive maximum, the displacement will be at its maximum negative value (furthest in the opposite direction)
2. Velocity at this point: At this point, the velocity is zero. As the mass changes direction at the extreme points of its motion (maximum displacement), the velocity momentarily drops to zero before it starts moving in the opposite direction.
So, at time \(t\) when the acceleration is a positive maximum:
Displacement (\(x\)) is at its maximum negative value.
Velocity (\(v\)) is zero.
This describes the behavior of an object undergoing simple harmonic motion.
Question
Which graph shows the variation with time t of the kinetic energy (KE) of an object undergoing simple harmonic motion (shm) of period T?
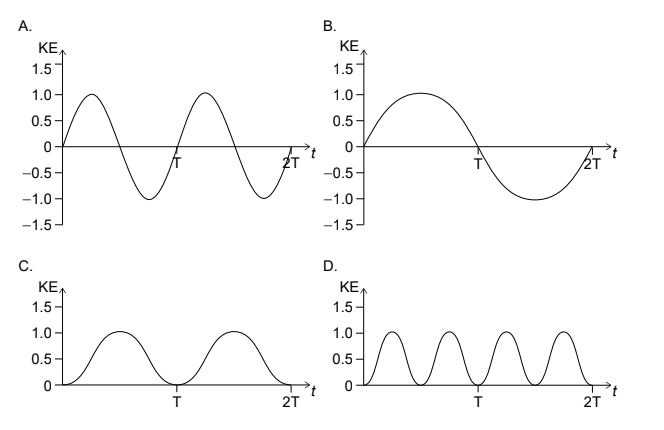
Answer/Explanation
Answer – D
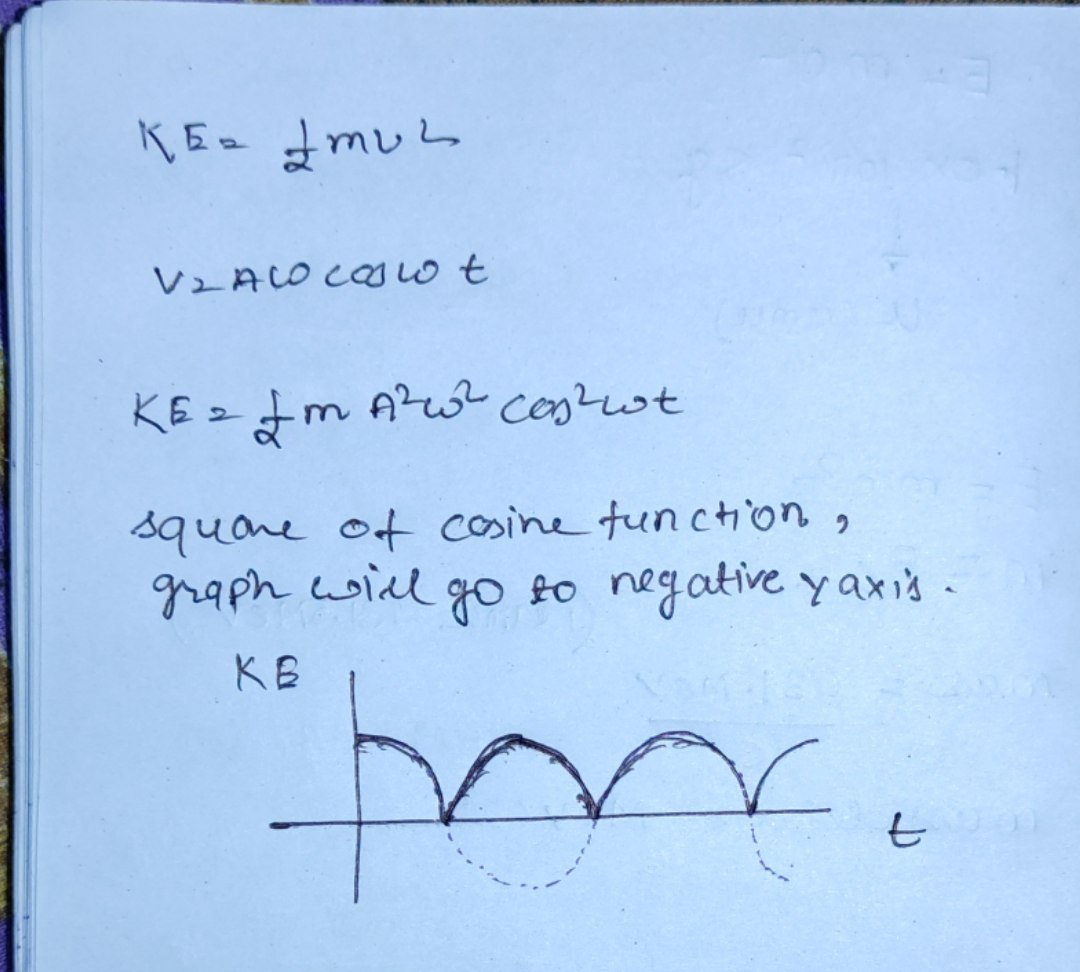
Question
A pendulum oscillating near the surface of the Earth swings with a time period T. What is the time period of the same pendulum near the surface of the planet Mercury where the gravitational field strength is 0.4g?
A. 0.4T
B. 0.6T
C. 1.6T
D. 2.5T
Answer/Explanation
Markscheme
C
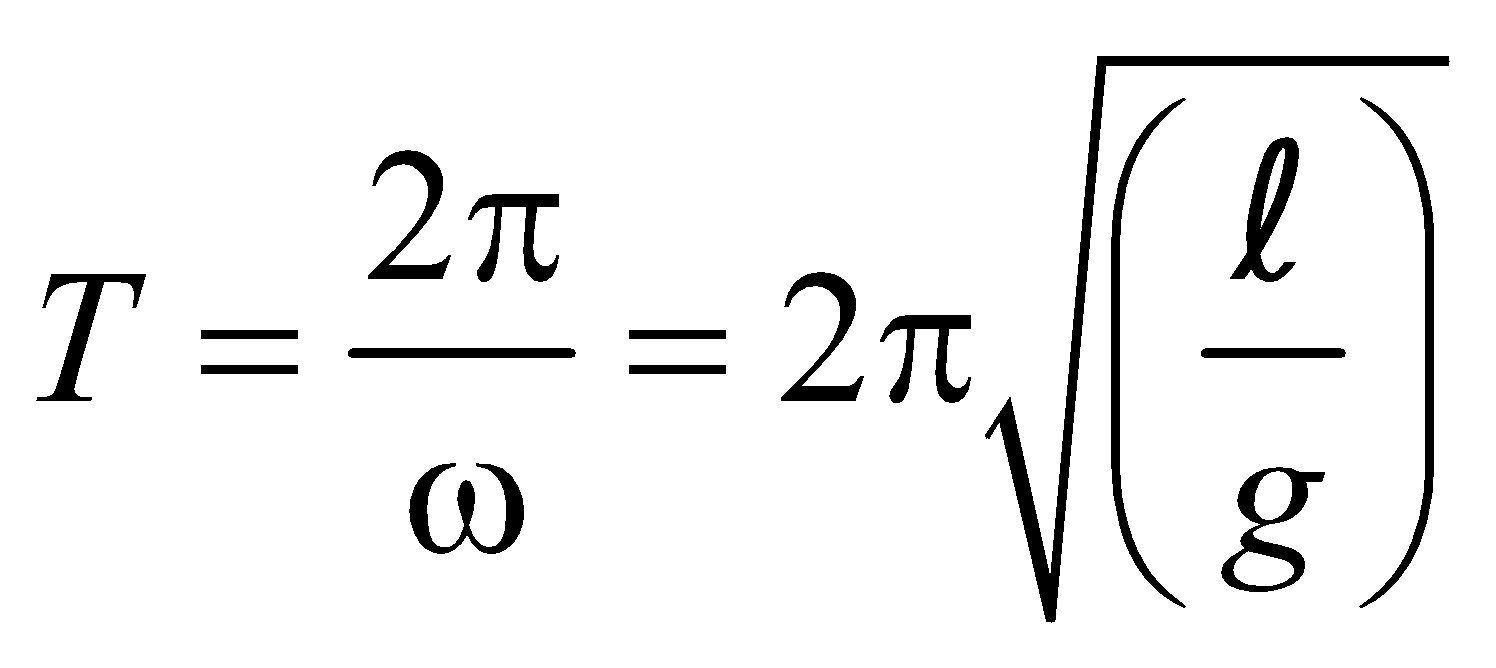
\(T_{earth}=2\pi\sqrt{\frac{l}{g_{earth}}}\)
\(T_{Merc}=2\pi\sqrt{\frac{l}{g_{Merc}}}\)
or
\(\frac{T_{Merc}}{T_{earth}}=\sqrt{\frac{g_{earth}}{g_{Merc}}}\)
\(=\sqrt{\frac{g}{0.4g}}=\sqrt{2.5}\)
\(T_{Merc}\approx 1.6T\)
Question
A mass–spring system oscillates vertically with a period of T at the surface of the Earth. The gravitational field strength at the surface of Mars is 0.3 g . What is the period of the same mass–spring system on the surface of Mars?
A. 0.09T
B 0.3T
C T
D 3T
Answer/Explanation
Answer – C
The time period of spring mass system is independent of the gravitation field .
\( T=2\pi \sqrt{\frac{m}{k}} \)

A. The angular frequency of the oscillation
B. The total energy of the mass
C. The average speed of the mass
D. The maximum kinetic energy of the mass.
Answer/Explanation
Angular frequency of a spring: The angular frequency of a spring is dependent only on the spring constant and the mass of the object.