Question
A standing wave with a first harmonic of frequency \(f_1\) is formed on a string fixed at both ends.

The frequency of the third harmonic is \(f_3\).
What is \(\frac{f_1}{f_3}\) ?
A. 3
B. \(\frac{3}{2}\)
C. \(\frac{2}{3}\)
D. \(\frac{1}{3}\)
▶️Answer/Explanation
Ans:D
In a standing wave on a string fixed at both ends, the frequencies of the harmonics are related as follows:
- The frequency of the first harmonic (\(f_1\)) is the fundamental frequency.
- The frequency of the nth harmonic is given by \(f_n = nf_1\).
So, the frequency of the third harmonic (\(f_3\)) is:
\(f_3 = 3f_1\).
Now, we can find \(\frac{f_1}{f_3}\):
\(\frac{f_1}{f_3} = \frac{f_1}{3f_1} = \frac{1}{3}\).
So, the correct answer is:
D. \(\frac{1}{3}\).
Question
A pipe containing air is closed at one end and open at the other. The third harmonic standing wave for this pipe has a frequency of \(150 \mathrm{~Hz}\).
What other frequency is possible for a standing wave in this pipe?
A. \(25 \mathrm{~Hz}\)
B. \(50 \mathrm{~Hz}\)
C. \(75 \mathrm{~Hz}\)
D. \(300 \mathrm{~Hz}\)
▶️Answer/Explanation
Ans:B
In a closed-open pipe (like an open-end organ pipe), the fundamental frequency (first harmonic) is produced when the length of the pipe is one-fourth (1/4) of the wavelength of the sound wave. In this case, the pipe is closed at one end and open at the other.
The third harmonic has a frequency of \(150 \, \text{Hz}\), which means that the pipe length corresponds to one and a half wavelengths (\(\lambda/2\)). The fundamental frequency (\(f_1\)) corresponds to a quarter-wavelength (\(\lambda/4\)).
So, if the third harmonic is at \(150 \, \text{Hz}\), we can find the fundamental frequency (\(f_1\)) as follows:
\(\frac{f_3}{f_1} = \frac{\lambda_3}{\lambda_1} = \frac{3}{1}\)
\(f_1 = \frac{f_3}{3} = \frac{150 \, \text{Hz}}{3} = 50 \, \text{Hz}\)
Therefore, the possible frequency for a standing wave in this pipe, other than the third harmonic, is the fundamental frequency, which is \(50 \, \text{Hz\).
Question
The frequency of the first harmonic standing wave in a pipe that is open at both ends is 200 Hz. What is the frequency of the first harmonic in a pipe of the same length that is open at one end and closed at the other?
A. 50 Hz
B. 75 Hz
C. 100 Hz
D. 400 Hz
Answer/Explanation
Markscheme
C
For Pipe Open at both Ends
\(L=n{}’\frac{\lambda}{2}\)
\(v= f \lambda\)
or
\(f=\frac{v}{\lambda}=\frac{n{}’}{2L} \times v\)
For first harmonic \(n{}’ =1 \)
\(f_{1(n=1)}=\frac{1}{2L}v =200\; Hz\) —-(1)
For Pipe closed at one end
\(L=(2n+1)\frac{\;\lambda}{4} \; where \; n=0,1,2,3 \; etc..\)
\(\because v=f\lambda\)
\(\therefore f=\frac{v}{\lambda}=\frac{2n+1}{4L}\times v\)
\(f_{2(n=0)}=\frac{1}{4L}v\) —-(2)
From eqn (1) and (2) We get
\(f_{2(n=0)} =100\; Hz\)
Question
The air in a pipe, open at both ends, vibrates in the second harmonic mode.
![]()
P Q
![]()
What is the phase difference between the motion of a particle at P and the motion of a particle at Q?
A 0
B
C π
D 2π
Answer/Explanation
Answer – C
For an open organ pipe, the length L is given as
\(L=n\frac{\Lambda }{2}\)
where, λ is the wavelength of wave and n is an integer and by putting n = 1,2,3,…………… we get the modes of vibration.
n=1 gives first harmonics, n=2 gives second harmonics and so on.
Here, an open organ pipe of length L vibrates in second harmonic mode,
hence the length of pipe is
\(L=\frac{2\Lambda }{2}=\Lambda\)
\(L=\Lambda\)
And P and Q at \(\frac{\Lambda }{2}\)
Phase difference \(=\frac{2\pi }{\Lambda }\left ( \Delta x \right )\) path difference.
Which is equal to \(\pi \)
Two pulses are travelling towards each other.

What is a possible pulse shape when the pulses overlap?
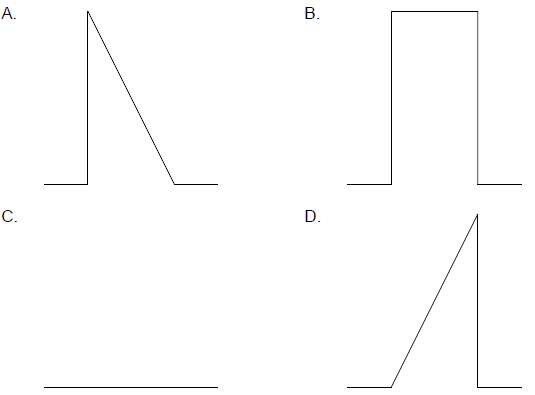
Answer/Explanation
Markscheme
A
