Question 1
Given
- A circle with centre O and radius 4cm
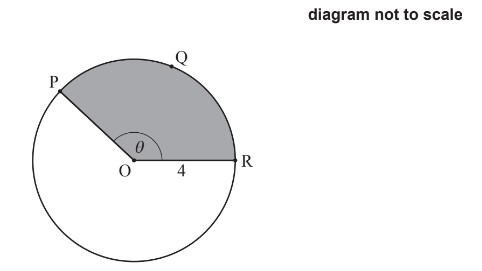
2. P, Q and R lie on the circumference of the circle and PÔR = θ, where θ is measured in radians
3. The length of arc PQR is 10 cm.
Find
- Perimeter of sector PQRO
- Angle θ
- area of the shaded sector
▶️Answer/Explanation
Answer:
(a) attempts to find perimeter
arc+2 radius × OR 10 + 4 + 4
=18 (cm)
Perimeter of sector PQRO:
The perimeter of the sector is the sum of the lengths of the arc PQR and the two radii OP and OR.
Perimeter = Arc Length + 2 * Radius
Given that the arc length of PQR is 10 cm and the radius is 4 cm,
Perimeter = 10 cm + 2 * 4 cm Perimeter = 10 cm + 8 cm Perimeter: 18 cm
So, the perimeter of sector PQRO is 18 cm.
(b) 10 = 4 θ
θ = \(\frac{10}{4}\) (=\(\frac{5}{2}\), 2.5 )
Angle θ:
The angle in radians is related to the arc length and the radius by the formula:
θ = Arc Length / Radius
Given that the arc length of PQR is 10 cm and the radius is 4 cm,
θ = \(\frac{10}{4}\) =\(\frac{5}{2}\)= 2.5
θ = 2.5 radians
So, the angle θ is 2.5 radians.
(c) area = \(\frac{1}{2}\) ( = \(\frac{10}{4}\) \((4^2\)) (=1.25 × 16)
= 20 \((cm^2\))
Area of the shaded sector:
The area of the sector is given by the formula:
Area = =\(\left ( \frac{\theta }{2}\right )r^{2}\)
Where θ is the angle in radians and r is the radius.
Given that θ is 2.5 radians and the radius is 4 cm:
Area =\(\left ( \frac{2.5}{2}\right )4^{2}\)
Area = 1.25 * 16 cm² Area = 20 cm²
So, the area of the shaded sector is 20 square centimeters.
Question 2
Part A
Given
- arithmetic sequence with \(u_1\) = 0.6 and \(u_4\) = 0.15
Find
- common difference, d
Part B:
Given
probability distribution of a discrete random variable X such that P(X=n) = \(\frac{u_n}{k}\), where \(n\epsilon \mathbb{Z}^+\), 1 ≤ n ≤ 4 and \(k\epsilon \mathbb{R}^+\)
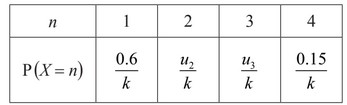
Find
b. Find the value of k .
▶️Answer/Explanation
Answer:
(a) \(u_1 + 3d = u_4\)
0.6 + 3d = 0.15
d = -0.15
In an arithmetic sequence, the nth term (denoted as \(u_{n}\) is given by the formula:
\(u_{n}=u_{1}+\left ( n-1 \right )d\)
In this case, you are given \(u_{1}=0.6\)and \(u_{4}=0.15\) Let’s use this information to find the common difference d.
For\(u_{4}\)
\(u_{4}=u_{1}+\left ( 4-1 \right )d\)
\(0.15=0.6+3d\)
Now, solve for d:
\(3d=0.15-0.6\Rightarrow 3d=-0.45\)
Divide both sides by 3 to find d=-0.15
So, the common difference (d) is -0.15 in this arithmetic sequence.
(b) METHOD 1
\(u_2 = 0.45\) or \(u_3 = 0.3\) (may be seen in their equation)
summing their probabilities to 1 (seen anywhere)
\(\frac{0.6}{k}+\frac{u_2}{k}+\frac{u_3}{k}+\frac{0.15}{k}=1\)
\(\frac{0.6}{k}+\frac{0.45}{k}+\frac{0.3}{k}+\frac{0.15}{k}=1\) (or equivalent)
\(\frac{1.5}{k} = 1\)
k = 1.5
METHOD 2 (using \(S_n\) formula)
\(S_4 = \frac{4}{2}(2(0.6)+(4-1)(-0.15))\) OR \(S_4=\frac{4}{2}(2(\frac{0.6}{k})+(4-1)(\frac{-0.15}{k}))\)
OR \(S_4 = \frac{4}{2}(0.6 + 0.15)\) OR \(S_4 = \frac{4}{2}(\frac{0.6}{k}+\frac{0.15}{k})\) (or equivalent)
summing their probabilities to 1 (seen anywhere)
\(\frac{u_1}{k} \frac{u_2}{k} \frac{u_3}{k} \frac{u_4}{k}\) OR \(u_1+u_2+u_3+u_4 = k\) OR \(S_4\) = 1 OR \(S_4\) = k
\(\frac{4}{2}\) (2(0.6)+(4-1)(-0.15)) = k (or equivalent)
k = 1.5
To find the value of k, you need to use the fact that the sum of probabilities in any probability distribution should equal 1.
The probability distribution given is: \(P(X=n)=\frac{u_{n}}{k}\),n=1,2,3,4
\(P(X=1)=\frac{u_{1}}{k}\)
\(P(X=2)=\frac{u_{2}}{k}\)
\(P(X=3)=\frac{u_{3}}{k}\)
\(P(X=4)=\frac{u_{4}}{k}\)
Since the sum of probabilities should be 1, we have:
P(X=1)+P(X=2)+P(X=3)+P(X=4)=1
\(\frac{u_{1}}{k}+\frac{u_{2}}{k}+\frac{u_{3}}{k}+\frac{u_{4}}{k}=1\)…………….(1)
Given in Part (a) \(u_{1}=0.6\), \(u_{4}=0.15\) and d=-0.15
With the help of an arithmetic sequence, the nth term formula \(u_{n}=u_{1}+\left ( n-1 \right )d\) we can find \(u_{2} and u_{3}\)
\(u_{2}=0.6+\left ( 2-1 \right )(-0.15)\Rightarrow 0.45\)
\(u_{3}=0.6+\left ( 3-1 \right )(-0.15)\Rightarrow 0.3\)
Plug in all the values in equation (1)
\(\frac{0.6}{k}+\frac{0.45}{k}+\frac{0.3}{k}+\frac{0.15}{k}=1\)
Combine the terms:
\(\frac{1.5}{k}=1\)
Now, solve for k:
k=1.5
