IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 2.2 – Forces
Topic 2 Weightage : 13 %
All Questions for Topic 2.2 – Objects as point particles , Free-body diagrams , Translational equilibrium , Newton’s laws of motion ,Solid friction
Question
The magnitude of the resultant of two forces acting on a body is 12N. Which pair of forces acting on the body can combine to produce this resultant?
A. 1N and 2N
B. 1N and 14N
C. 5N and 6N
D. 6N and 7N
▶️Answer/Explanation
Ans:
#
If A and B are two vectors then of these will vary from
to
and
»
,
and
»
,
and
»
,
and
»
,
Hence will get from
and
Question
Two identical boxes are stored in a warehouse as shown in the diagram. Two forces acting on the top box and two forces acting on the bottom box are shown.
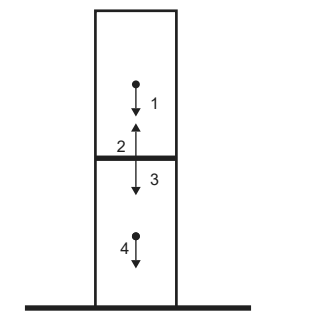
Which is a force pair according to Newton’s third law?
A 1 and 2
B 3 and 4
C 2 and 3
D 2 and 4
▶️Answer/Explanation
Ans: C
For every action, there is an equal and opposite reaction.
The statement means that in every interaction, there is a pair of forces acting on the two interacting objects. The size of the forces on the first object equals the size of the force on the second object. The direction of the force on the first object is opposite to the direction of the force on the second object. Forces always come in pairs – equal and opposite action-reaction force pairs.
This is contact or Normal force , which act in pair according to Newton’s Third Law of motion.
Ref: https://www.iitianacademy.com/ib-physics-unit-2-mechanics-forces-dynamics-notes/
NORMAL FORCE
Question
Two forces act on an object in different directions. The magnitudes of the forces are 18 N and 27 N. The mass of the object is 9.0 kg. What is a possible value for the acceleration of the object?
A 0 m 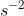
B. 0.5 m 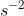
C. 2.0 m 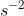
D. 6.0 m 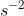
▶️Answer/Explanation
Ans: C
Let us find the range of acceleration to see which option is best fitted.
Maximum acceleration is when both forces are in same direction.
Net force = 18 N +27 n = 45 N, Hence \(a=\frac{F}{m} = \frac{45}{9}= 5 ms^{-2}\)
Minimum Force is when both forces are in opposite direction
Net Force = 27 N – 18 N = 9 N , Hence \(a=\frac{F}{m} = \frac{9}{9}= 1\; ms^{-2}\). All other result will be in between these two depends on the angle between these two forces.
Hence Suitable option for the question is C
Question
Which statement applies to an object in translational equilibrium?
A. The object must be stationary.
B. The object must be moving with constant acceleration.
C. The resultant force acting on the object must be zero.
D. There must be no external forces acting on the object.
▶️Answer/Explanation
Markscheme
C
Ref: https://www.iitianacademy.com/ib-physics-unit-2-mechanics-forces-dynamics-notes/
An object is said to be in equilibrium when there is no external net force acting on it. When an object is in equilibrium, it does not accelerate. If it had a velocity, the velocity remains constant; if it was at rest, it remains at rest.
If all the forces acting on a particular object add up to zero and have no resultant force, then it’s in translational equilibrium. Examples would be a book resting on a bookshelf, or someone walking at a steady, constant speed.
An object that’s not rotating or doing so at a steady speed, the sum of the torques acting on it equaling zero, is at rotational equilibrium. Some examples of this are a Ferris wheel turning at a constant velocity, two children of equal weight balanced on either side of a seesaw, or the Earth rotating on its axis at a steady speed
Question
A constant horizontal force F is applied to a block Y. Block Y is in contact with a separate block X.
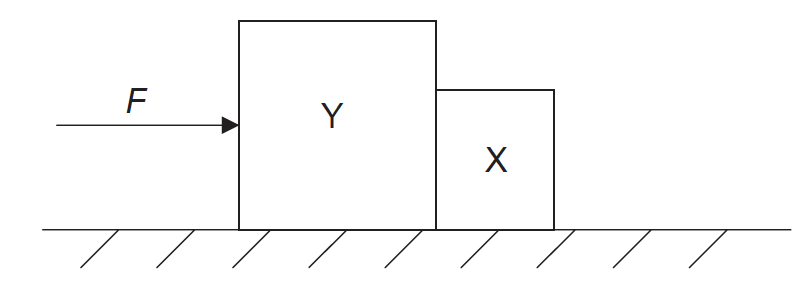
The blocks remain in contact as they accelerate along a horizontal frictionless surface. Y has a greater mass than X. Air resistance is negligible.
Which statement is correct?
A. The force F is equal to the product of the mass of Y and the acceleration of Y.
B. The force that Y exerts on X is less than F.
C. The force that Y exerts on X is less than the force that X exerts on Y.
D. The force that Y exerts on X is equal to F.
▶️Answer/Explanation
Markscheme
B
Question
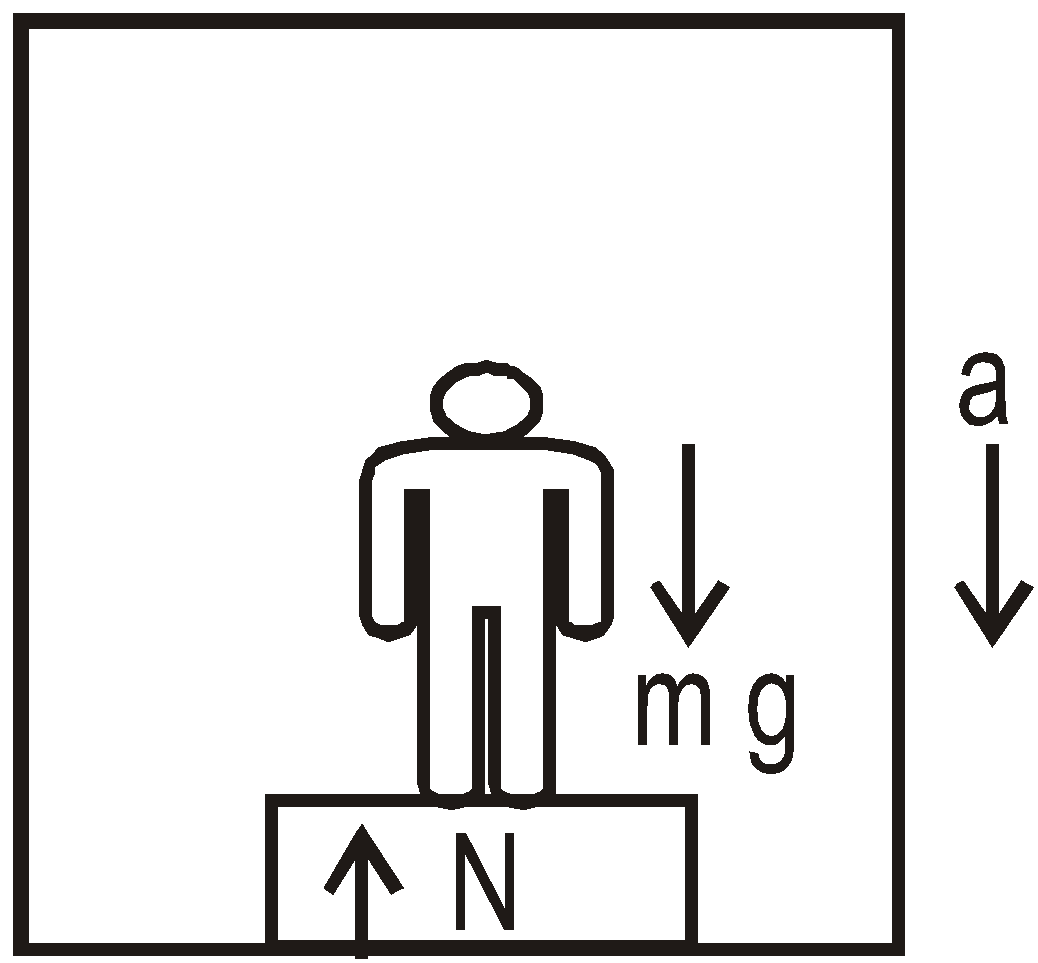
A student of mass m is in an elevator which is accelerating downwards at an acceleration a.
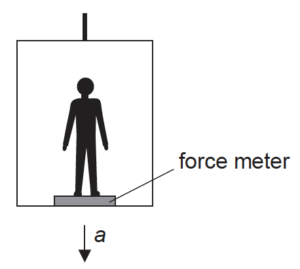
What is the reading on the force meter?
A. mg
B. mg − ma
C. mg + ma
D. ma − mg
▶️Answer/Explanation
Markscheme
B
Question
The graph shows how the net force F that acts on a body varies with the distance x that the body has travelled.
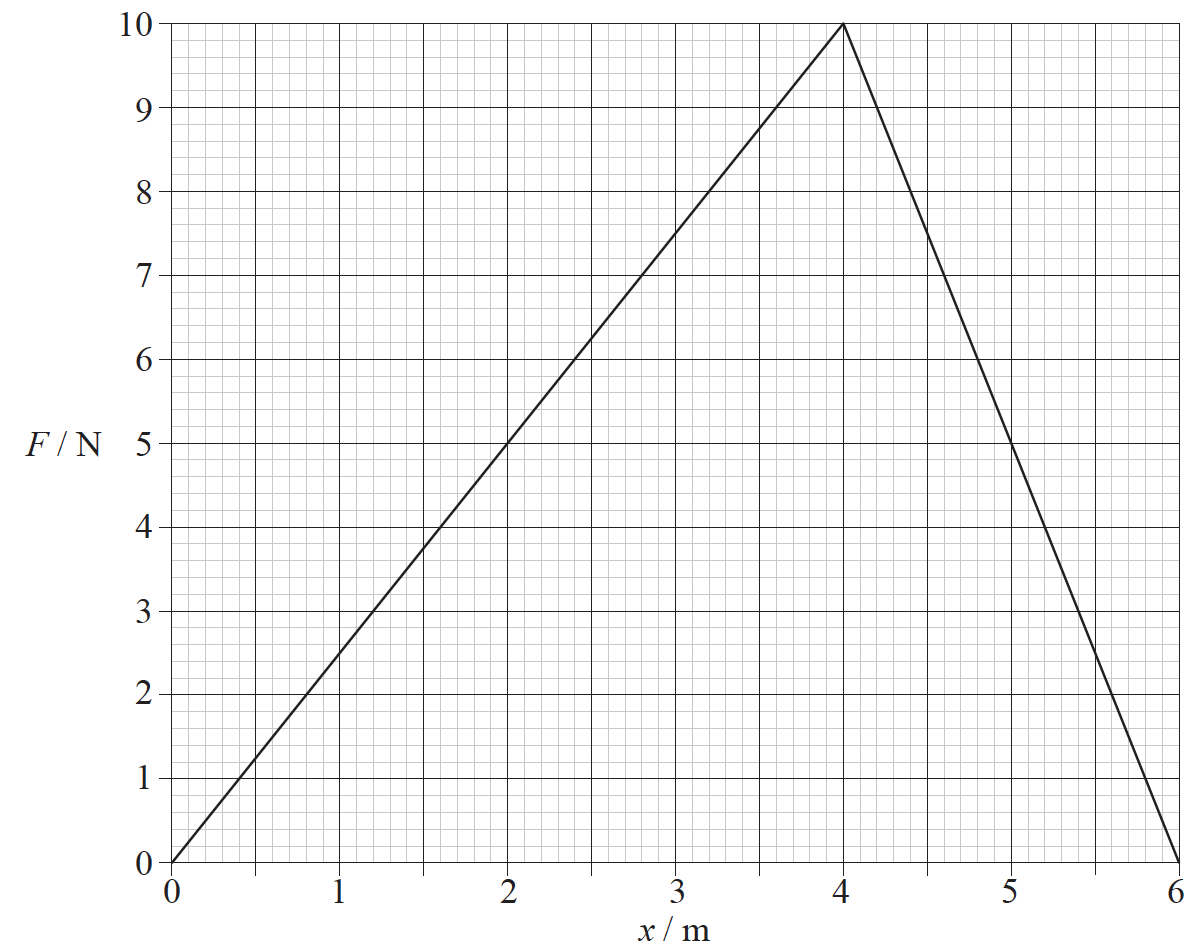
After travelling 6 m, the change in the kinetic energy of the body is
A. 0 J.
B. 20 J.
C. 30 J.
D. 60 J.
▶️Answer/Explanation
Markscheme
C
Ref: https://www.iitianacademy.com/ib-physics-unit-2-work-energy-and-power-notes/
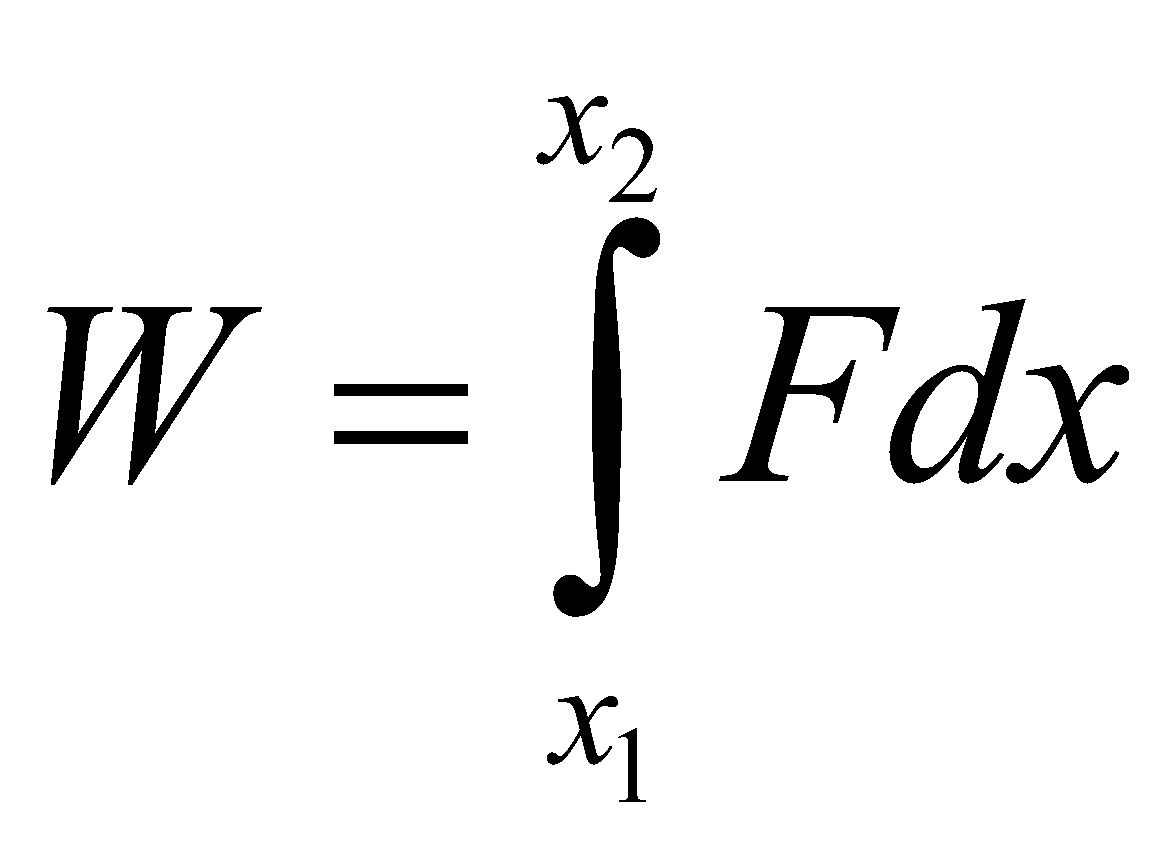 = area under force displacement graph
= area under force displacement graph