2.3 Work, energy and power
Essential Idea:
The fundamental concept of energy lays the basis upon which much of science is built
Understandings:
- Kinetic energy
- Gravitational potential energy
- Elastic potential energy
- Work done as energy transfer
- Power as rate of energy transfer
- Principle of conservation of energy
- Efficiency
Applications and Skills:
- Discussing the conservation of total energy within energy transformations
- Sketching and interpreting force–distance graphs
- Determining work done including cases where a resistive force acts
- Solving problems involving power
- Quantitatively describing efficiency in energy transfers
Principle of conservation of energy
“Energy is never created or destroyed, only transformed (e.g. into mass E = mc²), dissipated or transferred.” Energy is measured in J (joules) – energy required to move 1 N through 1m.
∆Esystem + ∆Esurroundings = 0
The energy of system changes as a result of interactions with the surroundings.
Work done (W) by a force
“The work done by a force is: force x distance moved in direction of the force”
W = Fs cos θ
The work done by a centripetal force is equal to zero, since the force is always at right angles to movement.
Graph: Work is also the area under a Force-Distance graph.
Energy (When work is done, energy is transferred)
Kinetic energy (Ek): energy related to motion – Ek = 1/2mv2
Fractional change is the change of Ek divided by the original Ek.
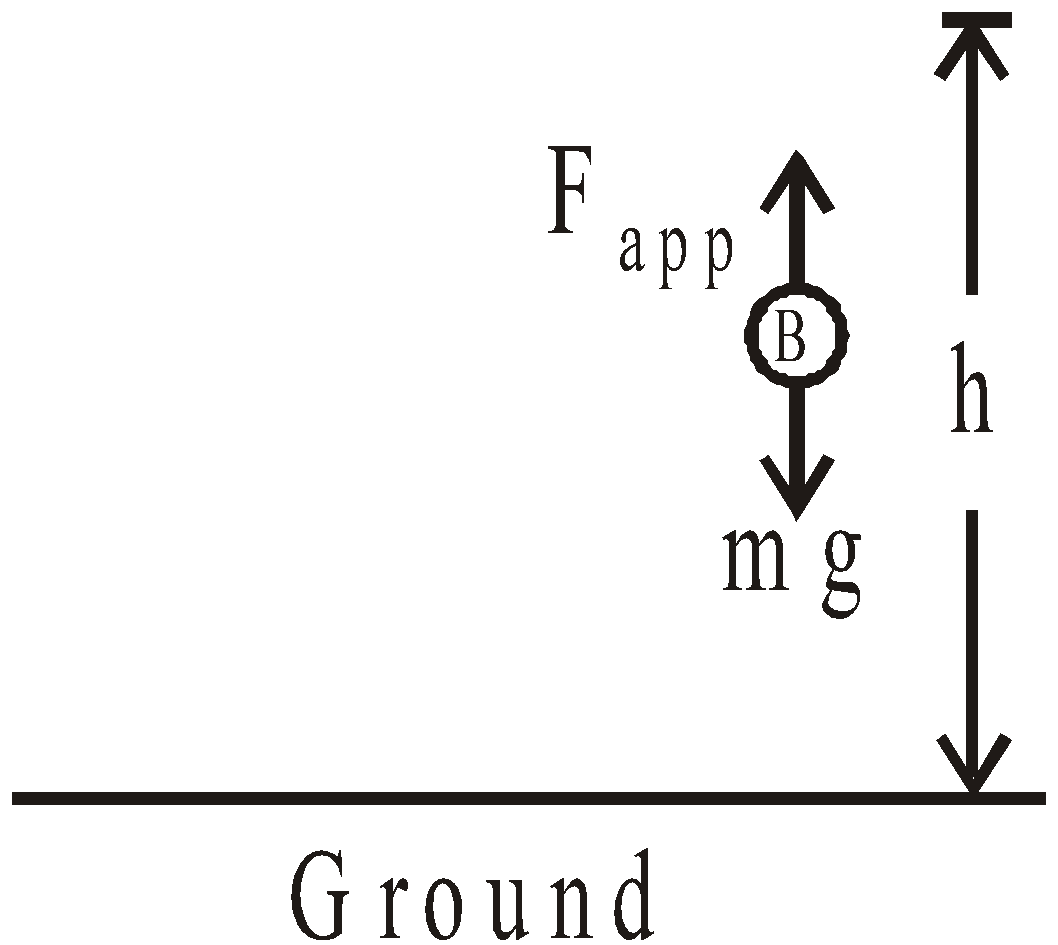
Raised with constant speed – no net work done.
Potential energy (Ep): energy stored in a position.
Gravitational potential energy: energy related to height – Ep = mg ∆h
Independent of path followed - only ∆h matters ∆h.
Elastic potential energy: energy stored in a spring – Ep = 1/2kx2
In a Force-extension graph, the area is the work done, and the gradient is k.
Other energies: Electric, Magnetic, Chemical, Nuclear, Thermal, Vibration, Light…
Dissipation: Energy transformed into thermal energy (internal energy of a body), sound.
Power (P)
“Power is the rate of energy transfer.” P = ∆W/∆t = ∆pv/∆t = Fv
Measured in W (watts).
Efficiency
Energy transferred = useful energy + wasted enery (never say lost energy!)
Efficiency = useful energy out/total energy in = useful power out/total power.
Efficiency is always smaller than 100% – frictional forces.
WORK, POWER AND ENERGY
WORK
WORK DONE BY A CONSTANT FORCE
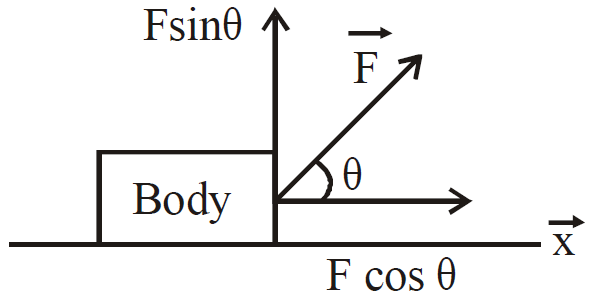
- When θ = 0° then W = Fx
- When θ is between 0 and π/2 then
- When θ = π/2 then W = Fx cos 90° = 0 (zero)
- ∴ When θ is between π/2 and π then
WORK DONE BY A VARIABLE FORCE
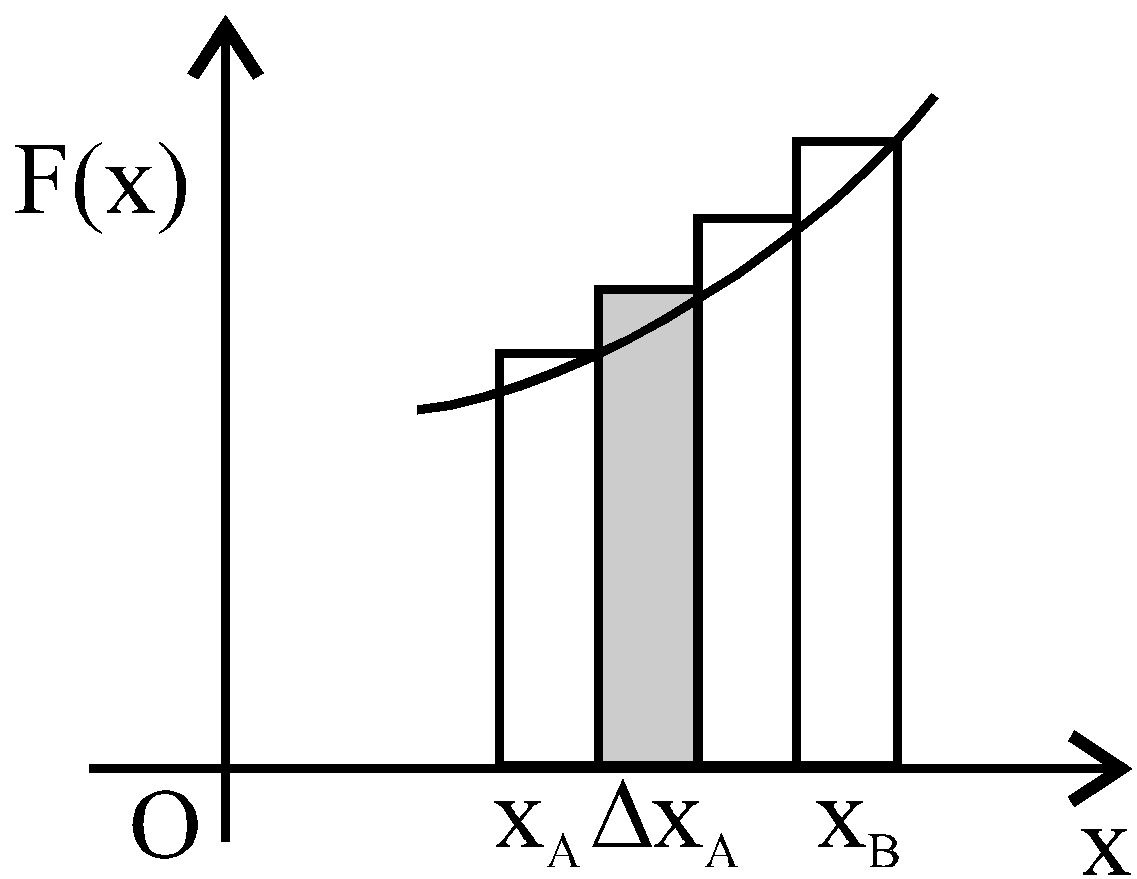

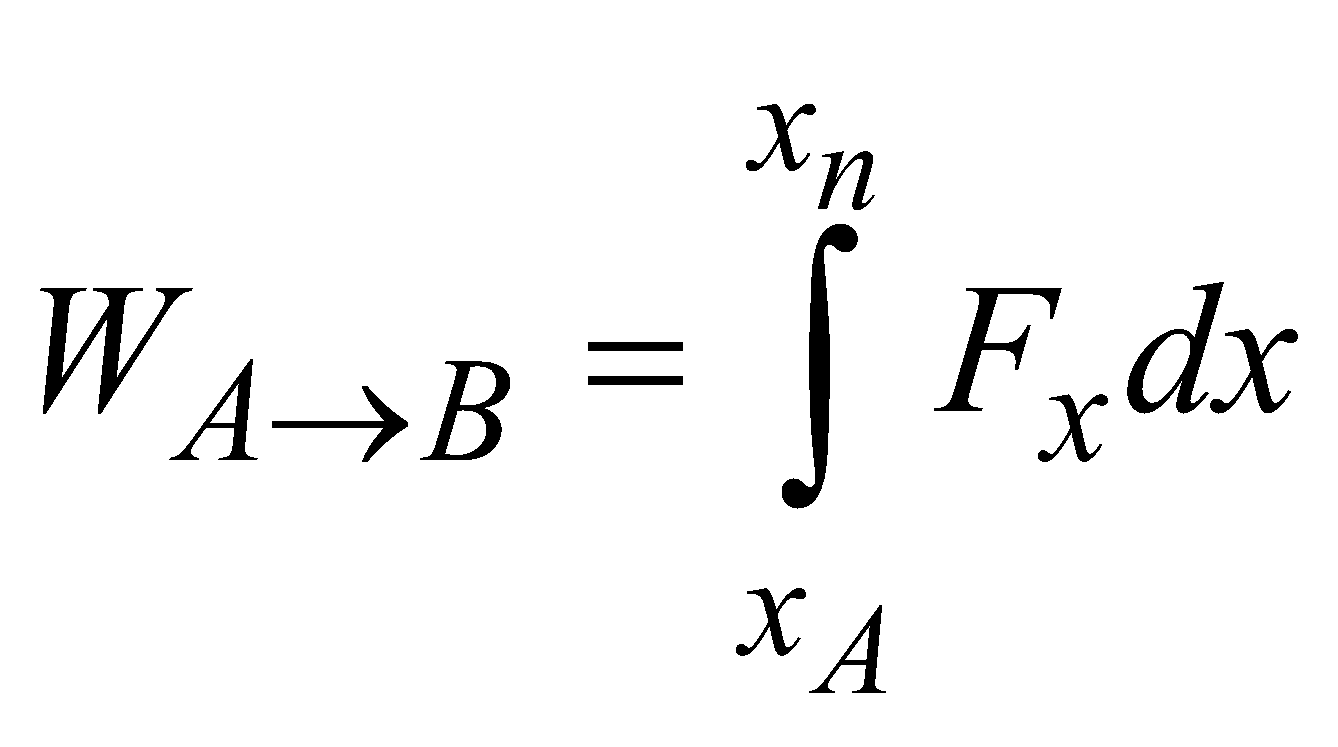
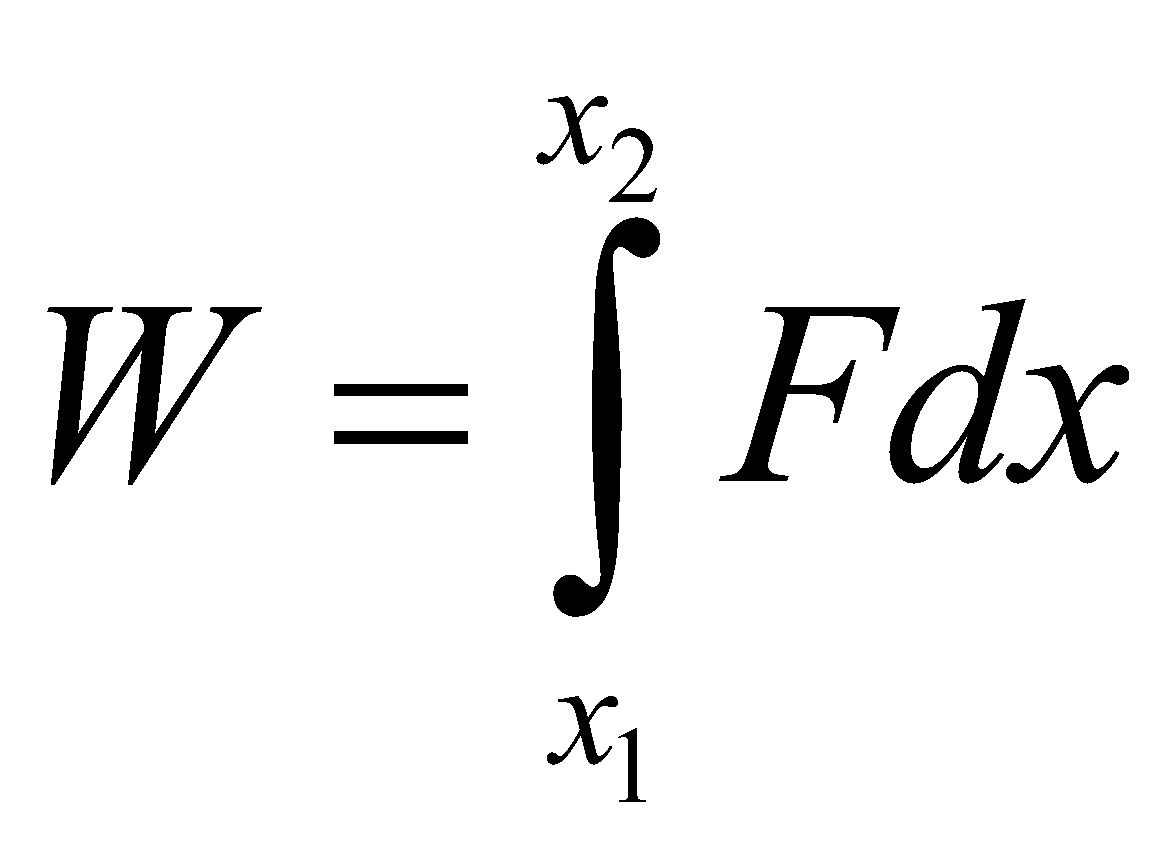 = area under force displacement graph
= area under force displacement graph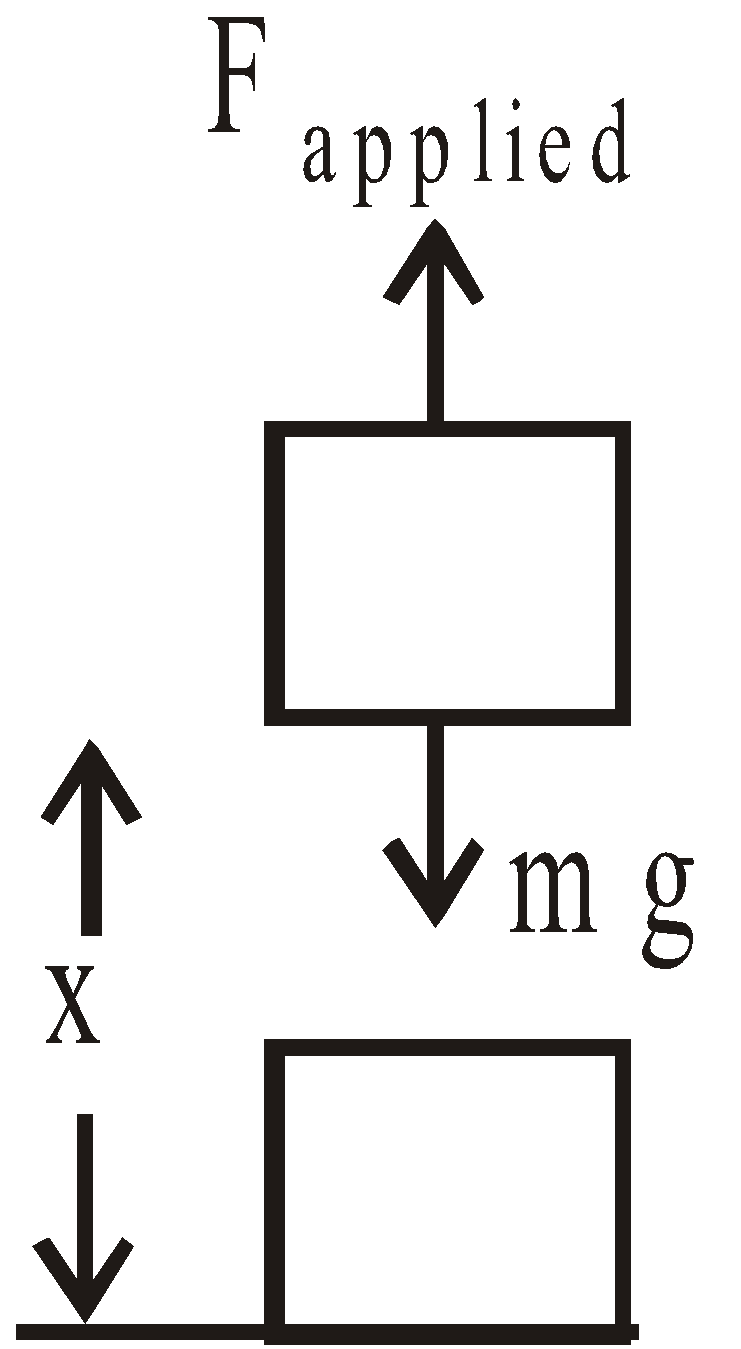
ENERGY
POTENTIAL ENERGY
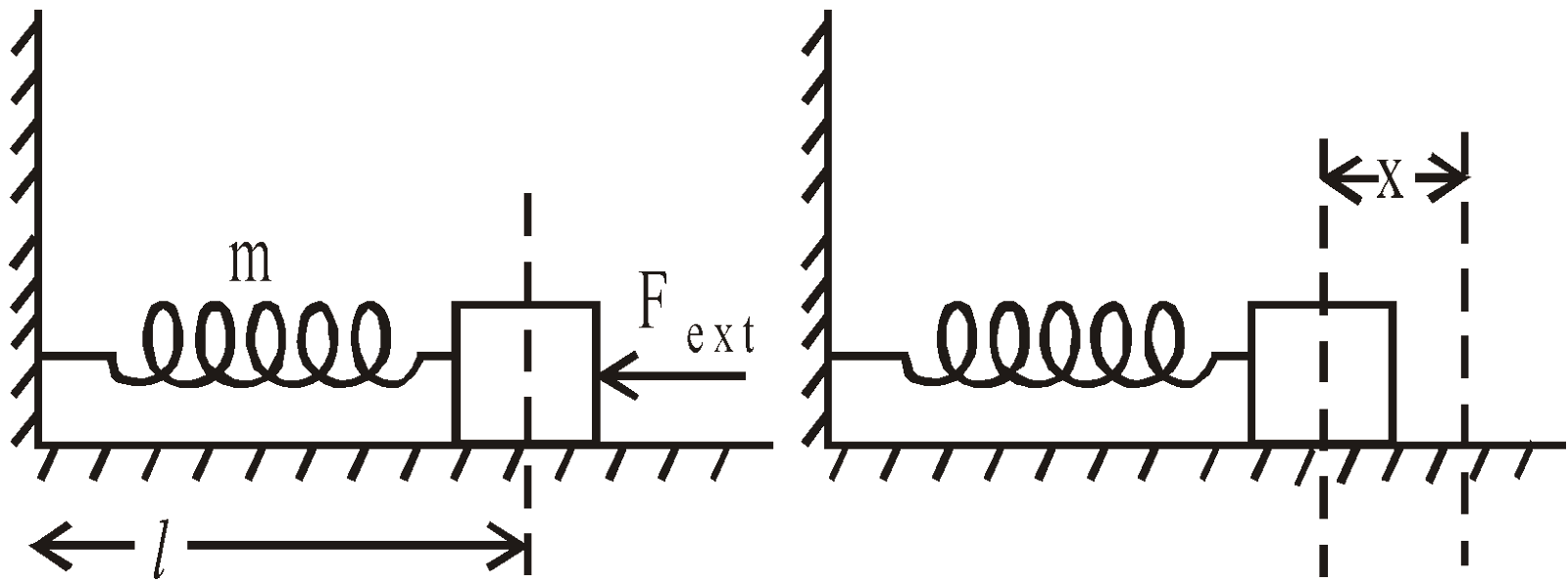
KINETIC ENERGY
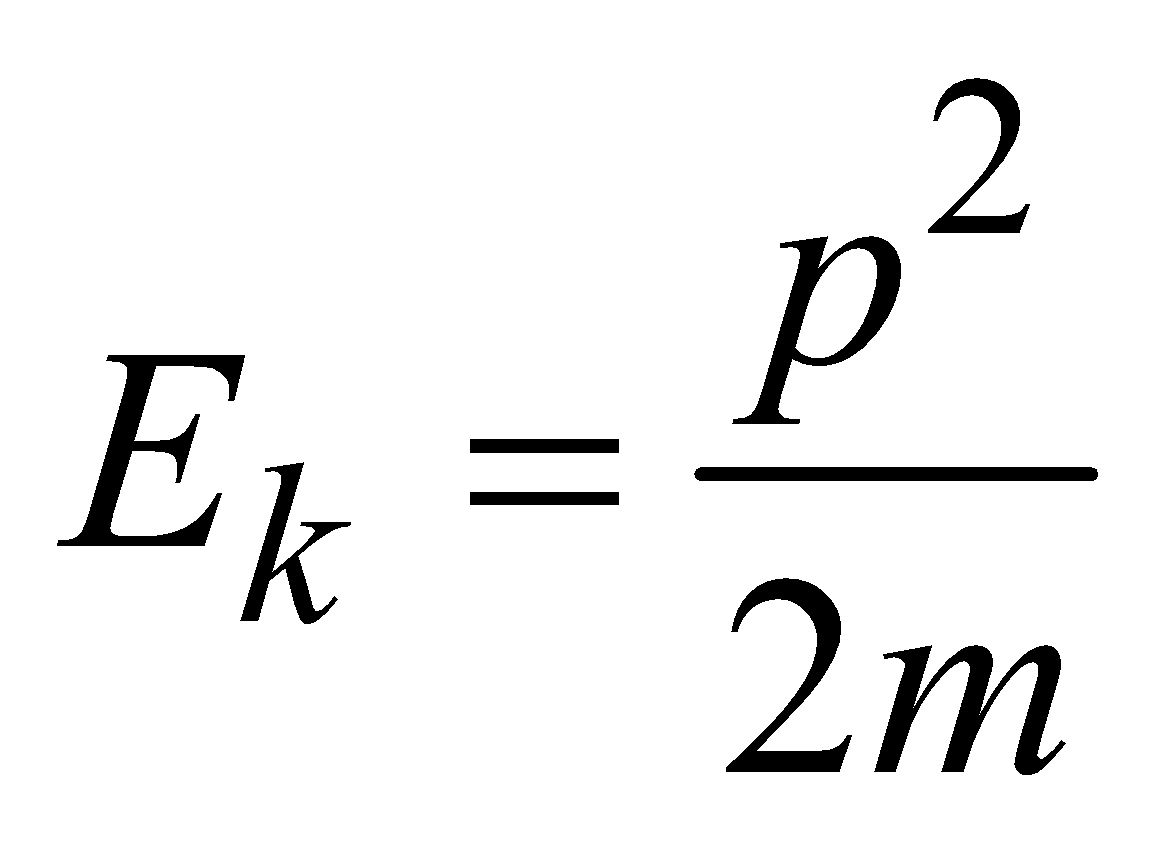 …(iii)
…(iii)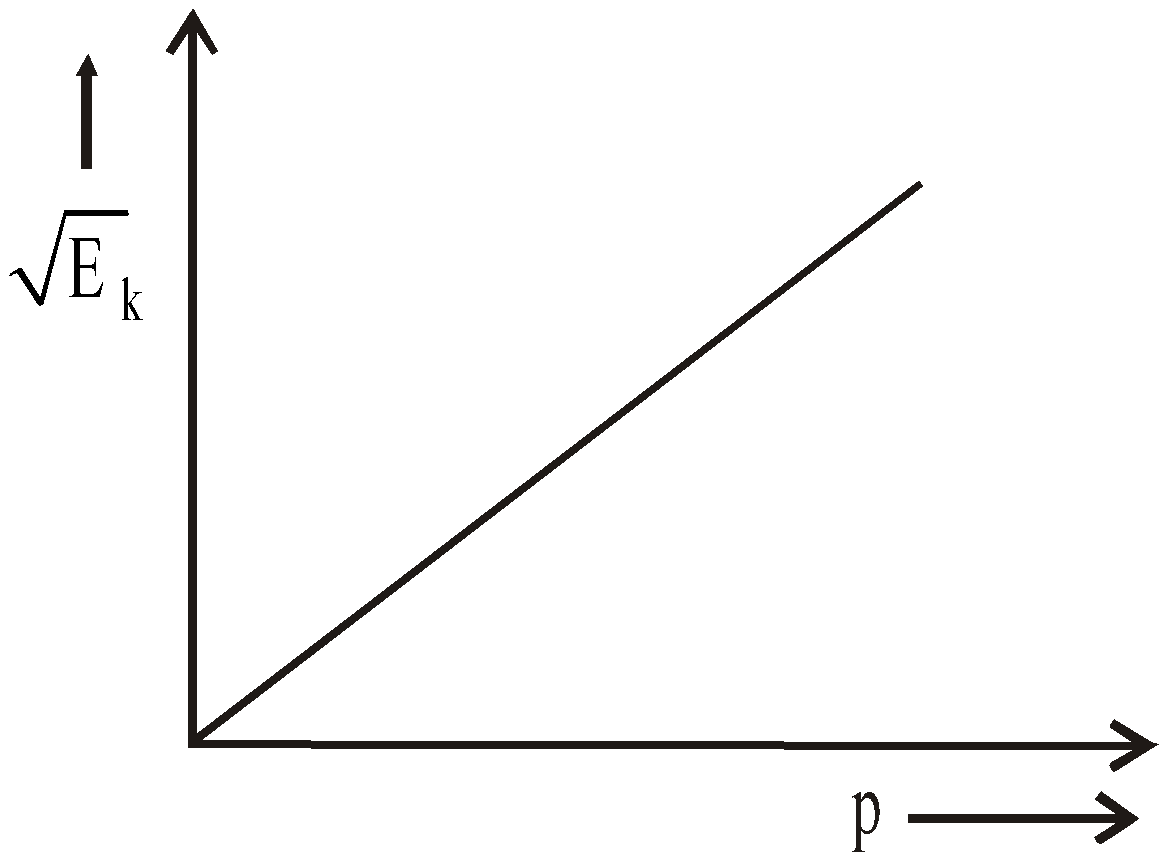
- Work done by the conservative force in moving a body in a closed loop is zero.
- If the momenta of two bodies are equal then the kinetic energy of lighter body will be more.
- If the kinetic energies of two bodies are same then the momentum of heavier body will be more.
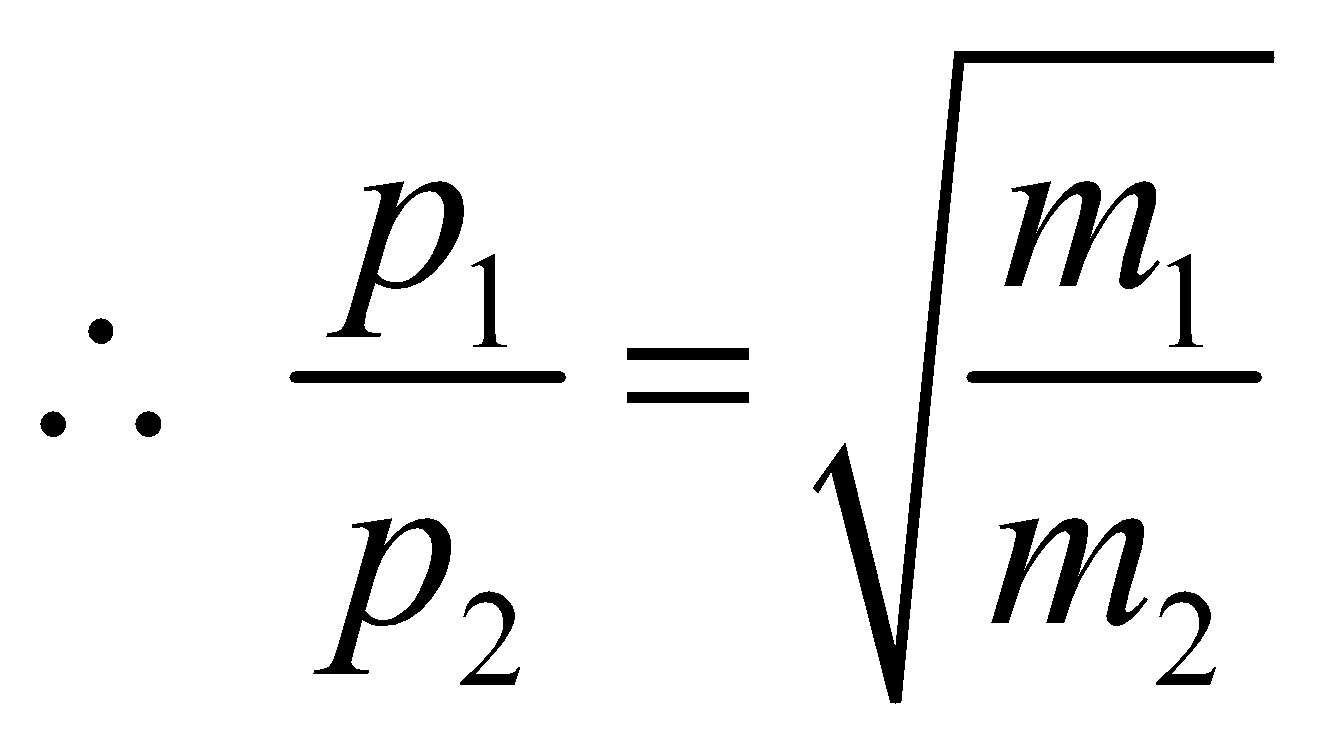
WORK-ENERGY THEOREM
LAW OF CONSERVATION OF MECHANICAL ENERGY
LAW OF CONSERVATION OF ENERGY
- Work done against friction on horizontal surface = μ mgx and work done against force of friction on inclined plane = (μmg cosθ) x where μ = coefficient of friction.
- If a body moving with velocity v comes to rest after covering a distance ‘x’ on a rough surface having coefficient of friction μ, then (from work energy theorem), 2μ gx = v2. Here retardation is
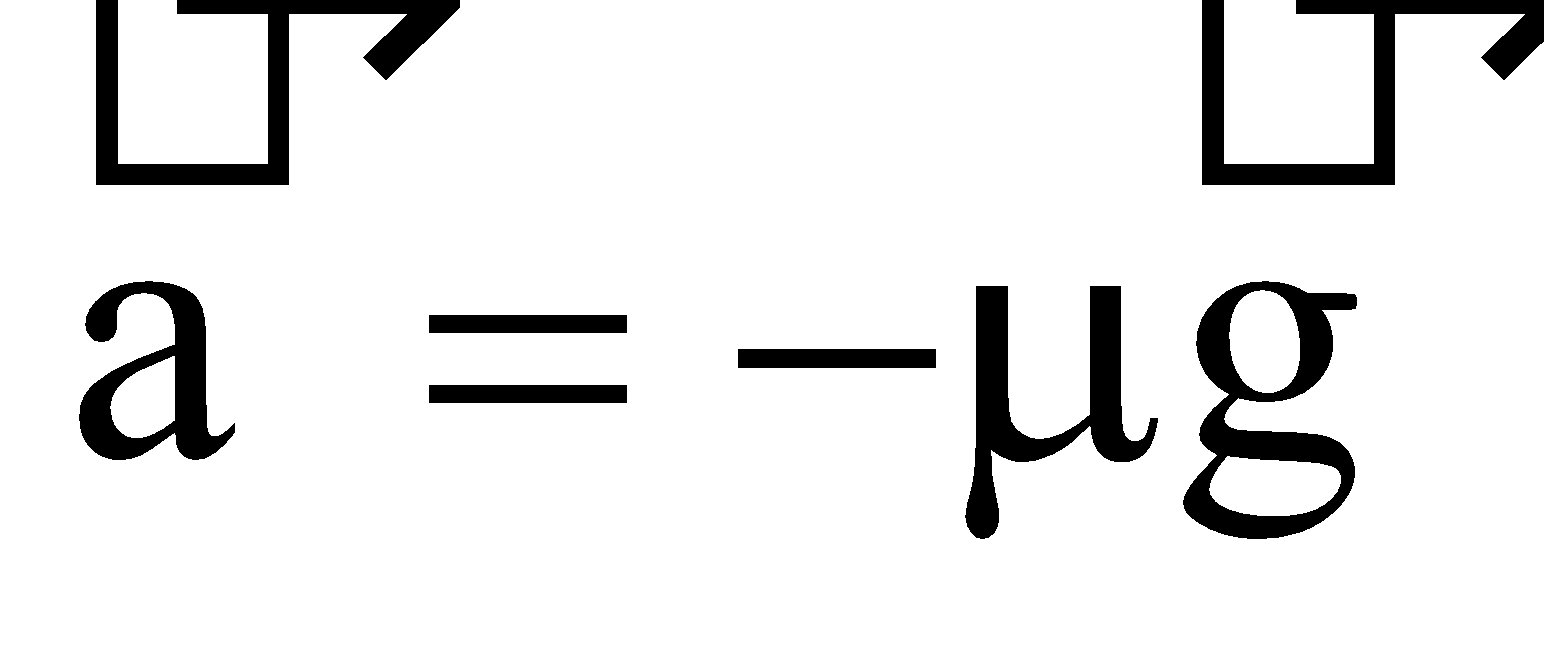
- Work done by a centripetal force is always zero.
- Potential energy of a system decreases when a conservative force does work on it.
- If the speed of a vehicle is increased by n times, then its stopping distance becomes n2 times and if momentum is increased by n times then its kinetic energy increases by n2 times.
- Stopping distance of the vehicle
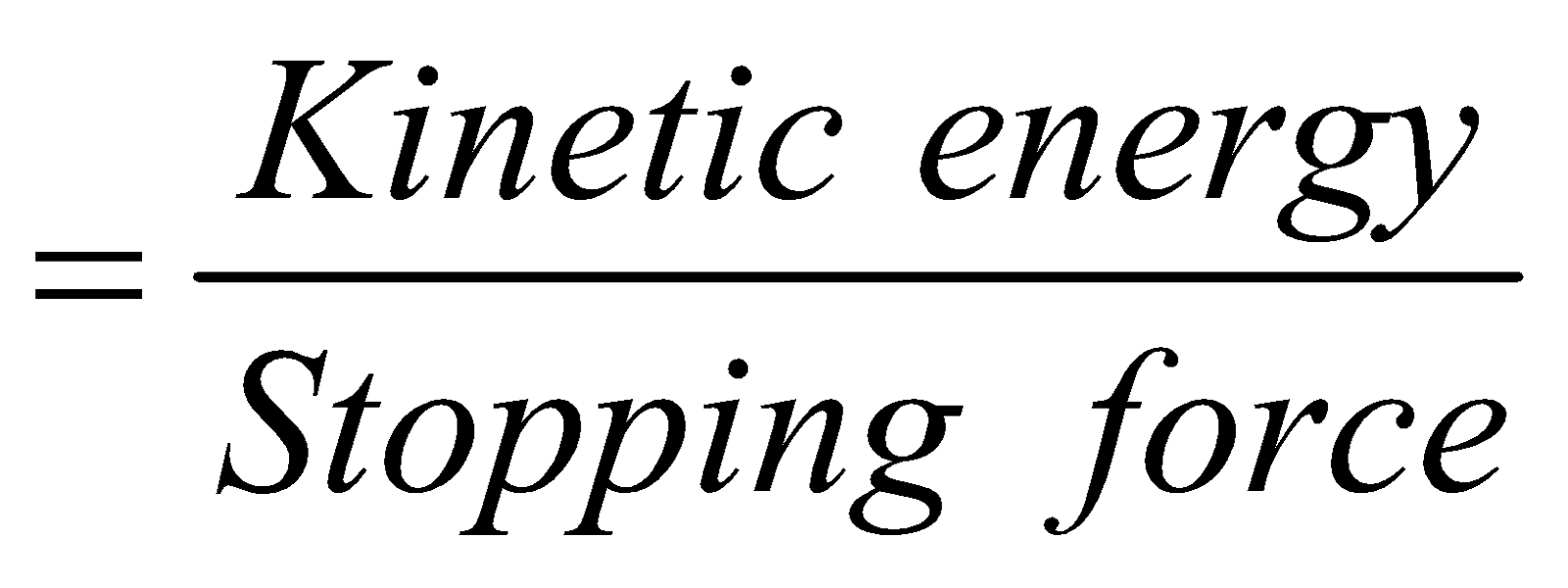
- Two vehicles of masses M1 and M2 are moving with velocities u1 and u2 respectively. When they are stopped by the same force, their stopping distance are in the ratio as follows :
Since the retarding force F is same in stopping both the vehicles. Let x1 and x2 are the stopping distances of vehicles of masses M1 & M2 respectively, then
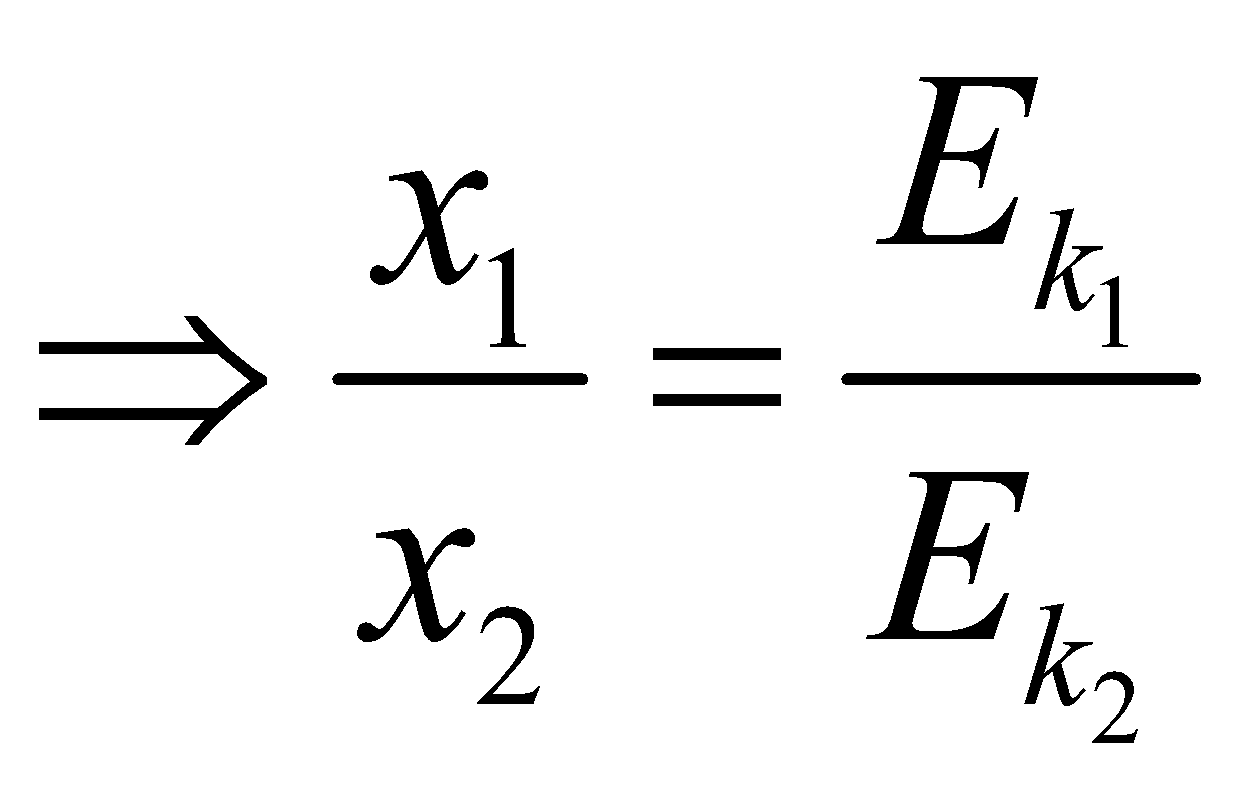 ….(ii)
….(ii)M1 & M2 respectively, then from first equation of motion (v = u+at)
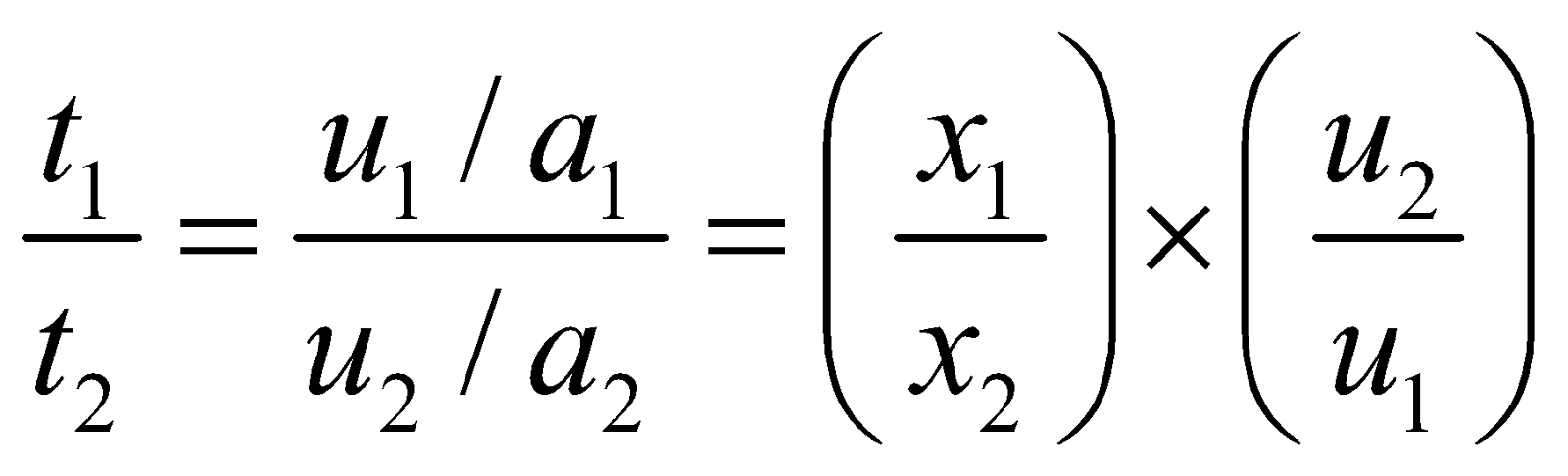
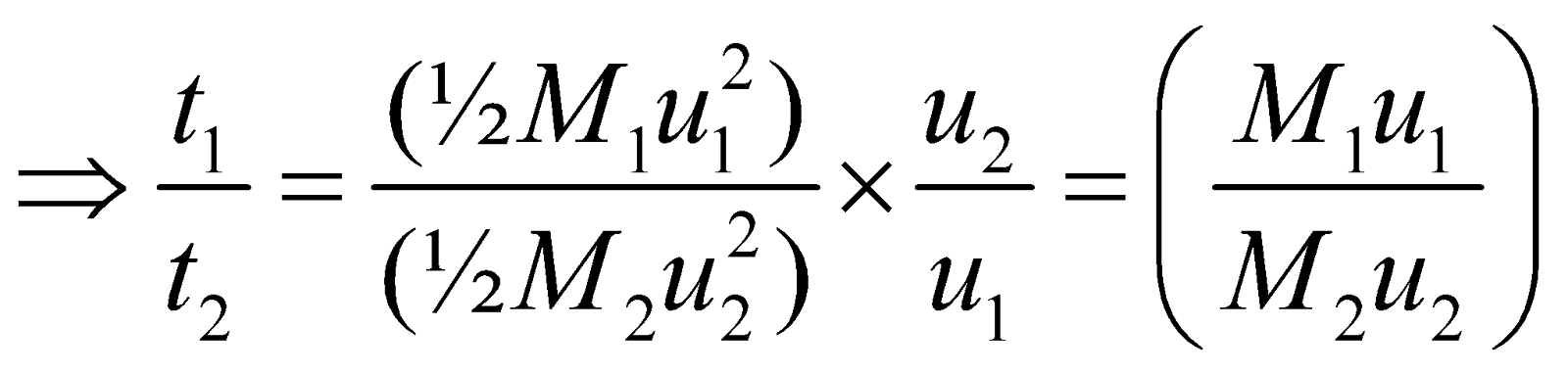
- If
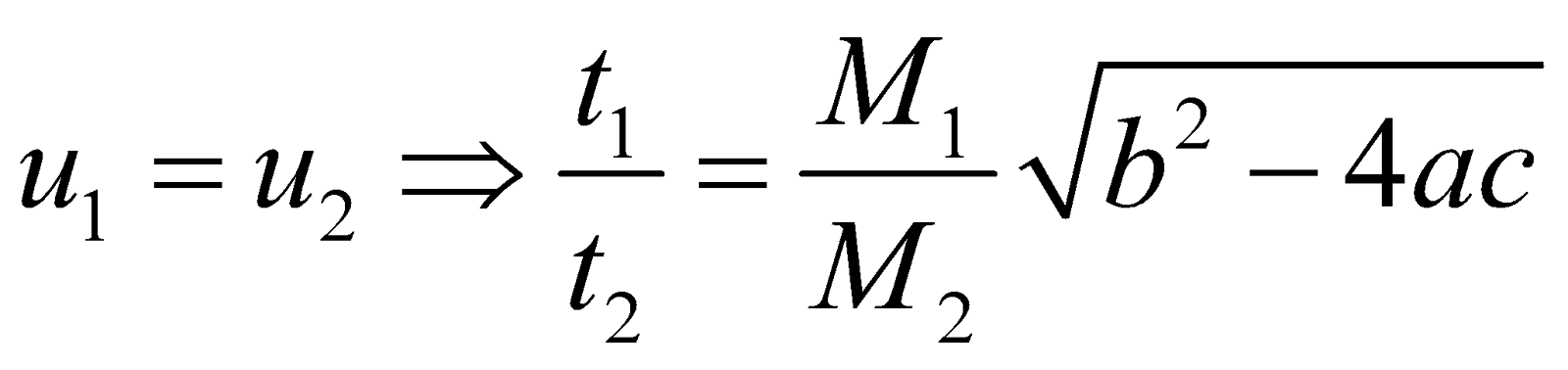
- If
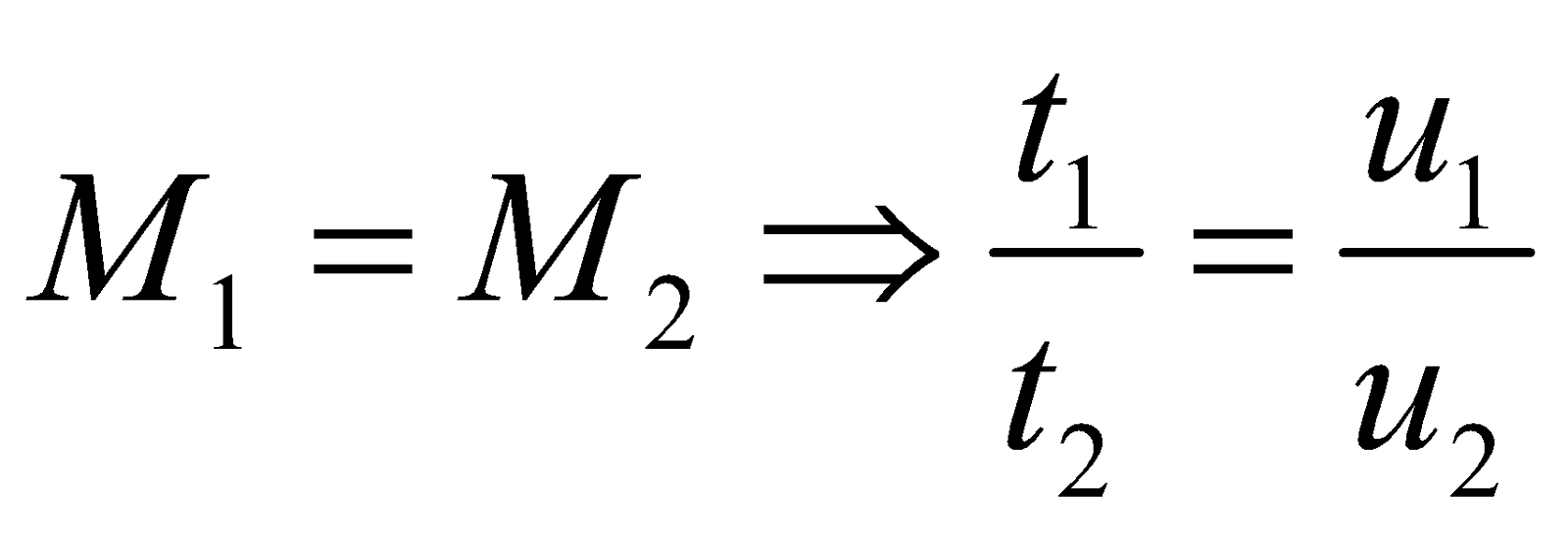
- If M1u1 = M2u1 ⇒ t1 = t2 and
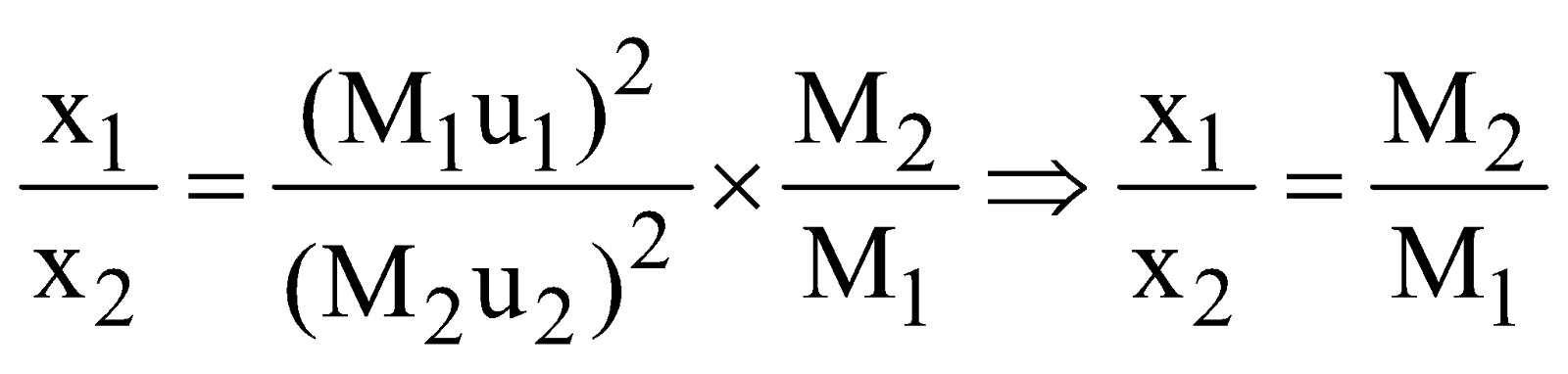
- Consider two vehicles of masses M1 & M2 respectively.
- If kinetic energy of a body is doubled, then its momentum becomes
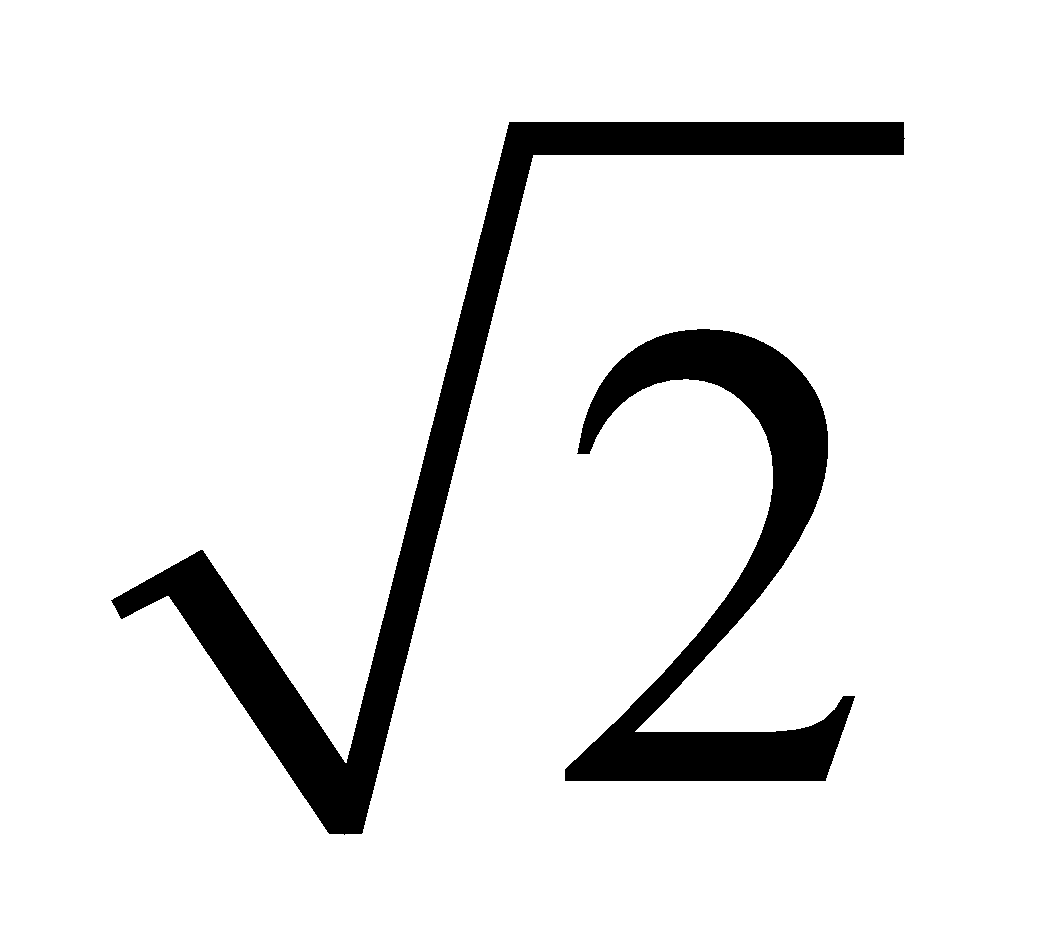 times,
times, 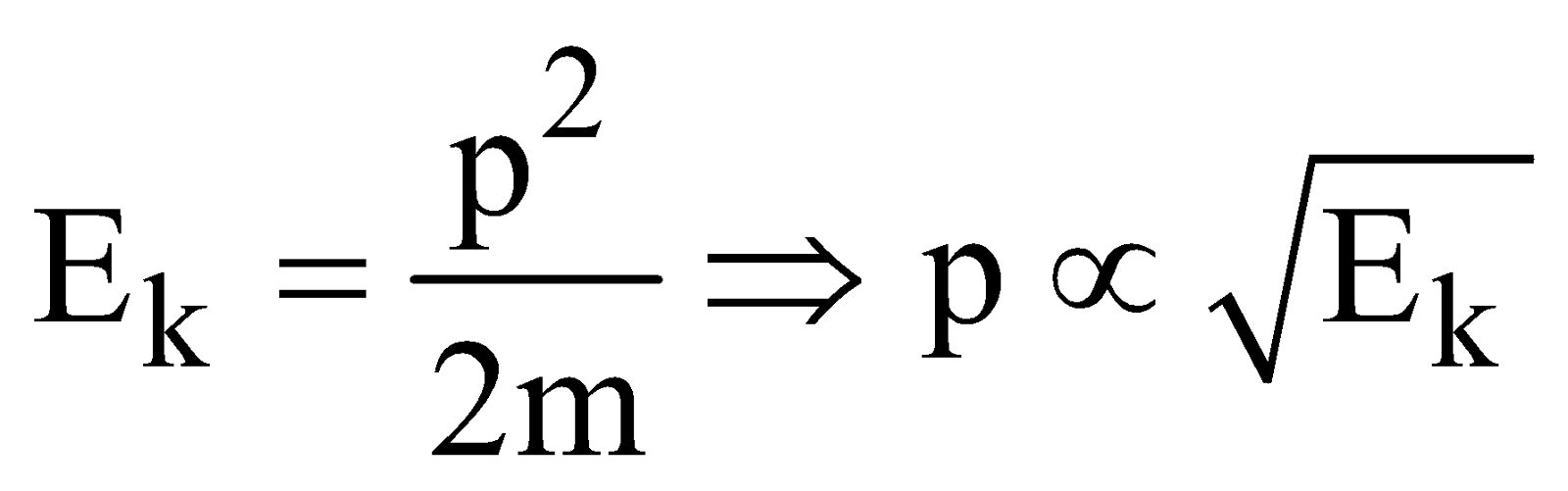
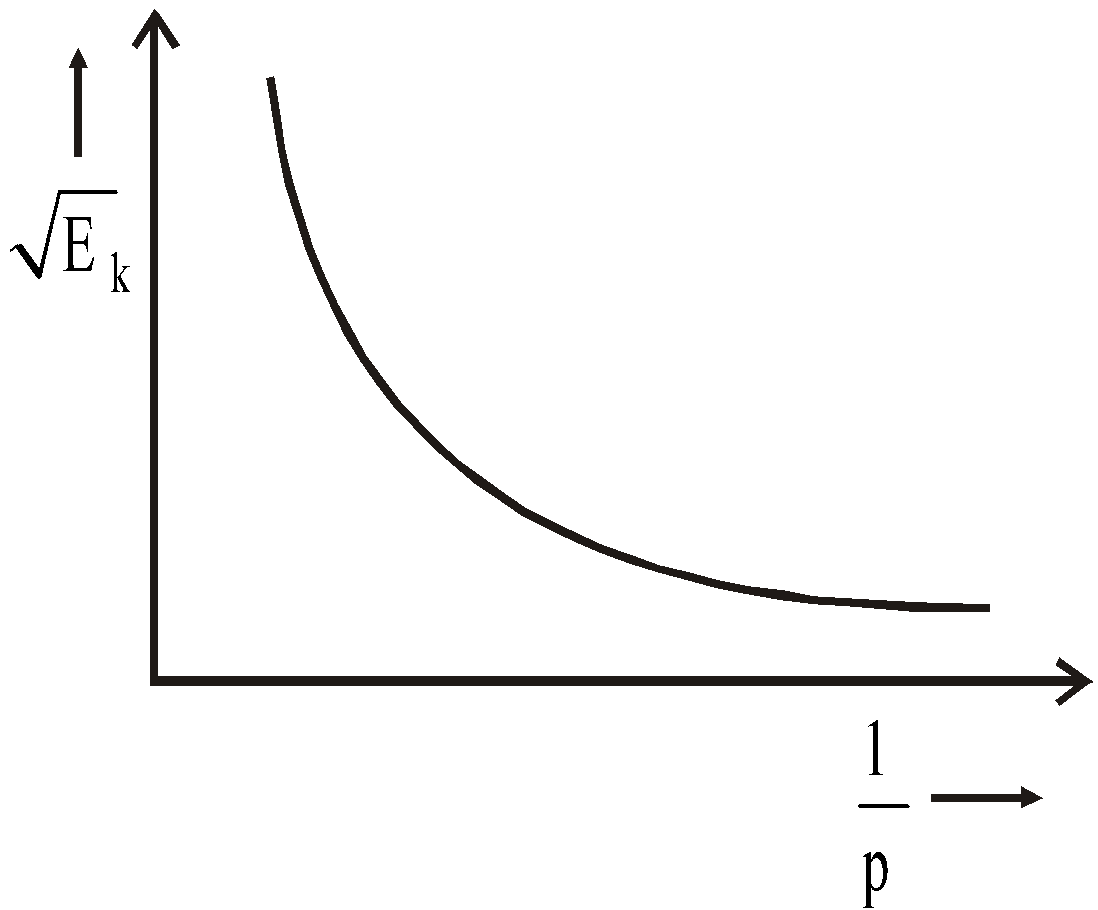
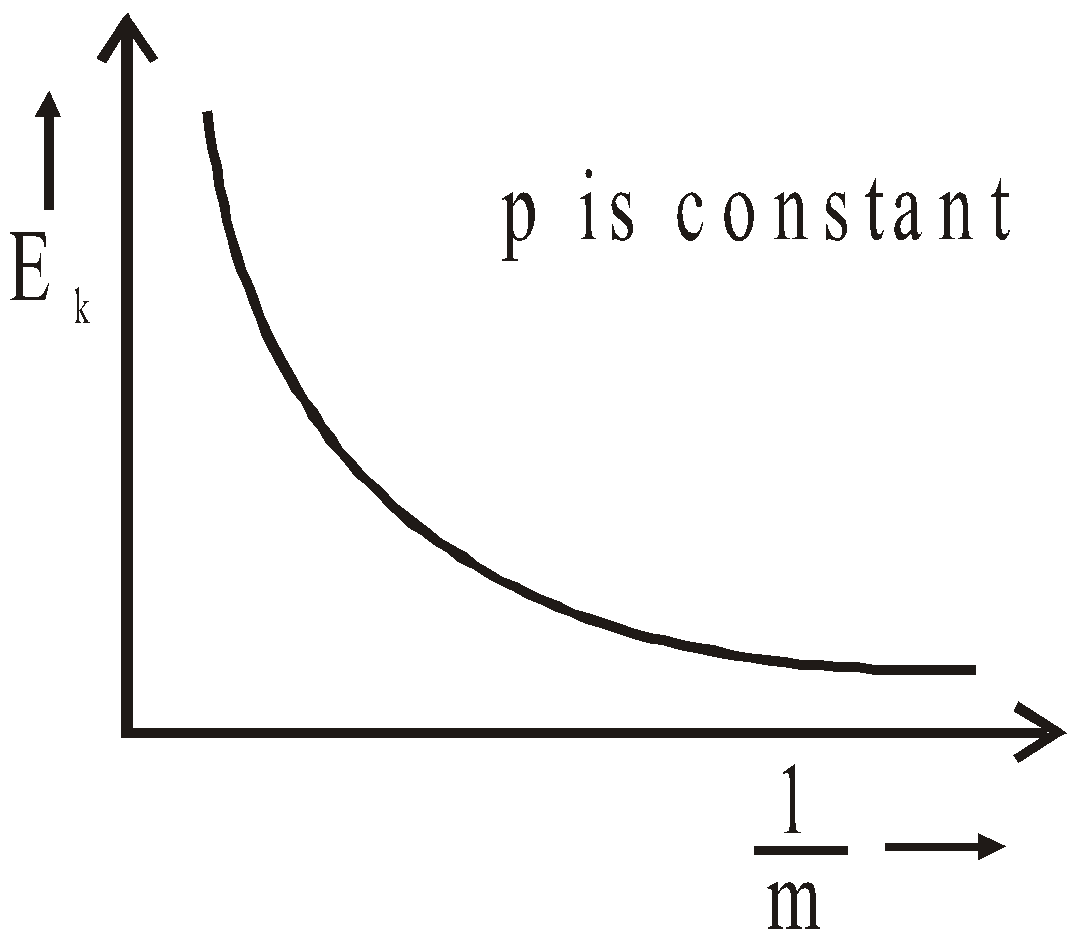
- If two bodies of masses m1 and m2 have equal kinetic energies, then their velocities are inversely proportional to the square root of the respective masses. i.e.
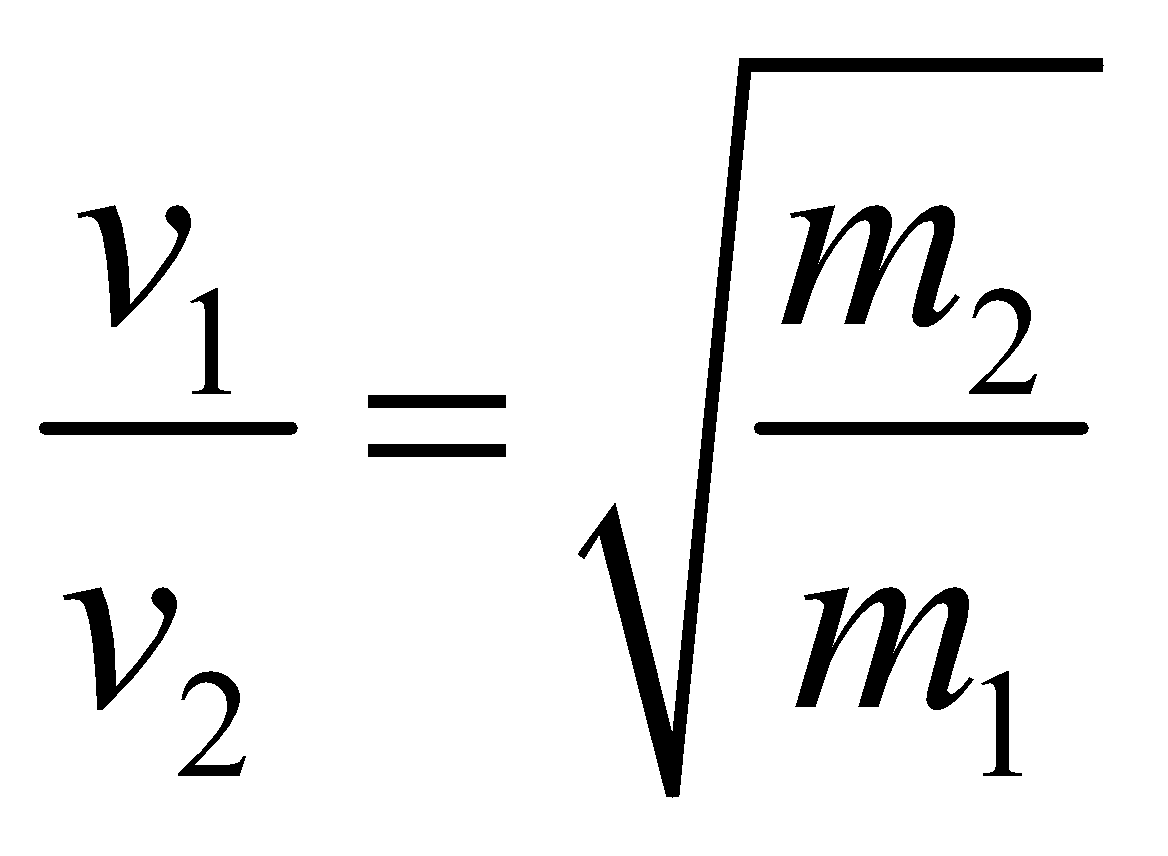
- The spring constant of a spring is inversely proportional to the no. of turns i.e.
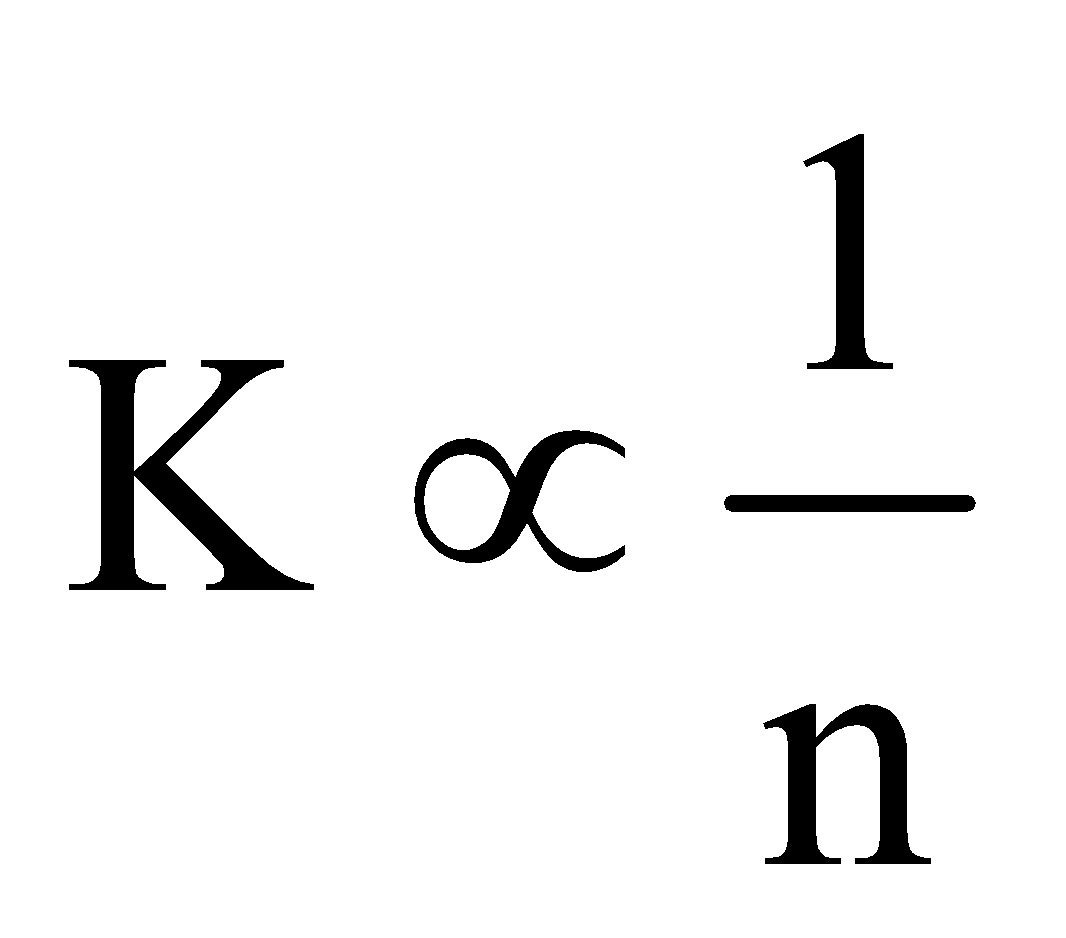 or kn = const.
or kn = const.
- Spring constant : The spring constant of a spring is inversely proportional to length i.e.,
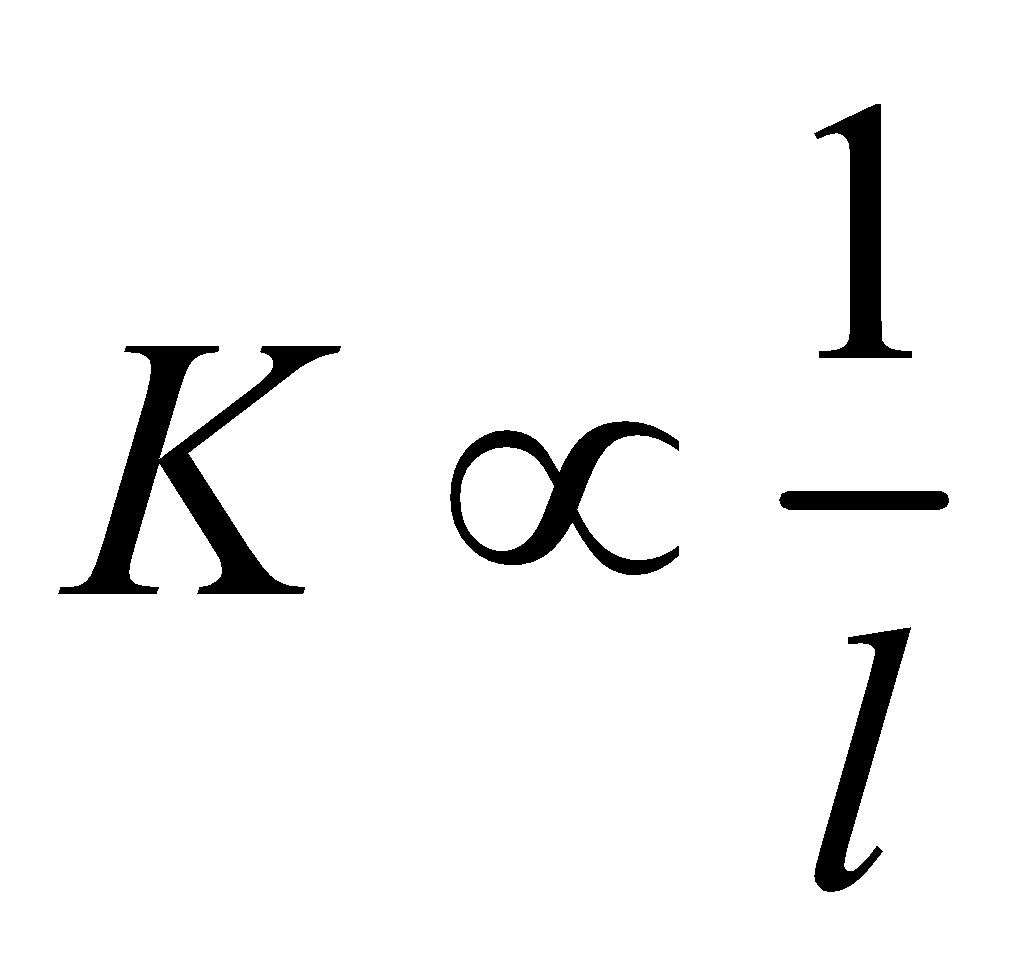 or Kl = constant.
or Kl = constant.- If a spring is divided into n equal parts, the spring constant of each part = nK.
- If spring of spring constant K1, K2, K3 ………. are connected in series, then effective force constant
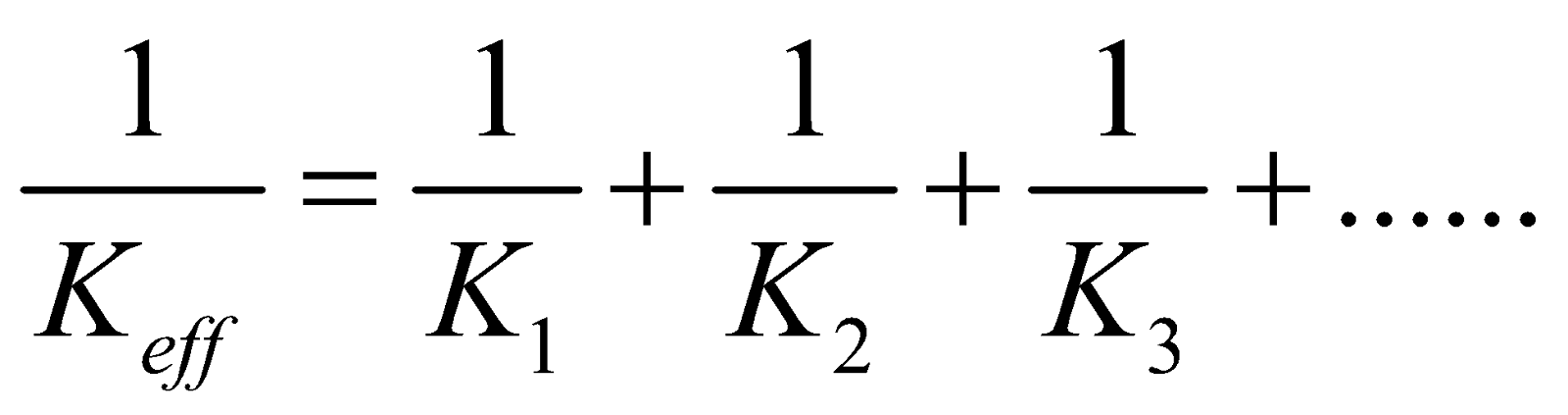
- If spring of spring constant K1, K2, K3……….. are connected in parallel, then effective spring constant
Keff = K1 + K2 + K3 +………….
POWER
COLLISION

- Elastic collision : The collision in which both the momentum and kinetic energy of the system remains conserved is called elastic collision.
- Inelastic collision : The collision in which only the momentum of the system is conserved but kinetic energy is not conserved is called inelastic collision.
COEFFICIENT OF RESTITUTION (OR COEFFICIENT OF RESILIENCE)
- 0 < e < 1 (Inelastic collision)
- For perfectly elastic collision, e = 1
- For a perfectly inelastic collision, e = 0
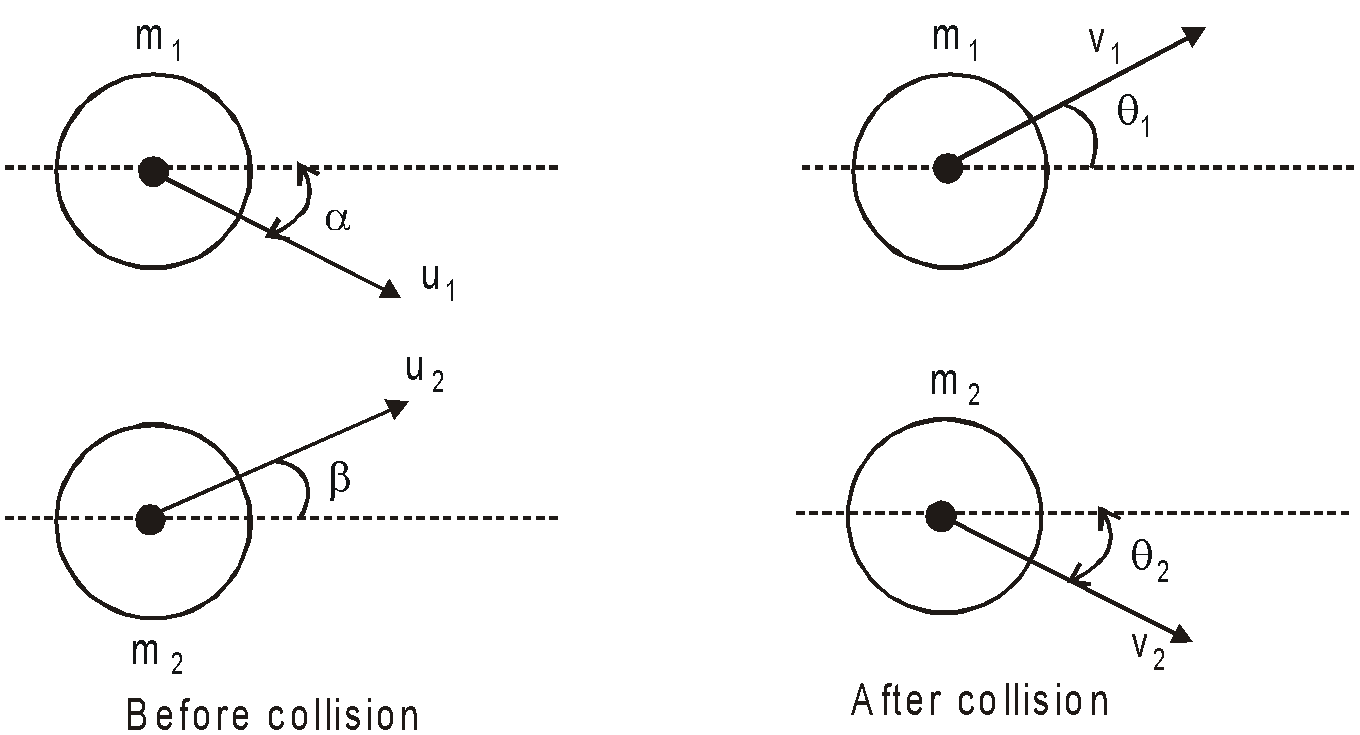
OBLIQUE ELASTIC COLLISION
ELASTIC COLLISION IN ONE DIMENSION (HEAD ON)

- If M1 = M2 and u2 = 0 then v1 = 0 and v2 = u1. Under this condition the first particle comes to rest and the second particle moves with the velocity of first particle after collision. In this state there occurs maximum transfer of energy.
- If M1>> M2 and (u2=0) then, v1 = u1, v2 = 2u1 under this condition the velocity of first particle remains unchanged and velocity of second particle becomes double that of first.
- If M1 << M2 and (u2 = 0) then v1 = –u1 and v2 =
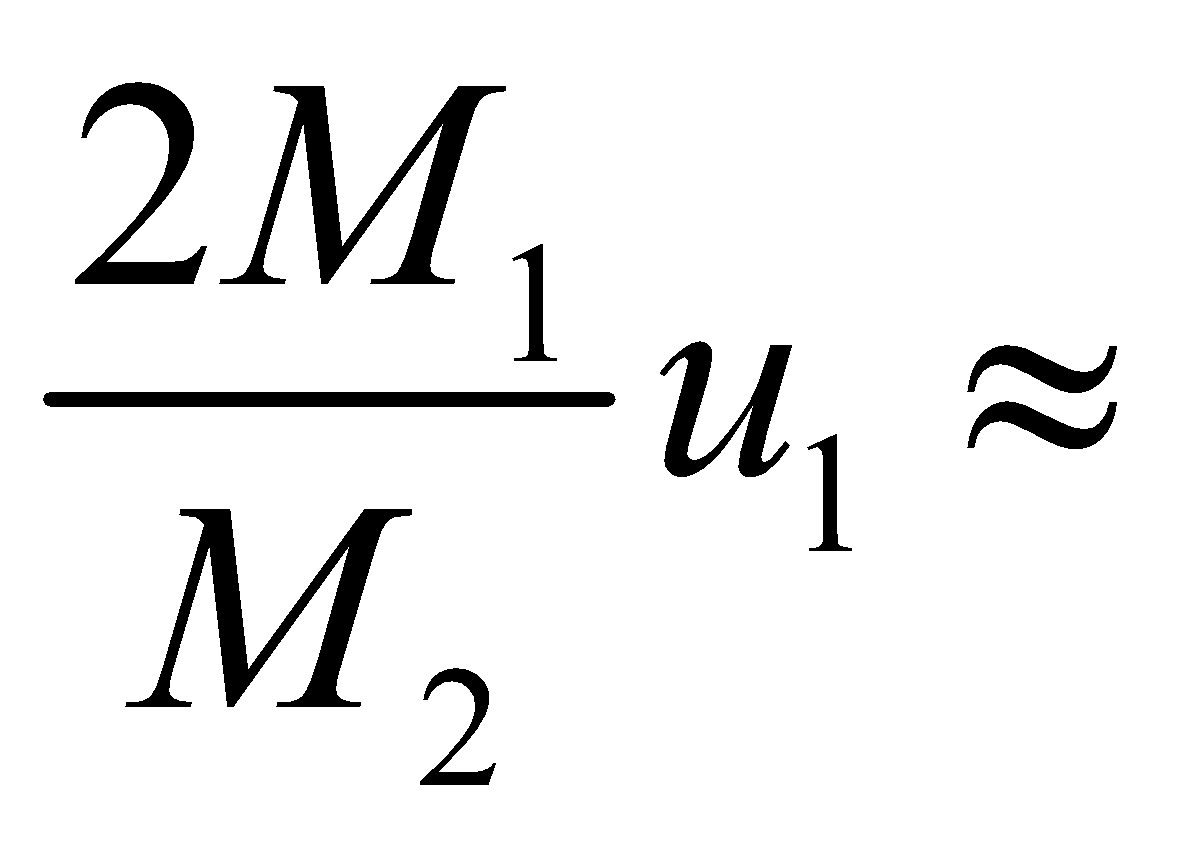 0 under this condition the second particle remains at rest while the first particle moves with the same velocity in the opposite direction.
0 under this condition the second particle remains at rest while the first particle moves with the same velocity in the opposite direction. - If M1 = M2 = M but u2 ≠0 then v1 = u2 i.e., the particles mutually exchange their velocities.
- If second body is at rest i.e., u2 = 0, then fractional decrease in kinetic energy of mass M1, is given by
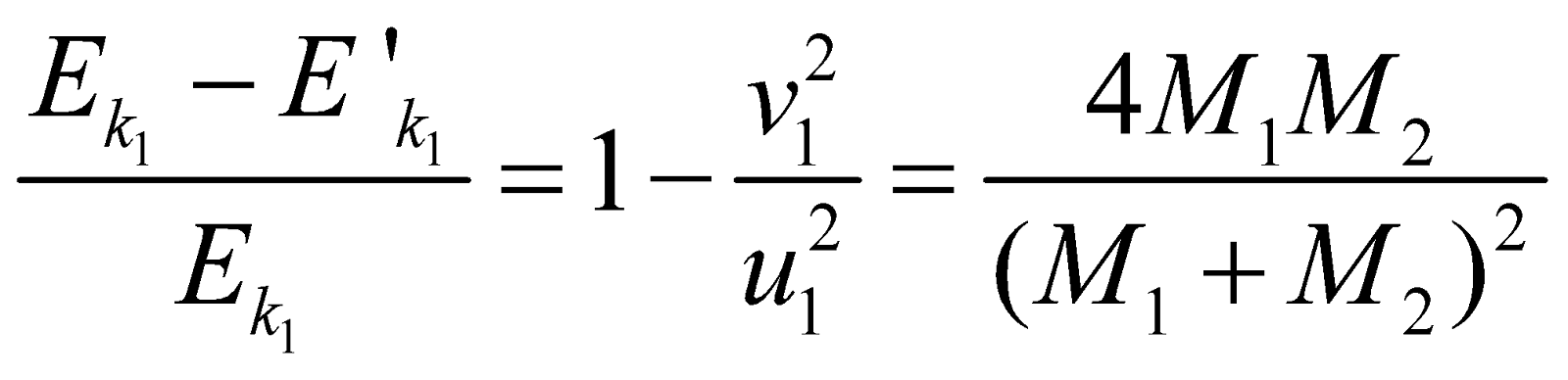
INELASTIC COLLISION
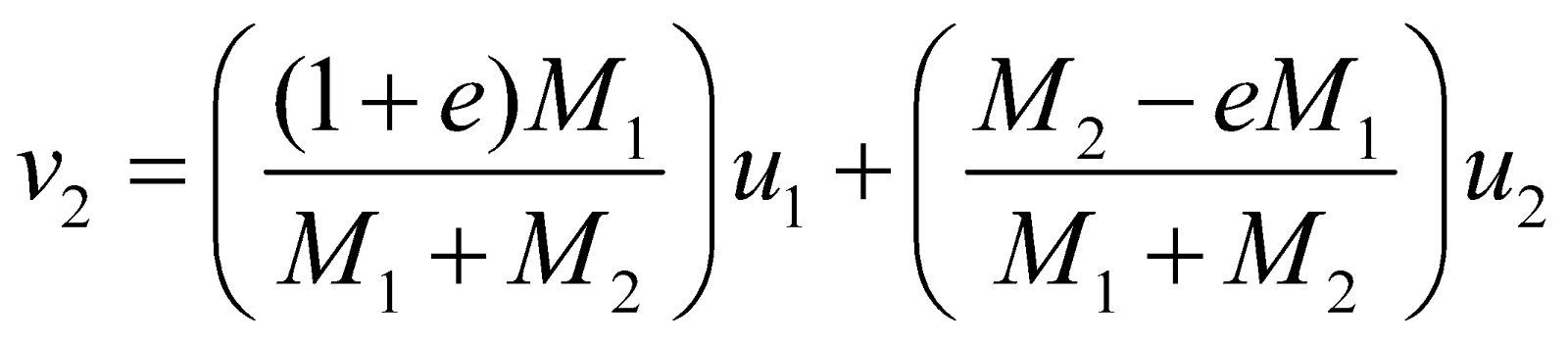 …(iv)
…(iv)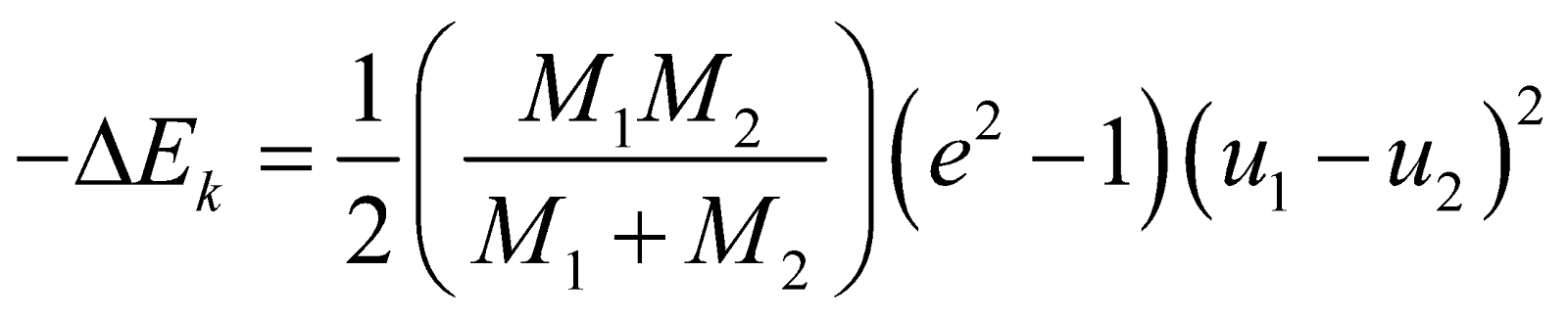 …(v)
…(v)PERFECTLY INELASTIC COLLISION
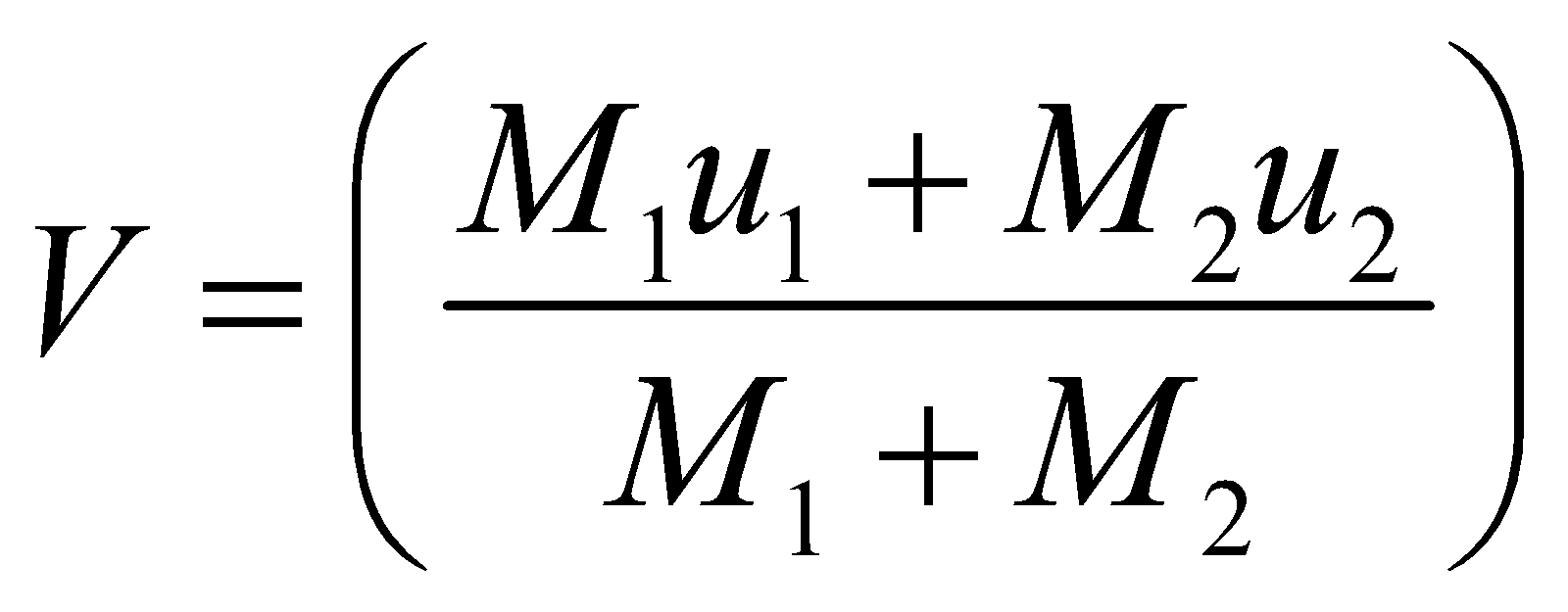 …(ii)
…(ii)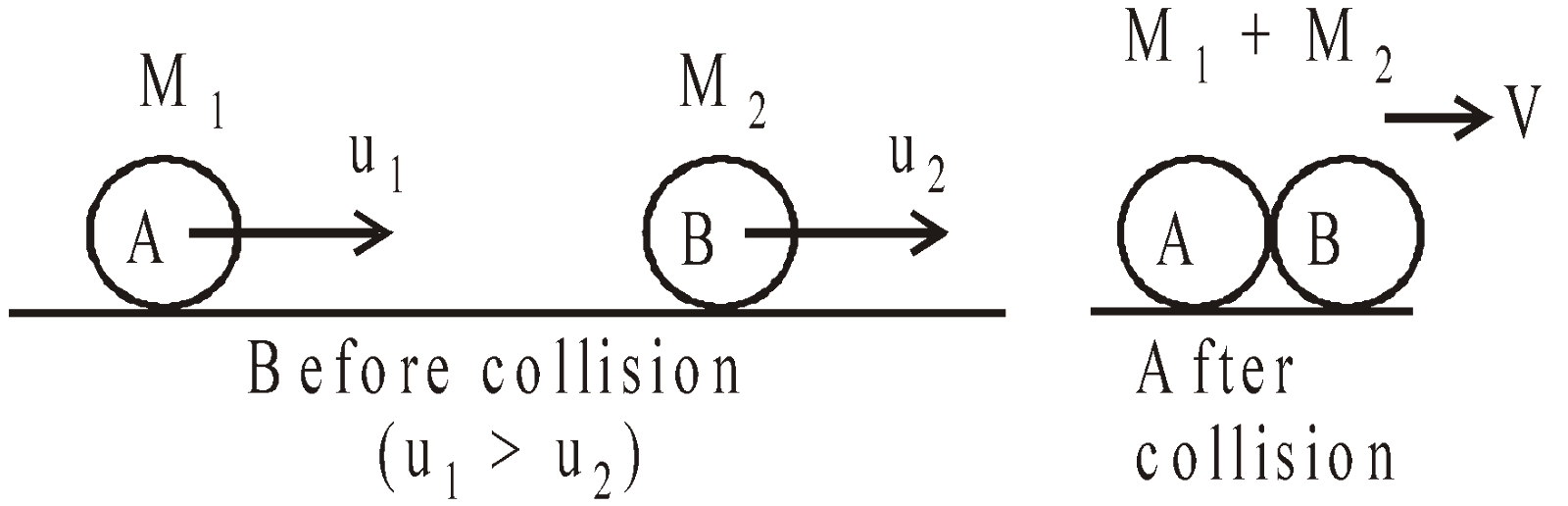
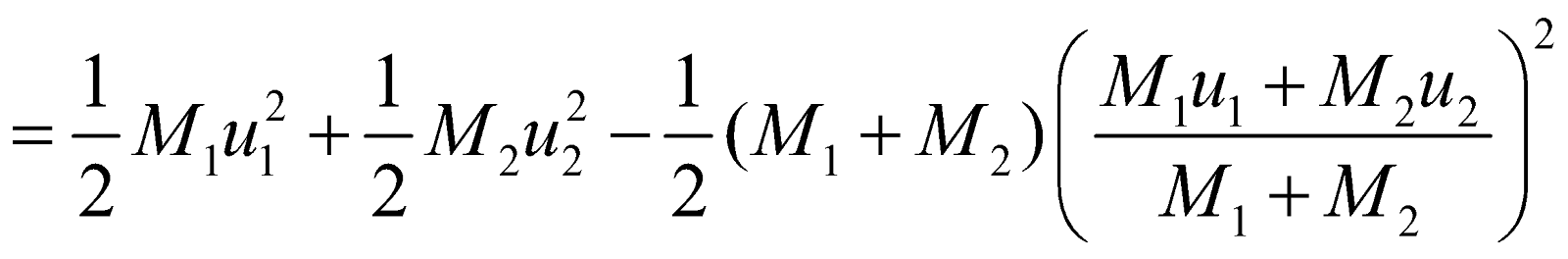
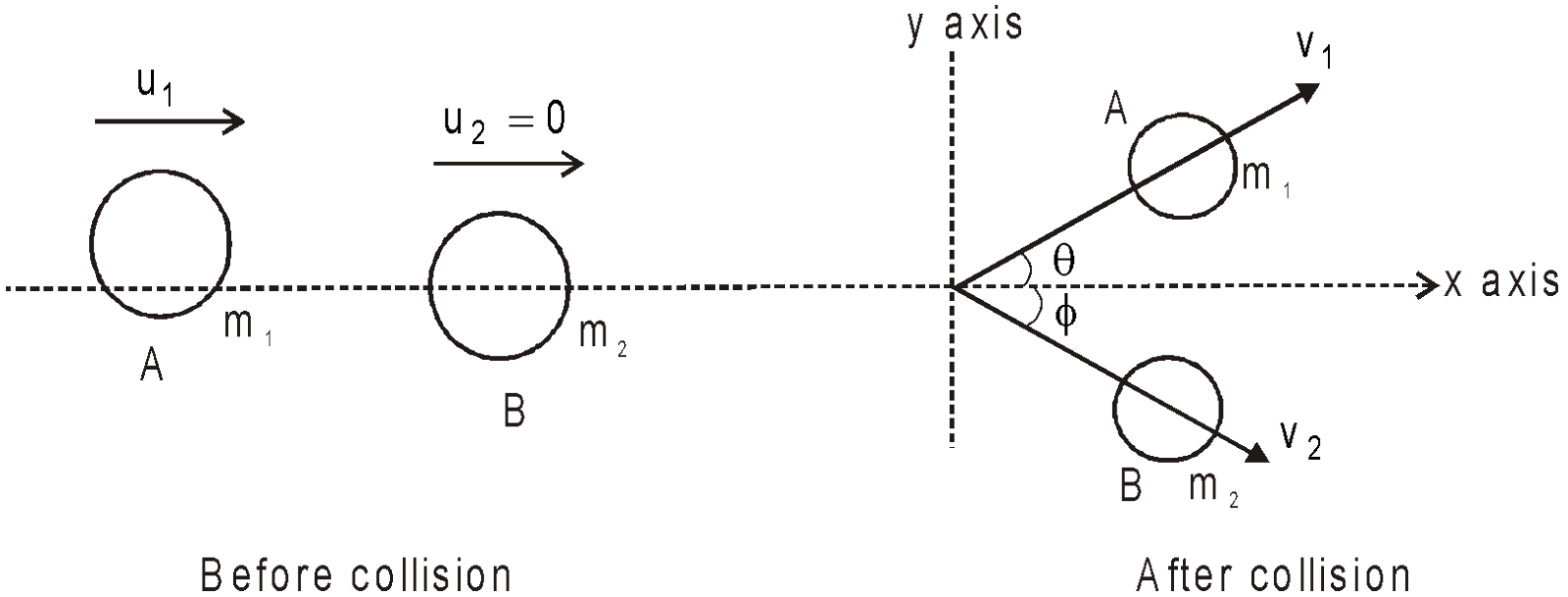
OBLIQUE COLLISION
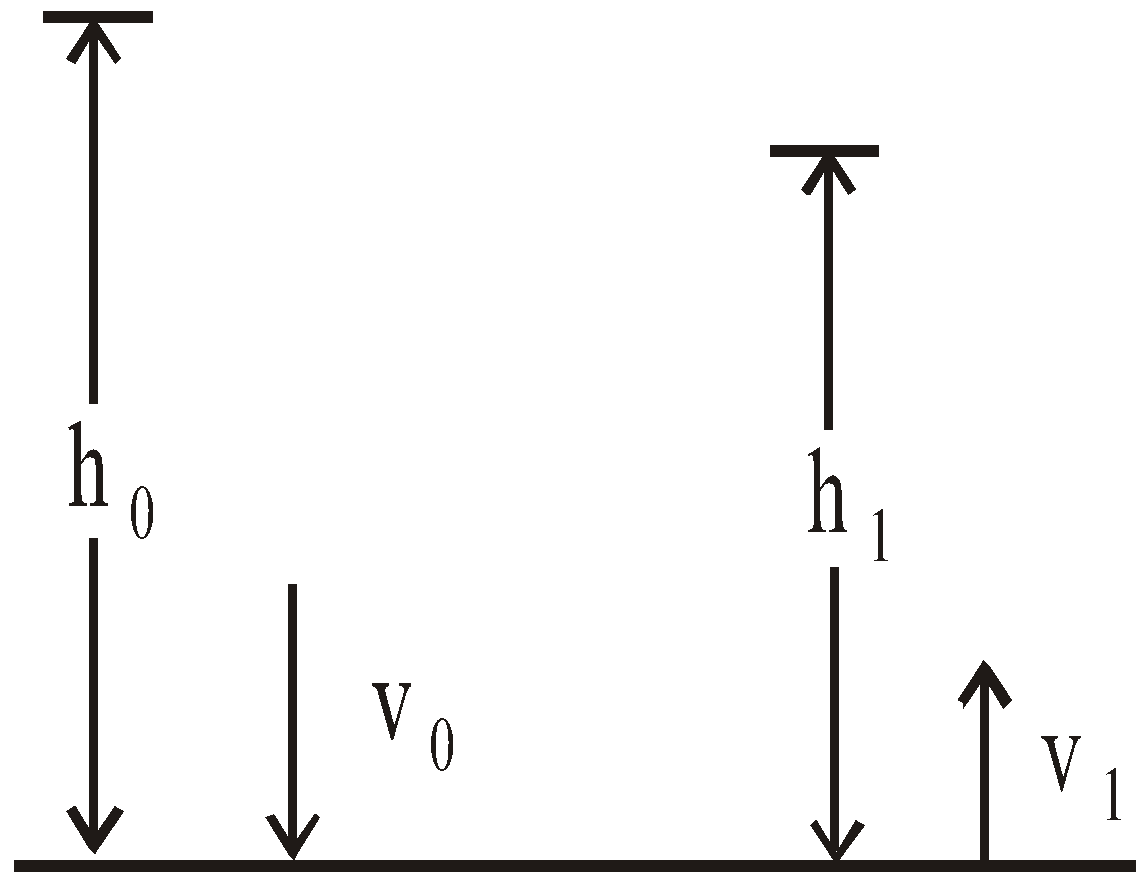
- Suppose, a body is dropped from a height h0 and it strikes the ground with velocity v0. After the (inelastic) collision let it rise to a height h1. If v1 be the velocity with which the body rebounds, then the coefficient of restitution.
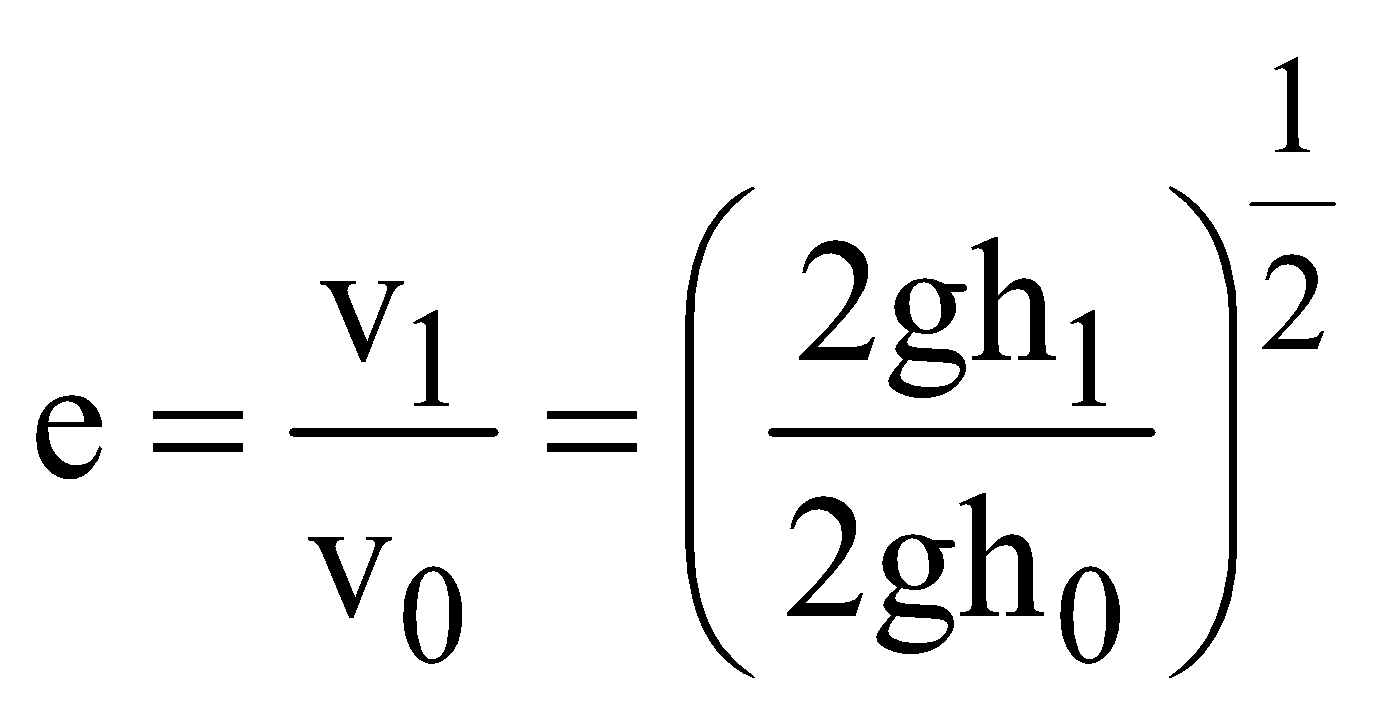 =
= 
- If after n collisions with the ground, the velocity is vn and the height to which it rises be hn, then
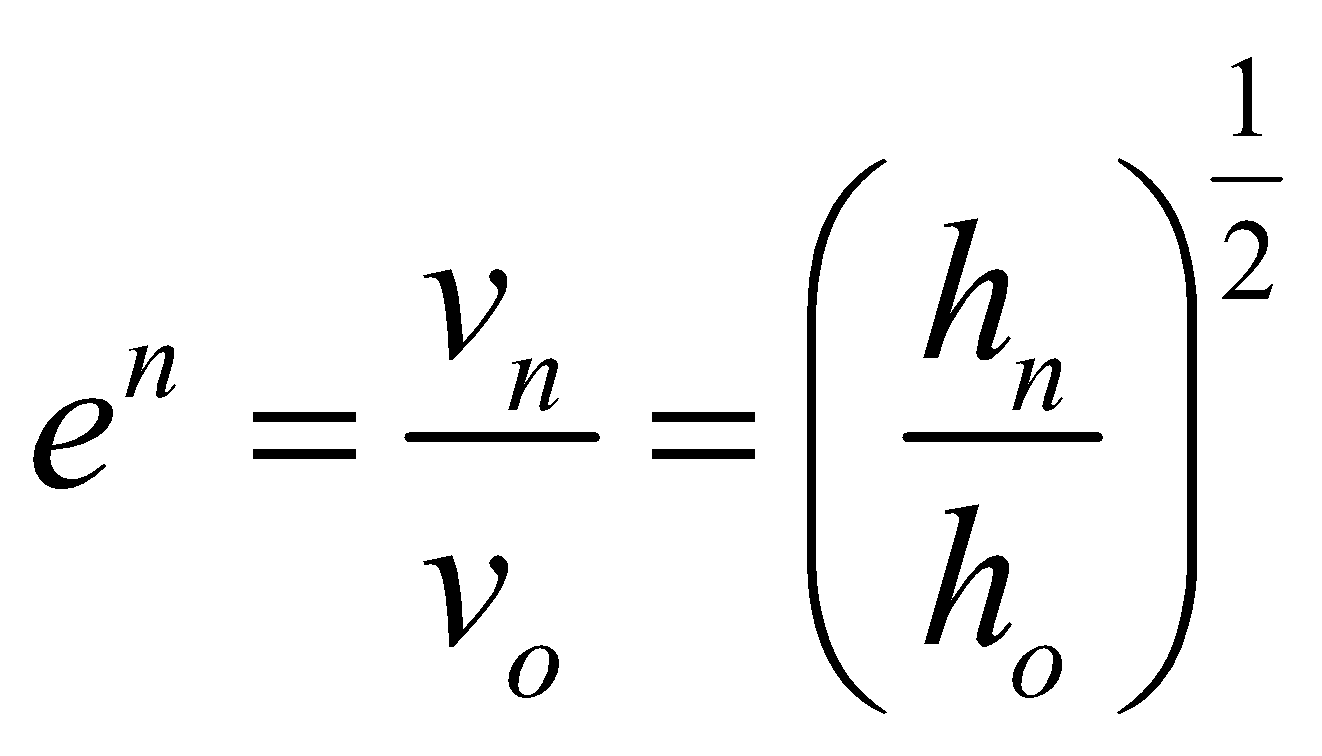
- When a ball is dropped from a height h on the ground, then after striking the ground n times , it rises to a height hn = e2n ho where e = coefficient of restitution.
- If a body of mass m moving with velocity v, collides elastically with a rigid ball, then the change in the momentum of the body is 2 m v.
- If the collision is elastic then we can conserve the energy as
- If two particles having same mass and moving at right angles to each other collide elastically then after the collision they also move at right angles to each other.
- If a body A collides elastically with another body of same mass at rest obliquely, then after the collision the two bodies move at right angles to each other, i.e. (θ + φ) =
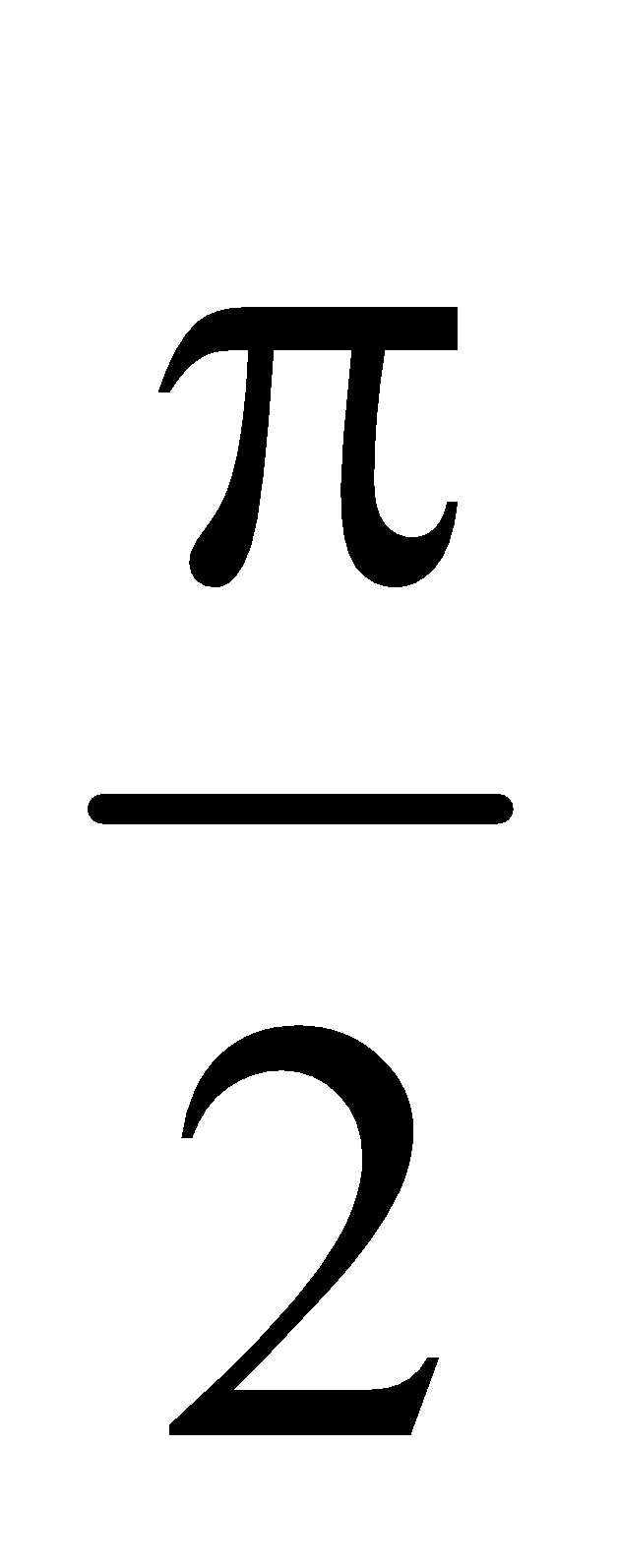
- In an elastic collision of two equal masses, their kinetic energies are exchanged.
- When two bodies collide obliquely, their relative velocity resolved along their common normal after impact is in constant ratio to their relative velocity before impact (resolved along common normal), and is in the opposite direction.