Question
Topic:
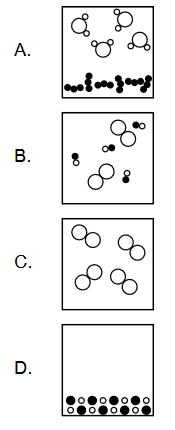
Discuss: Which diagram represents a heterogeneous mixture?
▶️Answer/Explanation
Ans:A
Solution:
A heterogeneous mixture is a mixture that is not uniform throughout, meaning that its components are not evenly distributed and can be visually distinguished. Examples of heterogeneous mixtures include mixtures of sand and water, oil and vinegar, or soil and gravel.
In terms of diagrams, a heterogeneous mixture can be represented by a diagram that shows distinct regions or phases of different components that are visibly separated. For example, a diagram of a mixture of oil and water would show two separate layers with the oil floating on top of the water. Another example would be a diagram of a mixture of sand and water, where the sand particles would settle at the bottom of the container, while the water would remain at the top.
Question
Topic:
Calculate: volume of carbon dioxide, $\mathrm{CO}_2(\mathrm{~g})$, can be obtained by reacting $1 \mathrm{dm}^3$ of methane, $\mathrm{CH}_4(\mathrm{~g})$, with $1 \mathrm{dm}^3$ of oxygen, $\mathrm{O}_2(\mathrm{~g})$ ?
$$
\mathrm{CH}_4(\mathrm{~g})+2 \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{CO}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})
$$
A. $0.5 \mathrm{dm}^3$
B. $1 \mathrm{dm}^3$
C. $2 \mathrm{dm}^3$
D. $6 \mathrm{dm}^3$
▶️Answer/Explanation
Ans:A
Solution:
1. All species discussed are gases: So we can use gas volume directly for calculation.
2. Determine limiting reagent:
For $\mathrm{CH}_4, 1 / 1=1.0 \mathrm{dm}^3 \quad$ For $0_2, 1 / 2=0.5 \mathrm{dm}^3$
Hence, $\mathrm{O}_2$ is the limiting reagent
3. Based on limiting reagent, determine volume of $\mathrm{CO}_2$
V\left(\mathrm{CO}_2\right)=\frac{1}{2} V\left(\mathrm{O}_2\right)=0.5 \mathrm{dm}^3
$$
Question
Topic:
Discuss: the empirical formula of a hydrocarbon with $75 \%$ carbon and $25 \%$ hydrogen by mass?
A. $\mathrm{C}_3 \mathrm{H}$
B. $\mathrm{CH}_2$
C. $\mathrm{C}_2 \mathrm{H}_6$
D. $\mathrm{CH}_4$
▶️Answer/Explanation
Ans:D
Solution:
To determine the empirical formula, we need to find the simplest whole number ratio of atoms in the compound.
Given that the compound has $75 \%$ carbon and $25 \%$ hydrogen by mass, we can assume that we have $75 \mathrm{g}$ of carbon and $25 \mathrm{g}$ of hydrogen in a $100 \mathrm{g}$ sample of the compound.
Next, we need to convert the masses of carbon and hydrogen to moles by dividing by their respective atomic masses:
Number of moles of $\mathrm{C} = \frac{75 \mathrm{g}}{12 \mathrm{g/mol}} = 6.25 \mathrm{mol}$
Number of moles of $\mathrm{H} = \frac{25 \mathrm{g}}{1 \mathrm{g/mol}} = 25 \mathrm{mol}$
Now we need to find the simplest whole number ratio of carbon to hydrogen. To do this, we can divide both the number of moles of carbon and hydrogen by the smallest number of moles:
Divide both sides by $6.25 \mathrm{mol}$:
Number of moles of $\mathrm{C} = 1$
Number of moles of $\mathrm{H} = \frac{25 \mathrm{mol}}{6.25 \mathrm{mol}} = 4$
So the empirical formula of the compound is $\mathrm{CH}_4$. Therefore, the answer is D.
Question
Topic:
Discuss: the ground state electron configuration of an atom of chromium, $\mathrm{Cr}(Z=24) ?$
A. $[\mathrm{Ar}] 3 \mathrm{~d}^6$
B. $[A r] 4 s^2 3 d^4$
C. $[\operatorname{Ar}] 4 \mathrm{~s}^1 3 \mathrm{~d}^5$
D. $[\mathrm{Ar}] 4 \mathrm{~s}^2 4 \mathrm{p}^4$
▶️Answer/Explanation
Ans:C
Solution:
The electron configuration of chromium ($\mathrm{Cr}$) is an exception to the usual filling order of the $3\mathrm{d}$ and $4\mathrm{s}$ orbitals. Chromium has 24 electrons, so its electron configuration based on the Aufbau principle would be:
$1\mathrm{s}^2 2\mathrm{s}^2 2\mathrm{p}^6 3\mathrm{s}^2 3\mathrm{p}^6 4\mathrm{s}^2 3\mathrm{d}^4$
However, it is more stable for chromium to have a half-filled $3\mathrm{d}$ subshell and a singly occupied $4\mathrm{s}$ subshell. Therefore, one electron from the $4\mathrm{s}$ orbital moves to the $3\mathrm{d}$ orbital, giving:
$[\mathrm{Ar}] 4\mathrm{s}^1 3\mathrm{d}^5$
This half-filled $3\mathrm{d}$ subshell is also why the electron configuration of the next element, manganese ($\mathrm{Mn}$), is similarly an exception to the Aufbau principle: $[\mathrm{Ar}] 4\mathrm{s}^2 3\mathrm{d}^5$.
Question
Topic:
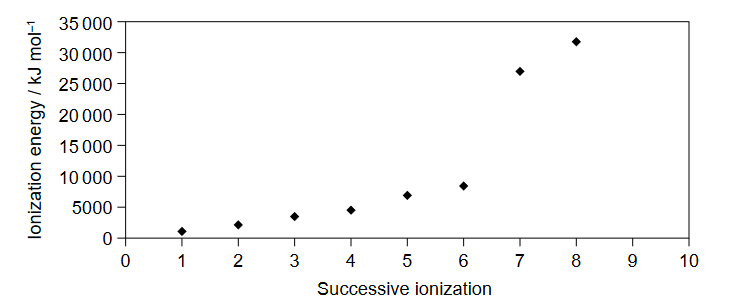
Discuss: Which element is represented by the first eight successive ionization energies on the graph?
A. $\mathrm{Mg}$
B. $\mathrm{S}$
C. $\mathrm{Cl}$
D. $\mathrm{Ar}$
▶️Answer/Explanation
Ans:B
Solution:
The correct answer is B. S (sulfur).
Explanation:
The graph shows the successive ionization energies of an element, which is determined by the energy required to remove each electron from the atom. The first ionization energy is the energy required to remove the first electron, the second ionization energy is the energy required to remove the second electron, and so on.
Looking at the graph, we can see that there are significant increases in ionization energy after the removal of the sixth electron and again after the removal of the seventh electron. This suggests that $\mathrm{IE}: 6$ valence electrons, while $7^{\text {th }}$ electron is removed from inner principal quantum shell.
Based on this information, we can conclude that the element represented by the graph is a Group 16 element, also known as a chalcogen. Among the options given, only sulfur (S) is a Group 16 element.
