Q.1.2020-Nov-Physics_paper_1__TZ0_SL
Topic: Measurements in physics
Discuss: quantity has the same units as those for energy stored per unit volume?
A. Density
B. Force
C. Momentum
D. Pressure
Answer/Explanation
Solution:
$\frac{\text{Energy}}{\text{volume}}$
Unit of energy is same as unit of work ($W=\mathrm{F\cdot s}$) $\Rightarrow [N-m]$
Unit of volume= $m^3$
so ,on dividing $\frac{\mathrm{N}}{m^2}$
Clearly unit of Pressure.
$\colorbox{yellow}{Correct Option-D}$
Q.2.2020-Nov-Physics_paper_1__TZ0_SL
Topic: Vectors and scalars
Given: A list of four physical quantities is
- acceleration
- energy
- mass
- temperature
Calculate: How many scalar quantities are in this list?
A. $1$
B. $2$
C. $3$
D. $4$
Answer/Explanation
A scalar quantity is a physical quantity that has only a magnitude, without any associated direction. From the given list of four physical quantities, mass and temperature are scalar quantities. Acceleration is a vector quantity that has both magnitude and direction, and energy is a scalar quantity that can be either positive or negative.
$\colorbox{yellow}{Correct Option-C}$
Q.3.2021-Nov-Physics_paper_1__TZ0_SL
Topic: Momentum and impulse
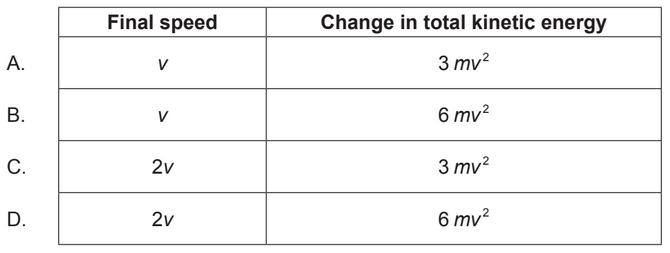
Given: object of mass 2m moving at velocity 3v collides with a stationary object of mass 4m. and objects stick together after the collision.
Calculate: What is the final speed and the change in total kinetic energy immediately after the collision?
Answer/Explanation
Solution:
Momentum ( $\text{mass} \times \text{velocity}$)will be conserved , as no external forces are involve here.
$P_i=P_f$
$\text{2m} \times \text{3v}=\text{(2m+4m)}\times v^{\prime}$
$\boxed{v^{\prime}=\text{v}}$
$\Delta K= (K_f)-(K_i)$
$K_f=\frac{1}{2}\text{(2m+4m)}\times (v^{\prime})^2$
$K_f=\text{3m}\mathrm{v^2}$
$K_i=\frac{1}{2}\text{2m}\times (3v)^2$
$K_i=\text{3m}\mathrm{v^2}$
$\boxed{\Delta K=\text{6m}\mathrm{v^2}}$
$\colorbox{yellow}{Correct Option-D}$
Q.4.2021-Nov-Physics_paper_1__TZ0_SL
Topic: Work, energy and power
Given:An object of mass 1 kg is thrown downwards from a height of 20 m. The initial speed of the object is 6 m/ s , object hits the ground at a speed of 20 m/ s. Assume g = 10 m s–2.
Calculate: best estimate of the energy transferred from the object to the air as it falls?
A. $6 \mathrm{~J}$
B. $18 \mathrm{~J}$
C. $182 \mathrm{~J}$
D. $200 \mathrm{~J}$
Answer/Explanation
Solution:
initial kinetic energy will the estimate of the energy transferred from the object to the air as it falls
$(K_i)=\frac{1}{2}m[(6)^2]$
$(K_i)=\frac{1}{2}\times (1)\times 36= 18 \mathrm{J}$
$\colorbox{yellow}{Correct Option-B}$
