2021-May-Physics_paper_1__TZ1_HL – All Questions with detailed solution
Q.1.2021-May-Physics_paper_1__TZ1_HL
Topic: Uncertainties and errors
Given: Two sets of data, shown below with circles and squares, are obtained in two experiments. The size of the error bars is the same for all points.
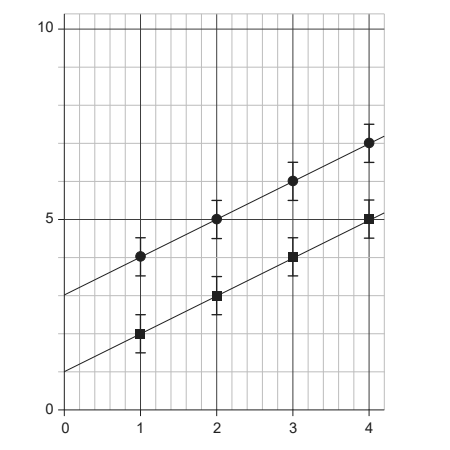
Discuss: What is correct about the absolute uncertainty and the fractional uncertainty of the y intercept of the two lines of best fit?
Answer/Explanation
Solution:
The uncertainty in a measurement can be shown on a graph as an error bar. This bar is drawn above and below the point (or from side to side) and shows the uncertainty in that measurement
The percentage uncertainty in the gradient is given by $=\frac{(m_2)-(m_1)}{m}=\frac{\Delta m}{m} \times 100$.
Q.2.2021-May-Physics_paper_1__TZ1_HL
Topic: Motion
Given: A large stone is dropped from a tall building.
Discuss: What is correct about the speed of the stone after 1 s?
- It is decreasing at increasing rate.
- It is decreasing at decreasing rate.
- It is increasing at increasing rate.
- It is increasing at decreasing rate.
Answer/Explanation
Solution:
Using:$\text{v=u+at}$
here, $u=0$ (dropped from rest) & t=1 sec , $a = g$
As the ball falling on the ground , The velocity will increase as potential energy converted into kinetic. after hitting the ground its velocity will will decrease.
Q.3.2021-May-Physics_paper_1__TZ1_HL
Topic: Motion
Given: The graph shows how the position of an object varies with time in the interval from 0 to 3 s.
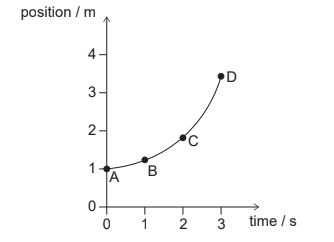
Discuss: At which point does the instantaneous speed of the object equal its average speed over the interval from 0 to 3 s?
Answer/Explanation
Solution:
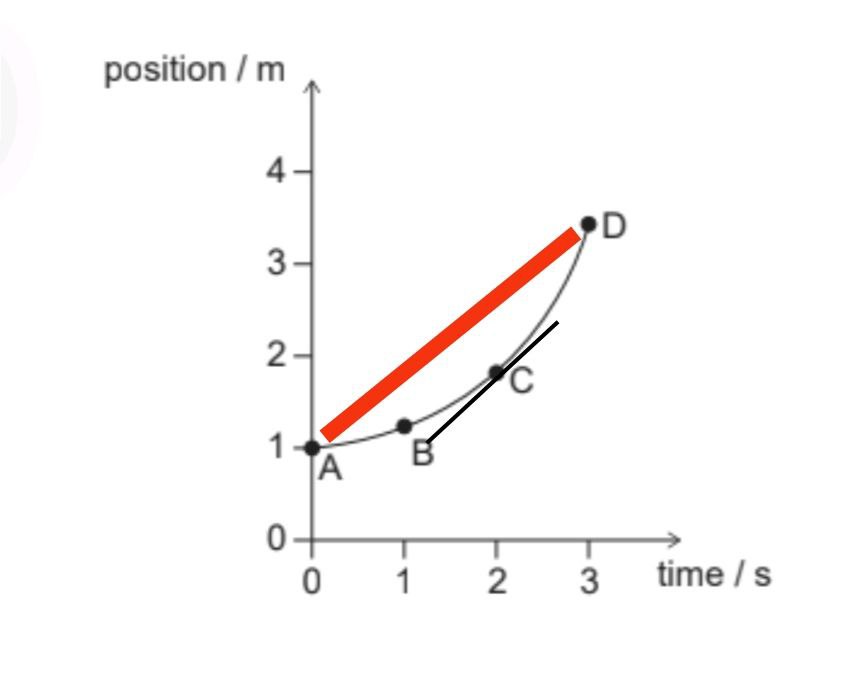
In a graph of position versus time, the instantaneous velocity is the slope of the tangent line at a given point.
The average velocities $=\frac{(x)_f-(x)_i}{(t)_f-(t)_i}$ between times. The slope of line connecting end points (average speed) and slope at C are same.
Q.4.2021-May-Physics_paper_1__TZ1_HL
Topic: Work, energy and power
Given: A car takes 20 minutes to climb a hill at constant speed. The mass of the car is 1200 kg and the car gains gravitational potential energy at a rate of 6.0 kW. Take $ g =10 m/s^2$
Calculate: the height of the hill?
- $0.6 \mathrm{~m}$
- $10 \mathrm{~m}$
- $600 \mathrm{~m}$
- $6000 \mathrm{~m}$
Answer/Explanation
Solution:
Total gains in gravitational potential energy after 20 min.$= \mathrm{6000~W}$
$\text{Enegry}= \text{Power}\times \text{time}$
$\text{Enegry}=6000 \times \text{1200 sec}$
$\text{Enegry}= \mathrm{72}\times \mathrm{10^5}$
$\text{mgh}=\mathrm{72}\times \mathrm{10^5}$
$\mathrm{h}=\frac{\mathrm{72}\times \mathrm{10^5}}{\mathrm{1200} \times \mathrm{10}}$
Q.5.2021-May-Physics_paper_1__TZ1_HL
Topic: Work, energy and power
Given: A mass is released from the top of a smooth ramp of height h. After leaving the ramp, the mass slides on a rough horizontal surface.
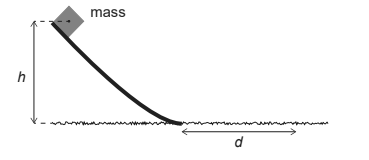
The mass comes to rest in a distance d.
Calculate: the coefficient of dynamic friction between the mass and the horizontal surface?
- $ \frac{g d}{h}$
- $\sqrt{\frac{d}{2 g h}}$
- $\frac{d}{h}$
- $\frac{h}{d}$
Answer/Explanation
Solution:
By using energy conservation.
$\text{mgh}=\text{work done by friction}$
$\text{work done by friction}= \mu \mathrm{mg}\times \text{d}$
