Q.1(a) .2021-May-Physics_paper_2__TZ2_SL
Topic: Momentum and impulse
Given: A football player kicks a stationary ball of mass $0.45 \mathrm{~kg}$ towards a wall. The initial speed of the ball after the kick is $19 \mathrm{~ms}^{-1}$ and the ball does not rotate. Air resistance is negligible and there is no wind.
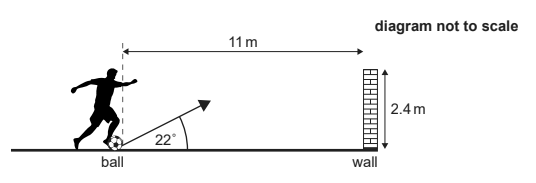
The player’s foot is in contact with the ball for $55 \mathrm{~ms}$.
Calculate: the average force that acts on the ball due to the football player.
Answer/Explanation
Solution:
Average force is the force exerted over a certain period of time. It can be calculated by dividing the total force by the duration of time over which it was exerted.
Mathematically, the average force $F_{\operatorname{avg}}$ is given by:
$$
F_{\operatorname{avg}}=\frac{\Delta \mathrm{p} }{ \Delta t}
$$
where $\Delta \mathrm{p}$ is the change in momentum and $\Delta \mathrm{t}$ is the time interval over which the force is exerted.
$\Delta \mathrm{p}=\text{mass}\times \text{velocity}=0.45 \mathrm{~kg}\times 19 \mathrm{~ms}^{-1}$
$\Delta t=55 \mathrm{~ms}$
$\colorbox{yellow}{$\text{F}=\frac{0.45 \times 19}{0.055} =160 \mathrm{~N}$}$
Q.1[(b) (i)].2021-May-Physics_paper_2__TZ2_SL
Topic: Motion
Given: The ball leaves the ground at an angle of $22^{\circ}$. The horizontal distance from the initial position of the edge of the ball to the wall is $11 \mathrm{~m}$.
Calculate: the time taken for the ball to reach the wall.
Answer/Explanation
Solution:
$\begin{aligned} & \text { horizontal speed }=19 \times \cos 22^{\circ} =17.6 \mathrm{~m} \mathrm{~s}^{-1} \\ & \text { time }= \frac{\text { distance }}{\text { speed }}=\frac{11}{19 \cos 22^{\circ}}= 0.624 \mathrm{~s} \end{aligned}$
$\colorbox{yellow}{time=0.62 s}$
Q.1[(b) (ii)].2021-May-Physics_paper_2__TZ2_SL
Topic: Motion
Given: The top of the wall is $2.4 \mathrm{~m}$ above the ground.
Deduce: whether the ball will hit the wall.
Answer/Explanation
Solution:
First we will calculate the initial vertical speed of the ball and after that will check how much height ball gains in $t=0.624 \mathrm{~s}$
$\text{initial vertical speed}=19 \times \sin 22 ^{\circ}=7.1 \mathrm{~m} \mathrm{~s}^{-1}$
$\text{Height gains by the ball :} = u_y(t)-\frac{1}{2}\times g\times (t)^2$
$7.12 \times (0.624)- \frac{1}{2}\times 9.81 \times (0.624)^2= 2.5 \mathrm{m}$
Clearly height gains by ball is more then the top of the wall ($2.4 \mathrm{~m}$).
$\colorbox{yellow}{ball will not hit the wall}$
Q.1(c).2021-May-Physics_paper_2__TZ2_SL
Topic: Motion
Discuss: In practice, air resistance affects the ball. Outline the effect that air resistance has on the vertical acceleration of the ball. Take the direction of the acceleration due to gravity to be positive.
Answer/Explanation
Solution:
- air resistance opposes direction of motion
- air resistance opposes velocity on the way up vertical acceleration is increased $\text{Or}$ greater than $g$
- air resistance opposes velocity on the way down vertical acceleration is decreased $\text{Or}$ smaller than $g$
Q.1(d).2021-May-Physics_paper_2__TZ2_SL
Topic: Circular motion
Given: The player kicks the ball again. It rolls along the ground without sliding with a horizontal velocity of $1.40 \mathrm{~m} \mathrm{~s}^{-1}$. The radius of the ball is $0.11 \mathrm{~m}$.
Calculate: the angular velocity of the ball. State an appropriate SI unit for your answer.
Answer/Explanation
Solution:
When the ball is rolling without slipping, the linear velocity of any point on the ball’s circumference is equal to the product of the angular velocity of the ball and the radius of the ball.
Thus, we can calculate the angular velocity of the ball using the following formula:
$$
\omega=\frac{v}{r}
$$
where $v$ is the linear velocity of the ball and $r$ is the radius of the ball.
In this case, the linear velocity of the ball is $v = 1.40 \mathrm{~m/s}$ and the radius of the ball is $r = 0.11 \mathrm{~m}$. Substituting these values into the above formula, we get:
$$
\colorbox{yellow}{$\omega=\frac{1.40 \mathrm{~m} / \mathrm{s}}{0.11 \mathrm{~m}} \approx 12.73 \mathrm{rad} / \mathrm{s}$}
$$
Q.2(a).2021-May-Physics_paper_2__TZ2_SL
Topic: Modelling a gas
Given: The graph shows the variation with temperature $T$ of the pressure $P$ of a fixed mass of helium gas trapped in a container with a fixed volume of $1.0 \times 10^{-3} \mathrm{~m}^3$.
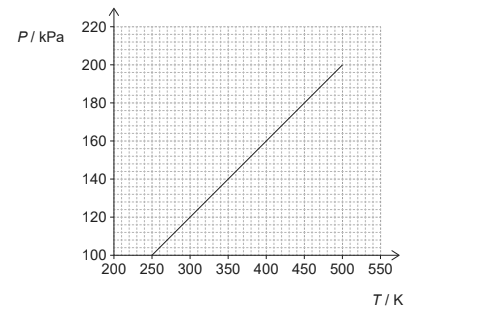
Deduce: whether helium behaves as an ideal gas over the temperature range $250 \mathrm{~K}$ to $500 \mathrm{~K}$.
Answer/Explanation
Solution:
He behaves as ideal gas if $p \propto T$ at constant $V$
$p \propto T$
at $250 \mathrm{~K}$ , $P=100 \mathrm{kPa}$
so, their($\text{p/T}$) ratio will be $\frac{100}{250}=0.4$
Similarly, we will check at $500 \mathrm{~K}$ where $P=200 \mathrm{kPa}$
Ratio will be $\frac{200}{500}=0.4$
$\colorbox{yellow}{From this we can say , $\text{Helium}$ behaves as ideal gas ($p \propto T$)}$
