2022-May-Physics_paper_1__TZ2_HL – All Questions with detailed solution
Q.1.2022-May-Physics_paper_1__TZ2_HL
Topic: Uncertainties and errors
Given: Radius \( =\left ( 10\pm 0.5 \right )cm \)
Calculate: Area of the circle?
A. $(314.2 \pm 0.3) \mathrm{cm}^2$
B. $(314 \pm 1) \mathrm{cm}^2$
C. $(314 \pm 15) \mathrm{cm}^2$
D. $(314 \pm 31) \mathrm{cm}^2$
Answer/Explanation
Solution:
$\begin{aligned} & \text { Area }=\pi r^2=3.14(10)^2=314 \mathrm{~cm} \\ & \frac{\Delta A}{A}=2 \frac{\Delta r}{r} \Delta A=2 \times \frac{0.5}{10} \times 314=\frac{1}{10} \times 314 \Rightarrow \Delta A=31.4 \mathrm{~cm}\end{aligned}$
Q.2.2022-May-Physics_paper_1__TZ2_HL
Topic: Uncertainties and errors
Given: Two different experiments, P and Q, generate two sets of data to confirm the proportionality of variables x and y. The graphs for the data from P and Q are shown. The maximum and minimum gradient lines are shown for both sets of data.
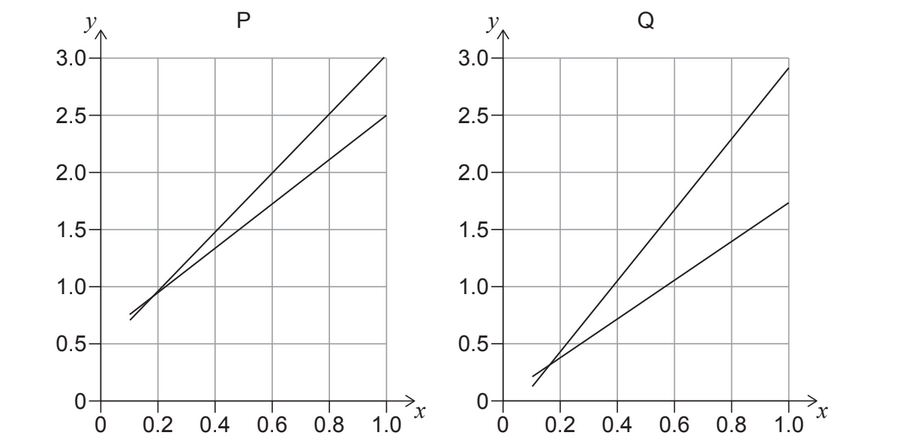
What is true about the systematic error and the uncertainty of the gradient when P is compared to Q?
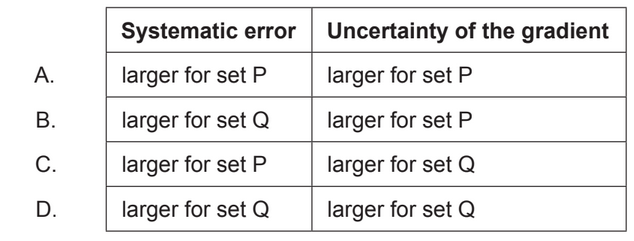
Answer/Explanation
Solution:
Q.3.2022-May-Physics_paper_1__TZ2_HL
Topic: Motion
Given: An object is sliding from rest down a frictionless inclined plane. The object slides 1.0 m during the first second.
Calculate: distance will the object slide during the next second?
A. $1.0 \mathrm{~m}$
B. $2.0 \mathrm{~m}$
C. $3.0 \mathrm{~m}$
D. $4.9 \mathrm{~m}$
Answer/Explanation
Solution:
Let acceleration towards inclined plane is $\text{a}$
$s=u t+\frac{1}{2} a t^2 \quad$ ( here intial velocity,u $=0$ and time, $\mathrm{t}=1 \mathrm{sec}$ )
$
\therefore 1=\frac{1}{2} a(1)^2 a=2 m s^{-2}
$
Distance covered in 2nd second $=u+\frac{a}{2}(2 n-1)=0+\frac{2}{2}(2 \times 2-1)=3 m$
Q.4.2022-May-Physics_paper_1__TZ2_HL
Topic: Motion
Given: A ball is thrown upwards at time t = 0 ,graph shows the variation with time of the height of the ball. The ball returns to the initial height at time T
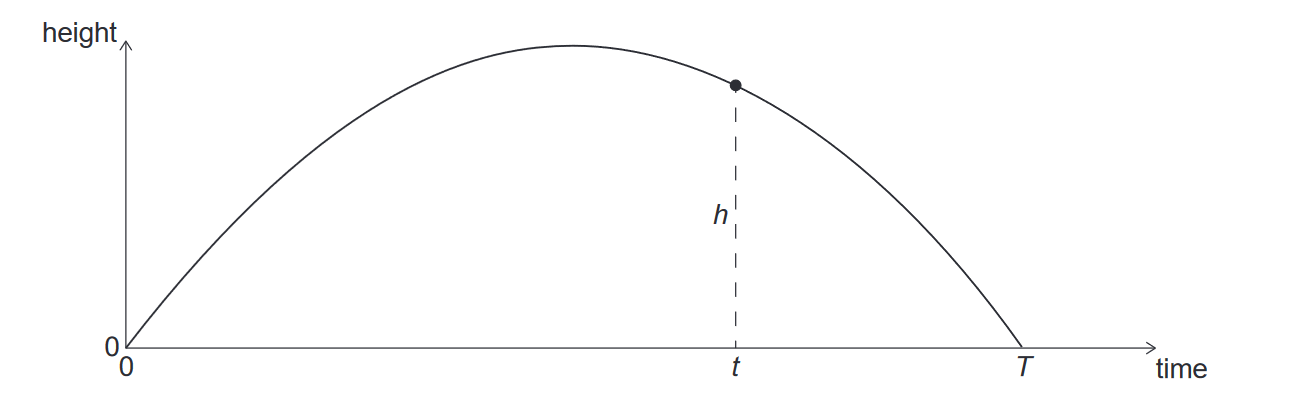
Calculate: height h at time t ?
A. $\frac{1}{2}\mathrm{ g t}^2$
B. $\frac{1}{2} \mathrm{ g t}^2$
C. $\frac{1}{2} \text{g T(T-t)}$
D. $\frac{1}{2} \text{g t(T-t)}$
Answer/Explanation
Solution:
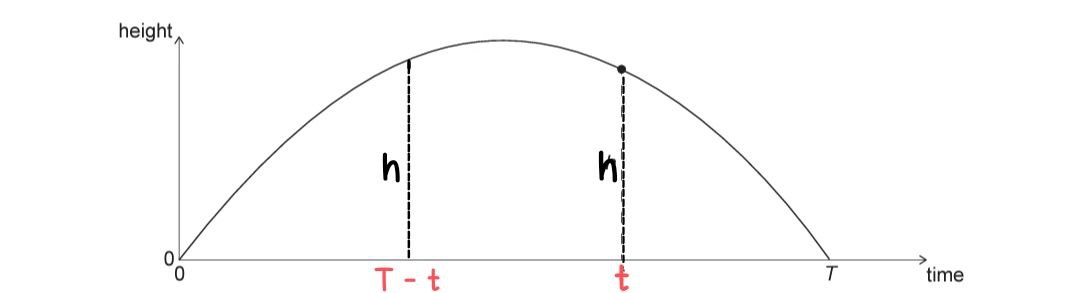
$\begin{aligned} & h=\frac{g t_1 t_2}{2} \\ & t_1=\text { first time when projectile achieve that height from point of projection. } \\ & t_2=\text { second time when it achieve same height. } \\ & \text { g=acceleration due to gravity. } \\ & \text { From graph } \\ & t_1=T-t, t_2=t \\ & h=\frac{1}{2}g t(T-t)\end{aligned}$
Q.5.2022-May-Physics_paper_1__TZ2_HL
Topic: Motion
Given: A solid metal ball is dropped from a tower. The variation with time of the velocity of the ball is plotted.
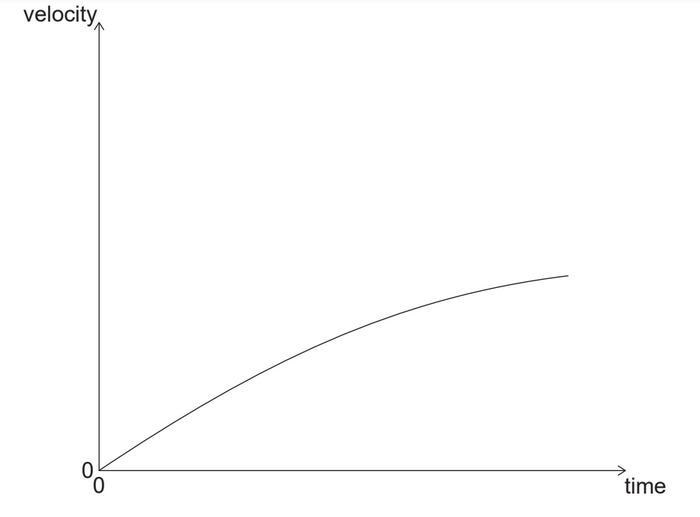
Calculate: A hollow metal ball with the same size and shape is dropped from the same tower. What graph will represent the variation with time of the velocity for the hollow metal ball?
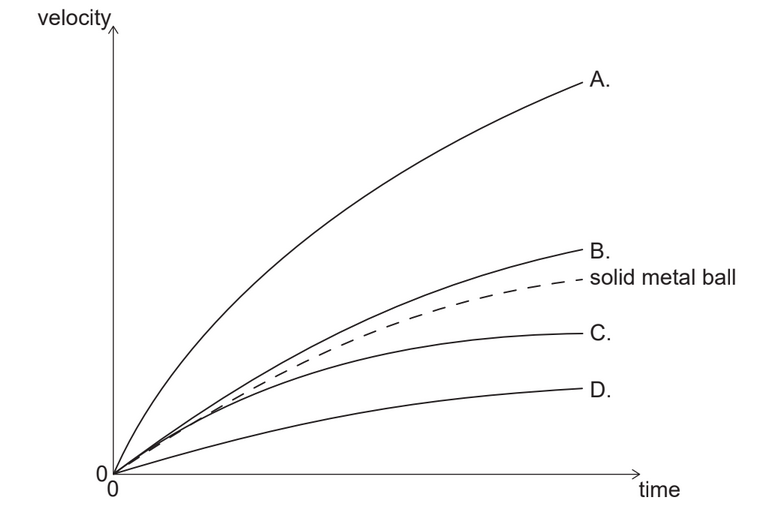
Answer/Explanation
Solution:
