Q.1.2022-May-Physics_paper_1__TZ2_SL
Topic: Uncertainties and errors
Given: Radius \( =\left ( 10\pm 0.5 \right )cm \)
Calculate: Area of the circle?
A. $(314.2 \pm 0.3) \mathrm{cm}^2$
B. $(314 \pm 1) \mathrm{cm}^2$
C. $(314 \pm 15) \mathrm{cm}^2$
D. $(314 \pm 31) \mathrm{cm}^2$
Answer/Explanation
Solution:
$\begin{aligned} & \text { Area }=\pi r^2=3.14(10)^2=314 \mathrm{~cm} \\ & \frac{\Delta A}{A}=2 \frac{\Delta r}{r} \Delta A=2 \times \frac{0.5}{10} \times 314=\frac{1}{10} \times 314 \Rightarrow \Delta A=31.4 \mathrm{~cm}\end{aligned}$
| Area \(=\left ( 314\pm 31.4 \right )~cm \) |
Q.2.2022-May-Physics_paper_1__TZ2_SL
Topic: Uncertainties and errors
Given: Two different experiments, P and Q, generate two sets of data to confirm the proportionality of variables x and y. The graphs for the data from P and Q are shown. The maximum and minimum gradient lines are shown for both sets of data.
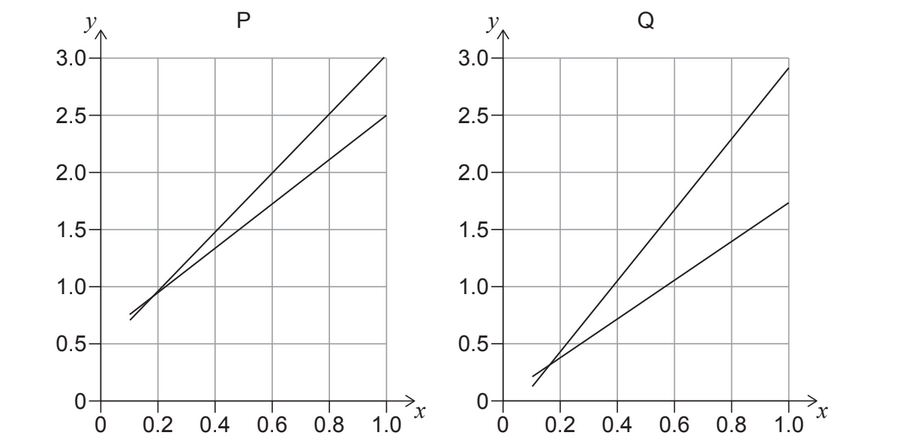
What is true about the systematic error and the uncertainty of the gradient when P is compared to Q?
Answer/Explanation
Solution:
Graph P had a larger y-intercept, meaning a larger systematic error. Graph Q had max/min lines of best fit that were deviated more, this showed larger uncertainty in the gradient.

Q.3.2022-May-Physics_paper_1__TZ2_SL
Topic: Motion
Given: The road from city $X$ to city $Y$ is $1000 \mathrm{~km}$ long. The displacement is $800 \mathrm{~km}$ from $X$ to $Y$.
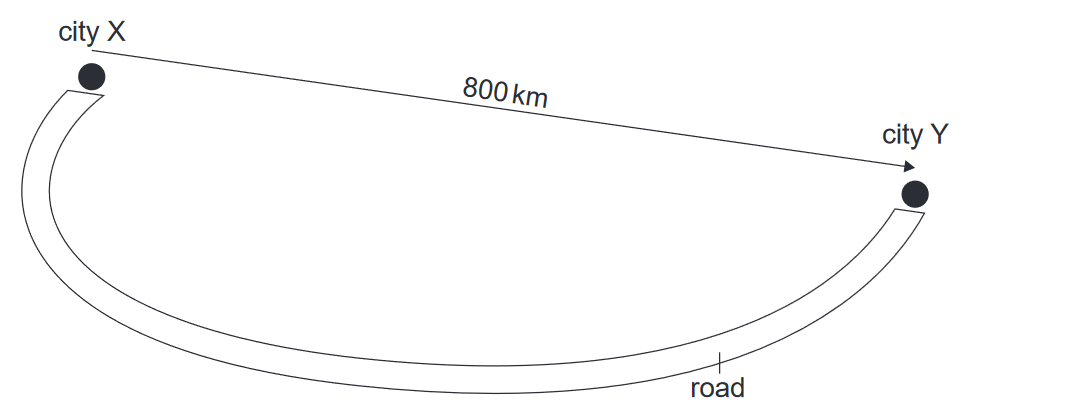
Calculate: What is the distance travelled from $Y$ to $X$ and the displacement from $Y$ to $X$ ?
Answer/Explanation
Solution:
Distance and displacement are both terms used to describe how far an object has moved, but they are different concepts with different meanings in physics.
Distance is a scalar quantity that measures the total length of the path that an object has traveled. It is the actual length of the path traveled by an object irrespective of its direction. It is measured in units of length, such as meters, kilometers, feet, or miles.
Displacement, on the other hand, is a vector quantity that measures the straight-line distance and direction from the starting point to the ending point of an object’s motion. Displacement takes into account only the initial and final positions of an object, not the path it took in between. It is measured in units of length, such as meters, kilometers, feet, or miles, but also includes a direction component, such as north, south, east, or west.
It means distance will be same as of $X$ to $Y$, when person travel $Y$ to $X$ While as displacement will be negative of $X$ to $Y$.

Q.4.2022-May-Physics_paper_1__TZ2_SL
Topic: Motion
Given: A car accelerates uniformly from rest to a velocity $v$ during time $t_1$. It then continues at constant velocity $v$ from $t_1$ to time $t_2$.
Calculate: What is the total distance covered by the car in $t_2 ?$
A. $vt_2$
B. $\frac{1}{2} v\left(t_2-t_1\right)+v t_1$
C. $\frac{1}{2} v\left(t_2+t_1\right)$
D. $\frac{1}{2} v t_1+v\left(t_2-t_1\right)$
Answer/Explanation
Solution:
Using $\text{v=u+at}$
u= initial velocity =0 (at rest)
$\mathrm{v}=0+\mathrm{a}\times \mathrm{t}_1$
$a=\frac{\mathrm{v}}{\mathrm{t}_1}$
Let the distance cover in $\mathrm{t}_1$ time is $\mathrm{s}_1$
$\mathrm{s}_1=\mathrm{ut}+\frac{1}{2}\mathrm{a}(\mathrm{t}_1)^2$
$
\begin{aligned}
&\mathrm{s}_1=\frac{1}{2}\left(\frac{\mathrm{v}}{\mathrm{t}_1}\right)\left(\mathrm{t}_1\right)^2 \\
&\mathrm{s}_1=\frac{1}{2}\mathrm{v}\mathrm{t}_1
\end{aligned}
$
Now,
After gaining velocity $\text{v}$ car is moving with constant speed from $t_1$ to time $t_2$, so acceleration will be zero.
Let the distance covered in this time period is $\mathrm{s}_1$
$\mathrm{s}_1=\mathrm{v}\times (\mathrm{t}_2-\mathrm{t}_1)$ [$\text{using: distance=speed}\times \text{time}$]
So total distance will be $\mathrm{s}_1+\mathrm{s}_2$
$\text{Total distance}=\frac{1}{2}\mathrm{v}\mathrm{t}_1+\mathrm{v}\cdot (\mathrm{t}_2-\mathrm{t}_1)$

