Question-1(a) :2022-nov-Chemistry_paper_2__TZ0_SL
Topic:
Given: Ammonium nitrate, $\mathrm{NH}_4 \mathrm{NO}_3$, is used as a high nitrogen fertilizer.
Calculate: the percentage by mass of nitrogen in ammonium nitrate. Use section 6 of the data booklet.
Answer/Explanation
Solution:
The molar mass of ammonium nitrate is:
$\mathrm{Molar \ mass \ of \ NH_4NO_3} = 14.01 \times 2 + 1.01 \times 4 + 16.00 \times 3 = 80.04 \ \mathrm{g/mol}$
The molar mass of nitrogen in ammonium nitrate is:
$\mathrm{Molar \ mass \ of \ N} = 14.01 \ \mathrm{g/mol}$
Therefore, the percentage by mass of nitrogen in ammonium nitrate is:
$\mathrm{% \ N} = \frac{\mathrm{Molar \ mass \ of \ N}}{\mathrm{Molar \ mass \ of \ NH_4NO_3}} \times 100%$
$\mathrm{% \ N} = \frac{2 \times 14.01 \mathrm{~g} \mathrm{~mol}^{-1}}{\left(2 \times 14.01 \mathrm{gmol}^{-1}+4 \times 1.01 \mathrm{gmol}^{-1}+3 \times 16.00 \mathrm{gmol}^{-1}\right)} \times 100 %$
$\mathrm{% \ N} = \frac{28.02 \mathrm{~g} \mathrm{~mol}^{-1}}{80.04 \mathrm{~g} \mathrm{~mol}^{-1}} \times 100 %$
$\mathrm{% \ N} = 0.3496 \times 100 % \approx 35.00 %$
Therefore, the percentage by mass of nitrogen in ammonium nitrate is approximately 35.00%.
Question-1 (b) :2022-nov-Chemistry_paper_2__TZ0_SL
Topic:
Discuss: with a reason, whether the ammonium ion is a Brønsted-Lowry acid or base.
Answer/Explanation
Solution:
For example, when ammonium ion reacts with water, it donates a proton to the water molecule to form hydronium ion and ammonia:
$\mathrm{NH_4^+ + H_2O \rightarrow H_3O^+ + NH_3}$
In this reaction, ammonium ion acts as an acid (donating a proton) and water molecule acts as a base (accepting a proton). Therefore, the ammonium ion is a Brønsted-Lowry acid.
Question-1 (c) :2022-nov-Chemistry_paper_2__TZ0_SL
Topic:
Discuss: the Lewis (electron dot) structure for the nitrate anion.
Answer/Explanation
Solution:
The Lewis structure of a nitrate $\left[\mathrm{NO}_3\right]^{-}$ion consists of a nitrogen $(\mathrm{N})$ atom and three oxygen $(0)$ atoms. The nitrogen $(\mathrm{N})$ atom is present at the center of the molecular ion, while three oxygen (0) atoms occupy terminal positions, one on each side.
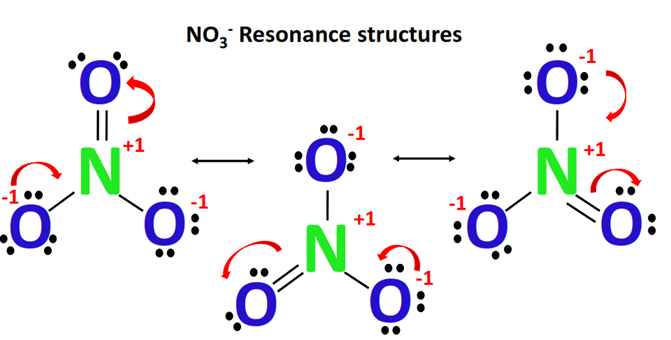
There are a total of 3 electron density regions around the central $\mathrm{N}$-atom in the Lewis structure of $\left[\mathrm{NO}_3\right]^{-}$. All 3 electron density regions or electron domains are constituted of $\mathrm{N}=\mathrm{O}$ and $\mathrm{N}-\mathrm{O}$ bond pairs. Thus, there is no lone pair on the central $\mathrm{N}$-atom in $\mathrm{NO}_3^{-}$ Lewis dot structure.
$\mathrm{NO}_3{ }^{-}$ Molecular Geometry And Bond Angles:
In nitrate, there is one central atom which is surrounded by three identically-bonded oxygen atoms which lie at the corners of a triangle and at the same onedimensional plane. In essence, nitrate has 3 electron domains and no lone pairs. Therefore, $\mathrm{NO}_3^{-}$molecular geometry is slightly bent and is trigonal planar. The bond angle is $120^{\circ}$.
Question-1(d) :2022-nov-Chemistry_paper_2__TZ0_SL
Topic:
Given: $\mathrm{A} 0.20 \mathrm{~mol} \mathrm{dm}^{-3}$ solution of ammonium nitrate is prepared.
Calculate: the $\mathrm{pH}$ of an ammonium nitrate solution with $\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=1.07 \times 10^{-5} \mathrm{~mol} \mathrm{dm}^{-3}$. Use section 1 of the data booklet.
Answer/Explanation
Solution:
The concentration of $\mathrm{H_3O^+}$ is given as $1.07 \times 10^{-5}$ mol/dm$^3$.
Using the equilibrium constant expression and the concentrations of $\mathrm{H_3O^+}$ and $\mathrm{NH_4^+}$, we can solve for the concentration of $\mathrm{NH_3}$:
$K_\mathrm{a} = \dfrac{[\mathrm{H_3O^+}][\mathrm{NH_3}]}{[\mathrm{NH_4^+}]}$
$4.8 \times 10^{-10} = \dfrac{(1.07 \times 10^{-5})[\mathrm{NH_3}]}{(0.20)}$
$[\mathrm{NH_3}] = 2.56 \times 10^{-7}~\mathrm{mol/dm^3}$
The $\mathrm{pH}$ of the solution can be calculated using the concentration of hydronium ions, $\mathrm{H_3O^+}$, as follows:
$\mathrm{pH} = -\log([\mathrm{H_3O^+}])$
$\mathrm{pH} = -\log(1.07 \times 10^{-5})$
$\mathrm{pH} = 4.97$
Therefore, the $\mathrm{pH}$ of the ammonium nitrate solution is 4.97.
Question-1[(e) (i)] :2022-nov-Chemistry_paper_2__TZ0_SL
Topic:
Given: Cold packs contain ammonium nitrate and water separated by a membrane.
The mass of the contents of the cold pack is $25.32 \mathrm{~g}$ and its initial temperature is $25.2^{\circ} \mathrm{C}$. Once the contents are mixed, the temperature drops to $0.8^{\circ} \mathrm{C}$.
Calculate: the energy, in $\mathrm{J}$, absorbed by the dissolution of ammonium nitrate in water within the cold pack. Assume the specific heat capacity of the solution is $4.18 \mathrm{~J} \mathrm{~g}^{-1} \mathrm{~K}^{-1}$. Use section 1 of the data booklet.
Answer/Explanation
Solution:
To calculate the energy absorbed by the dissolution of ammonium nitrate in water within the cold pack, we can use the equation:
$q = mc \Delta T$
where $q$ is the energy absorbed (in J), $m$ is the mass of the solution (in g), $c$ is the specific heat capacity of the solution (in J g$^{-1}$ K$^{-1}$), and $\Delta T$ is the change in temperature (in K).
Using the given values and the hint provided, we get:
$q = 25.32 \mathrm{~g} \times 4.18 \mathrm{~J} \mathrm{~g}^{-1} \mathrm{~K}^{-1} \times (25.2^{\circ} \mathrm{C} – 0.8^{\circ} \mathrm{C}) = 2580 \mathrm{~J}$
Therefore, the energy absorbed by the dissolution of ammonium nitrate in water within the cold pack is 2580 J.
Question-1[(e) (ii)] :2022-nov-Chemistry_paper_2__TZ0_SL
Topic:
Calculate: the mass of ammonium nitrate in the cold pack using your answer obtained in (d)(i) and sections 6 and 19 of the data booklet.
If you did not obtain an answer in (d)(i), use $3.11 \times 10^3 \mathrm{~J}$, although this is not the correct answer.
Answer/Explanation
Solution:
To determine the mass of ammonium nitrate in the cold pack, we can use the enthalpy change of dissolution and the mass of water present in the cold pack.
From part (i), we found that the energy absorbed by the dissolution of ammonium nitrate in water within the cold pack is $2580\mathrm{J}$. Using section 6 of the data booklet, we can find the enthalpy change of dissolution for ammonium nitrate to be $25.69\mathrm{kJ ~mol^{-1}}$.
Therefore, the number of moles of ammonium nitrate that dissolved can be calculated as:
$$
n=\frac{\Delta H}{\Delta H^0}=\frac{2580 \mathrm{~J} \times \frac{1 \mathrm{~kJ}}{100 \mathrm{0}~ J}}{25.69 \mathrm{kJ}~ \mathrm{mol}^{-1}}=0.100 \mathrm{~mol}
$$
Using the molar mass of ammonium nitrate from section 19 of the data booklet, which is $80.06\mathrm{g~mol^{-1}}$, we can find the mass of ammonium nitrate present in the cold pack:
$$
m=n \times M=0.100 \mathrm{~mol} \times 80.06 \mathrm{~g} \mathrm{~mol}^{-1}=8.01 \mathrm{~g}
$$
Therefore, the mass of ammonium nitrate in the cold pack is $8.01\mathrm{~g}$.
Question-1[(e) (iii)] :2022-nov-Chemistry_paper_2__TZ0_SL
Topic:
Given: The absolute uncertainty in mass of the contents of the cold pack is $\pm 0.01 \mathrm{~g}$ and in each temperature reading is $\pm 0.2^{\circ} \mathrm{C}$. Using your answer in (d)(ii),
Calculate: the absolute uncertainty in the mass of ammonium nitrate in the cold pack.
If you did not obtain an answer in (d)(ii), use $6.55 \mathrm{~g}$, although this is not the correct answer.
Answer/Explanation
Solution:
To calculate the absolute uncertainty in the mass of ammonium nitrate in the cold pack, we need to use the formula for fractional uncertainty and multiply it by the value of mass of ammonium nitrate:
fractional uncertainty in $m=\frac{\text { absolute uncertainty in } m}{\text { value of } m}$
Using the values given in the question, we can calculate the fractional uncertainty in mass as follows:
fractional uncertainty in $m=\frac{0.01 \mathrm{~g}}{25.32 \mathrm{~g}} \times 100 \% \approx 0.04 \%$
We can also calculate the fractional uncertainty in temperature as follows:fractional uncertainty in $\Delta T=\frac{0.2^{\circ} \mathrm{C}}{24.4^{\circ} \mathrm{C}} \times 100 \% \approx 0.82 \%$
Since the fractional uncertainty in mass is much smaller than the fractional uncertainty in temperature, we can assume that the uncertainty in mass is negligible compared to the uncertainty in temperature.
Therefore, we can estimate the absolute uncertainty in mass of ammonium nitrate as follows:
absolute uncertainty in mass of ammonium nitrate $\approx 2 \% \times 8.01 \mathrm{~g}=0.2 \mathrm{~g}$
Therefore, the absolute uncertainty in the mass of ammonium nitrate in the cold pack is $0.2 \mathrm{~g}$.
