Question
A sphere of radius 2.1mm falls with terminal (constant) velocity through a liquid, as shown in Fig. 1.1.
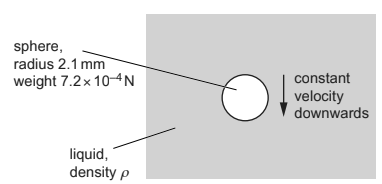
Fig. 1.1
Three forces act on the moving sphere. The weight of the sphere is \(7.2\times 10^{-4}N\) and the upthrust acting on it is \(4.8\times 10^{-4}N\). The viscous force \(F_{V}\) acting on the sphere is given by
\(F_{V} = krv\)
where \(r\) is the radius of the sphere, \(v\) is its velocity and \(k\) is a constant. The value of \(k\) in SI units is \(17\).
(a) Determine the SI base units of \(k\).
(b) Use the value of the upthrust acting on the sphere to calculate the density \(ρ\) of the liquid.
(c) (i) On the sphere in Fig. 1.1, draw three arrows to show the directions of the weight W, the upthrust U and the viscous force \(F_{V}\). Label these arrows W, U and \(F_{V}\) respectively.
(ii) Determine the magnitude of the terminal (constant) velocity of the sphere.
Answer/Explanation
Ans:

Question
Water leaves the end of a hose pipe at point P with a horizontal velocity of 6.6m/s, as shown in fig.2.1
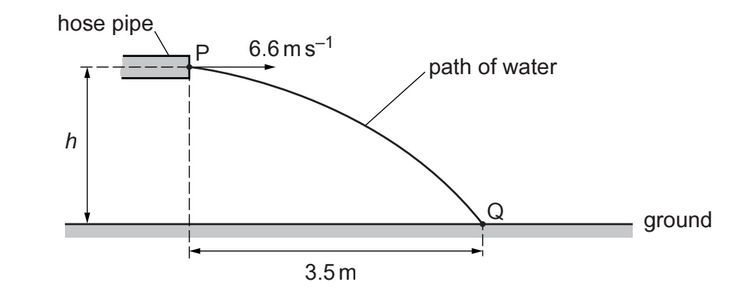
Point P is at height h above the ground. The water hits the ground at point Q. The horizontal distance from P to Q is 3.5m. Air resistance is negligible. Assume that the water between P and Q consists of non-interacting droplets of water and that the only force acting on each droplet is its weight.
(a) Explain, briefly, why the horizontal component of the velocity of a droplet of water remains constant as it moves from P to Q.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………… [1]
(b) Show that the time taken for a droplet of water to move from P to Q is 0.53s.[1]
(c) Calculate height h.
h = ………………………………………………m [2]
(d) For the movement of a droplet of water from P to Q, state and explain whether the
displacement of the droplet is less than, more than or the same as the distance along its path.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………… [1]
(e) Calculate the magnitude of the displacement of a droplet of water that moves from P to Q.
displacement = ………………………………………………m [2] [Total: 7]
Answer/Explanation
Ans:
(a) force (on droplet of water) in horizontal direction is zero.
(b) (time taken =) 3.5 / 6.6 = 0.53 (s)
(c) s = ut + 1⁄2\(at^ 2\)
s = 1⁄2× 9.81× 0.532 \(\rightarrow h = 1.4 m\)
(d) displacement is straight-line distance (from P to Q) so less (than distance along path)
or
displacement is the shortest distance (from P to Q).
(e) \((displacement)^2 = 3.5^2 + 1.4^2\)
displacement = 3.8 m
Question
A jet of water hits a vertical wall at right angles, as shown in Fig. 3.1.
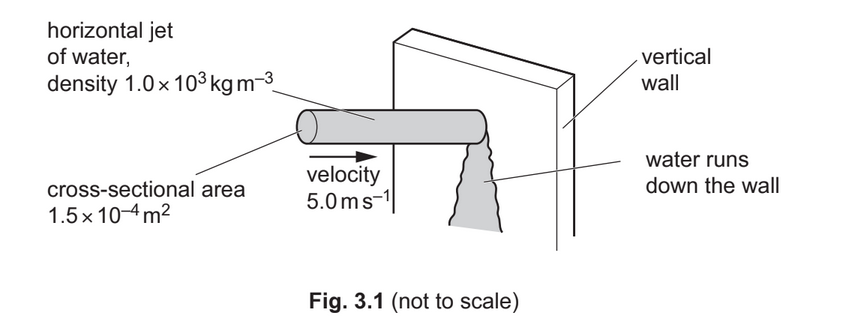
The water hits the vertical wall with a velocity of 5.0m/s in a horizontal direction. The cross-sectional area of the jet is \(1.5 \times 10^{–4}m^2\). The density of the water is \(1.0 \times 10^3 kg m^{–3}\).
The water runs down the wall after hitting it.
(a) Show that, over a time of 1.6s, the mass of water hitting the wall is 1.2kg.
[2]
(b) Calculate:
(i) the decrease in the horizontal momentum of the mass of water in (a) due to hitting the wall
decrease in momentum = ……………………………………………. Ns [1]
(ii) the magnitude of the horizontal force exerted on the water by the wall.
force = ……………………………………………… N [1]
(c) State and explain the magnitude of the horizontal force exerted on the wall by the water.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………… [1]
(d) Calculate the pressure exerted on the wall by the water.
pressure = ……………………………………………. Pa [2]
[Total: 7]
Answer/Explanation
Ans:
(a) \((m =) \rho V\)
\(= 1.0 \times 10^3 \times 1.5 x 10^{-4} \times 5.0 \times 1.6 = 1.2 (kg)\)
(b)(i) \((\Delta )p = 1.2 \times 5.0\)
\(= 6.0 N s\)
(b)(ii) F = 6.0/1.6 or \(1.2 \times 5.0/1.6\)
= 3.8 N
(c) Newton’s third law applies (so) 3.8 N.
(d) p = F/A
\(= 3.8/1.5 \times 10^{-4}\)
\(= 2.5 \times 10^4 \)Pa
Question
A child moves down a long slide, as shown in Fig. 4.1.
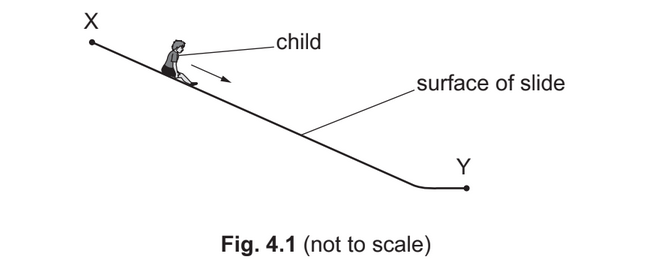
The child moves from rest at the top end X of the slide. An average resistive force of 76N opposes the motion of the child as they move to the lower end Y of the slide. The kinetic energy of the child
at Y is 300J. The decrease in gravitational potential energy of the child as it moves from X to Y is 3200J.
(a) Determine the ratio ![]()
ratio = ………………………………………………… [1]
(b) Use the answer in (a) to calculate the ratio ![]()
ratio = ………………………………………………… [2]
(c) Calculate the length of the slide from X to Y.
length = ………………………………………………m [2]
(d) At end Y of the slide, the child is brought to rest by a board, as shown in Fig. 4.2.
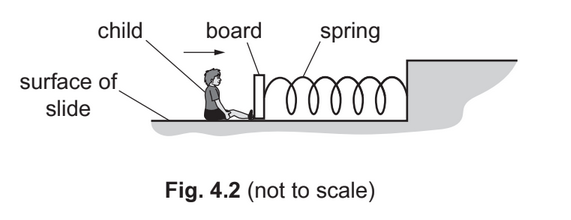
A spring connects the board to a fixed point. The spring obeys Hooke’s law and has a spring constant of 63Nm–1. The child hits the board so that it moves to the right and compresses the
spring. The speed of the child becomes zero when the elastic potential energy of the spring has increased to its maximum value of 140J.
(i) Calculate the maximum compression of the spring.
maximum compression = ………………………………………………m [2]
(ii) Calculate the percentage efficiency of the transfer of the kinetic energy of the child to the elastic potential energy of the spring.
percentage efficiency = …………………………………………….. % [1]
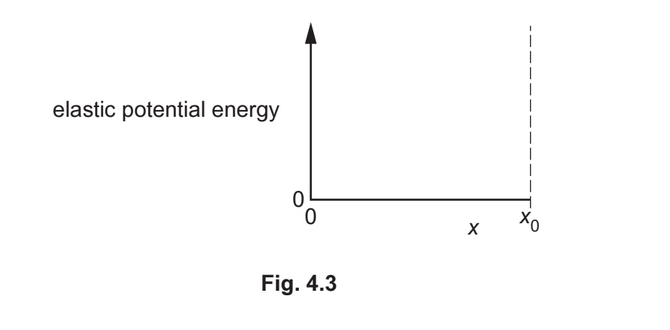
(iii) The maximum compression of the spring is \(x_0\). On Fig. 4.3, sketch a graph to show the variation of the elastic potential energy of the spring with its compression x from x = 0 to
\(x = x_0\). Numerical values are not required.
Answer/Explanation
Ans:
(a)ratio = 300 / 3200
= 0.094
(b)\(E= 1/2mv^ 2\) or E∝ \(v^ 2\)
ratio \(= (0.094)^{0.5}\)
= 0.31
(c) work (done against frictional force) = 3200– 300 (=2900)
length = 2900 / 76 = 38 m

(d)(ii) percentage efficiency = (140 / 300) × 100
= 47%
(d)(iii) curved line from the origin
gradient of line increases
Question
(a) (i) State the conditions required for the formation of a stationary wave.
……………………………………………………………………………………………. [2]
(ii) State the phase difference between any two vibrating particles in a stationary wave between two adjacent nodes.
phase difference = ………………………………………………..° [1]
(b) A motorcycle is travelling at 13.0 m/s along a straight road. The rider of the motorcycle sees a pedestrian standing in the road directly ahead and operates a horn to emit a warning sound.
The pedestrian hears the warning sound from the horn at a frequency of 543Hz. The speed of the sound in the air is 334 m/s.
(i) Calculate the frequency, to three significant figures, of the sound emitted by the horn.
frequency = ……………………………………………. Hz [2]
(ii) The motorcycle rider passes the stationary pedestrian and then moves directly away from her. As the rider moves away, he operates the horn for a second time. The pedestrian now hears sound that is increasing in frequency.
State the variation, if any, in the speed of the motorcycle when the rider operates the horn for the second time…………………………………… [1]
(c) A beam of vertically polarised monochromatic light is incident normally on a polarising filter, as shown in Fig. 5.1.
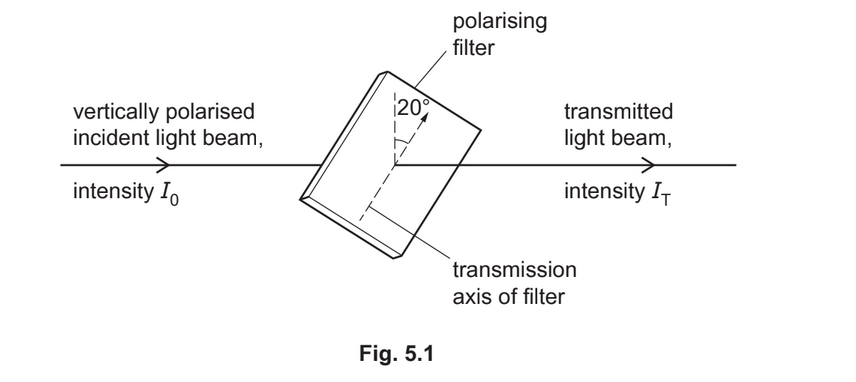
The filter is positioned with its transmission axis at an angle of 20° to the vertical. The incident light has intensity \(I_0\) and the transmitted light has intensity \(I_T\).
(i) By considering the ratio \(\frac{I_T}{I_0}\) calculate the ratio 
Show your working. ratio = ………………………………………………… [3]
(ii) The filter is now rotated, about the direction of the light beam, from its starting position shown in Fig. 5.1. The direction of rotation is such that the angle of the transmission axis to the vertical initially increases.
Calculate the minimum angle through which the filter must be rotated so that the intensity of the transmitted light returns to the value that it had when the filter was at its starting position.
angle = ………………………………………………. ° [1]
Answer/Explanation
Ans:
(a)(i) (two) waves travelling (at same speed) in opposite directions overlap waves (of the same type) have same frequency/wavelength
(a)(ii) phase difference = 0

Question
The ends of a metal resistance wire are connected to a battery of electromotive force (e.m.f.) 8.0V and negligible internal resistance, as shown in Fig. 6.1.
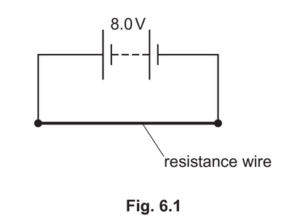
The power dissipated by the resistance wire is 36W.
(a) Calculate:
(i) the current in the resistance wire
current = ……………………………………………….A [2]
(ii) the number of free electrons that pass through the resistance wire in a time of 50s
number = ………………………………………………… [2]
(iii) the resistance of the wire.
resistance = ……………………………………………… Ω [2]
(b) The metal of the resistance wire in the circuit has a resistivity of \(1.4 \times 10–^{6}\) Ω-m. The cross-sectional area of the wire is 0.25 \(mm^2\).
Determine the length of the wire.
length = ………………………………………………m [2]
(c) The circuit shown in Fig. 6.1 is modified by replacing the original resistance wire with a second resistance wire. The second wire has a greater diameter than the original wire. There are no
other differences between the second wire and the original wire. By reference to resistance, state and explain whether the power dissipated by the second wire is more than, less than or the same as the power dissipated by the original wire.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………… [2]
(d) The circuit shown in Fig. 6.1 is modified by connecting a second battery, of e.m.f. 8.0V and negligible internal resistance, in parallel with the original battery and the original resistance
wire, as shown in Fig. 6.2.
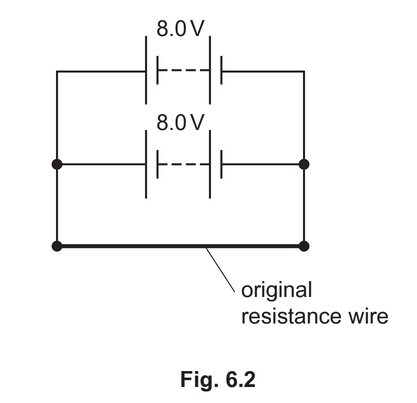
By reference to the current in the resistance wire, state and explain whether the addition of the second battery causes the power in the original resistance wire to decrease, increase or stay the same.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………… [2]
[Total: 12]
Answer/Explanation
Ans:
(a)(i)
\(P =VI\)
\(I = 36 / 8.0 = 4.5A\)
(a)(ii) charge = 4.5× 50 = 225
number \(= 225 / 1.6 × 10^{–19}\)
\(= 1.4 × 10^{21}\)
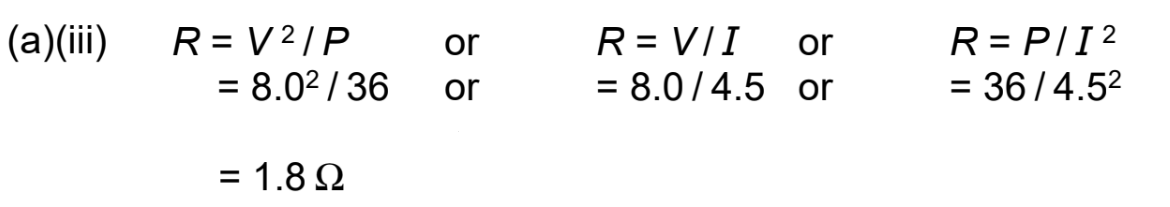
(b) \(R = ρL / A\)
\(L = (1.8 × 0.25 × 10^{–6}) / 1.4 × 10^{–6} = 0.32 m\)
(c) (larger cross-sectional area, same length, same resistivity and so) less resistance (same p.d. and more current so) more power (dissipated)
(d) current (in wire) is the same (same p.d. across wire so) power stays the same
Question
(a) A nucleus of sodium-22 ![]() decays by emitting a \(β^+\) particle. A different nucleus is formed by the decay.
decays by emitting a \(β^+\) particle. A different nucleus is formed by the decay.
(i) State the name of another lepton that is produced by the decay.
…………………………………………………………….. [1]
(ii) Determine the nucleon number and the proton number of the nucleus that is formed by the decay.
nucleon number = ………………………………………………………
proton number = ………………………………………………………
[2]
(iii) The quark composition of a nucleon in the sodium-22 nucleus is changed during the decay.
Describe the change to the quark composition of the nucleon.
………………………………………………………………………………
……………………………………………………………………………………… [1]
(b) A baryon consists of quarks that are the same flavour (type). The charge of the baryon is –2e, where e is the elementary charge.
(i) Calculate, in terms of e, the charge of each quark.
charge = ……………………………………………… e [1]
(ii) State a possible flavour (type) of the quarks.
………………………………………………………. [1]
[Total: 6]
Answer/Explanation
Ans:
(a)(i) (electron) neutrino
(a)(ii) nucleon number = 22
proton number = 10
(a)(iii) up up down changes to up down down or up changes to down
(b)(i) charge = – 2⁄3e
(b)(ii) antiup / anticharm / antitop
