Question
(a) Use an expression for work done, in terms of force, to show that the SI base units of energy are kg\(m^2 s^{–2}\).
(b) (i) The energy E stored in an electrical component is given by
\(E=\frac{Q^2}{2C}\)
where Q is charge and C is a constant.
Use this equation and the information in (a) to determine the SI base units of C.
SI base units …………………………………………………
(ii) Measurements of a constant current in a wire are taken using an analogue ammeter.
For these measurements, describe one possible cause of:
1. a random error
2. a systematic error.
Answer/Explanation
Answer:
(a) (work =) force × displacement
units: \(kg m s^{–2} × m = kg m^2 s^{–2}\)
(b) (i) units of Q: As
units of \(C: kg^{–1} m^{–2} A^2 s^4\)
(ii) 1. e.g. reading scale from different angles
(wrongly) interpolating between scale readings/divisions
2. e.g. zero error
wrongly calibrated scale
Question
(a) State Newton’s second law of motion.
(b) A delivery company suggests using a remote-controlled aircraft to drop a parcel into the garden of a customer. When the aircraft is vertically above point P on the ground, it releases the parcel with a velocity that is horizontal and of magnitude 5.4m/s. The path of the parcel is shown in Fig. 2.1.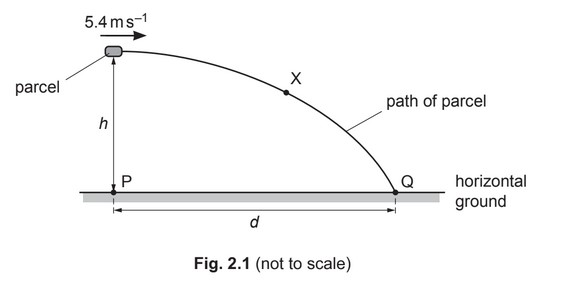
The parcel takes a time of 0.81s after its release to reach point Q on the horizontal ground.
Assume air resistance is negligible.
(i) On Fig. 2.1, draw an arrow from point X to show the direction of the acceleration of the parcel when it is at that point.
(ii) Determine the height h of the parcel above the ground when it is released.
h = …………………………………………….. m
(iii) Calculate the horizontal distance d between points P and Q.
d = …………………………………………….. m
(c) Another parcel is accidentally released from rest by a different aircraft when it is hovering at a great height above the ground. Air resistance is now significant.
(i) On Fig. 2.2, draw arrows to show the directions of the forces acting on the parcel as it falls vertically downwards. Label each arrow with the name of the force.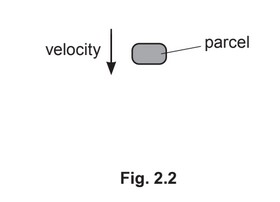
(ii) By considering the forces acting on the parcel, state and explain the variation, if any, of the acceleration of the parcel as it moves downwards before it reaches constant (terminal) speed.
(iii) Describe the energy conversion that occurs when the parcel is falling through the air at constant (terminal) speed.
Answer/Explanation
Answer:
(a) (resultant) force proportional to rate of change of momentum
(b) (i) arrow drawn vertically downwards from point X
(ii) \(s = ut + 1/2at^2\)
\(h = 1/2 \times 9.81 \times 0.81^2\)
= 3.2 m
(iii) \(d = 5.4 \times 0.81\)
= 4.4 m
(c) (i) downward pointing arrow labelled weight
upward pointing arrow labelled weight
(ii) air resistance increases
weight constant or resultant force decreases
(so) acceleration decreases
(iii) gravitational potential energy to thermal/internal energy
Question
(a) State two conditions for an object to be in equilibrium.
1. ……………………………………………………………………………………………………………………………..
2. ……………………………………………………………………………………………………………………………..
(b) A sphere of weight 2.4N is suspended by a wire from a fixed point P. A horizontal string is used to hold the sphere in equilibrium with the wire at an angle of 53° to the horizontal, as shown in Fig. 3.1.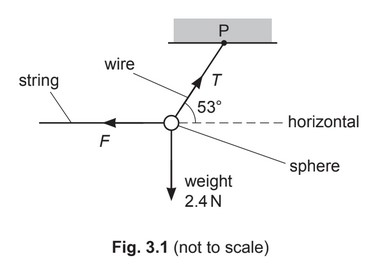
(i) Calculate:
1. the tension T in the wire
T = …………………………………………………… N
2. the force F exerted by the string on the sphere.
F = …………………………………………………… N
(ii) The wire has a circular cross-section of diameter 0.50mm. Determine the stress σ in the wire.
σ = ……………………………………………. Pa
(c) The string is disconnected from the sphere in (b). The sphere then swings from its initial rest position A, as illustrated in Fig. 3.2.
The sphere reaches maximum speed when it is at the bottom of the swing at position B. The distance between P and the centre of the sphere is 75cm.
Air resistance is negligible and energy losses at P are negligible.
(i) Show that the vertical distance h between A and B is 15cm.
(ii) Calculate the change in gravitational potential energy of the sphere as it moves from A to B.
change in gravitational potential energy = ……………………………………………… J
(iii) Use your answer in (c)(ii) to determine the speed of the sphere at B.
Show your working.
speed = ………………………………………… \(ms^{–1}\)
Answer/Explanation
Answer:
(a) resultant force (in any direction) is zero
resultant torque/moment (about any point) is zero
(b) (i) 1. T sin 53° = 2.4
T = 3.0 N
2. F =
T cos 53° or \(F^2 = T^2 – 2.4^2\)
F = 1.8 N
(ii) σ = T / A or σ = F / A
\(A = π d^2 / 4 or A = πr^2\)
\(σ = 3.0 × 4 / [π × (0.50 × 10^{–3})^2]\)
= \(1.5 × 10^7\) Pa
(c) (i) h = 75 – 75 sin 53° = 15 cm
(ii) (Δ)E = mg(Δ)h or ( Δ)E = W(Δ)h
(Δ)E = 2.4 × 15 × \(10^–2\)
= 0.36 J
(iii) \(E = 1/2 mv^2\)
\(0.36 – 1/2 \times (2.4/ 9.81) \times v^2\)
\(v = 1.7 ms^{-1}\)
Question
(a) (i) By reference to the direction of propagation of energy, state what is meant by a longitudinal wave.
(ii) State the principle of superposition.
(b) The wavelength of light from a laser is determined using the apparatus shown in Fig. 4.1.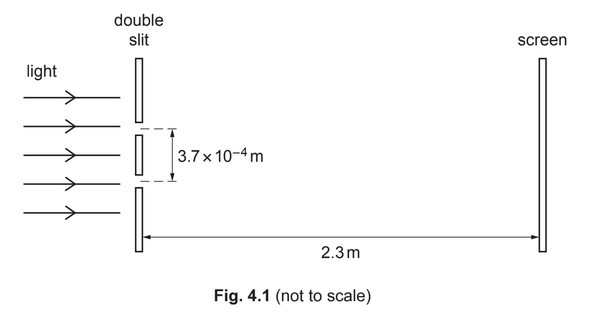
The light from the laser is incident normally on the plane of the double slit. The separation of the two slits is \(3.7×10^{–4}\)m. The screen is parallel to the plane of the double slit. The distance between the screen and the double slit is 2.3m. A pattern of bright fringes and dark fringes is seen on the screen. The separation of adjacent bright fringes on the screen is \(4.3×10^{–3}\)m.
(i) Calculate the wavelength, in nm, of the light.
wavelength = …………………………………………… nm
(ii) The intensity of the light passing through each slit was initially the same. The intensity of the light through one of the slits is now reduced.
Compare the appearance of the fringes before and after the change of intensity.
Answer/Explanation
Answer:
(a) (i) vibrations (of particles) are parallel to direction of energy propagation
(ii) waves meet/overlap (at a point)
(b)(i) λ = ax / D
\(= (3.7 × 10^{–4} × 4.3 × 10^{–3}) / 2.3\)
\( = 6.9 \times 10^{-7}\) (m)
= 690 nm
(ii) • no change to fringe separation/fringe width/number of fringes
• bright fringes are darker
• dark fringes are brighter
Any two marking points, 1 mark each
Question
(a) Metal wire is used to connect a power supply to a lamp. The wire has a total resistance of
3.4Ω and the metal has a resistivity of \(2.6 × 10^{–8}Ωm\). The total length of the wire is 59m.
(i) Show that the wire has a cross-sectional area of \(4.5 × 10^{–7}m^2\).
(ii) The potential difference across the total length of wire is 1.8V.
Calculate the current in the wire.
current = ………………………………………………
(iii) The number density of the free electrons in the wire is \(6.1×10^{28}m^{–3}\).
Calculate the average drift speed of the free electrons in the wire.
average drift speed = ………………………………………… \(ms^{–1}\)
(b) A different wire carries a current. This wire has a part that is thinner than the rest of the wire, as
shown in Fig. 5.1.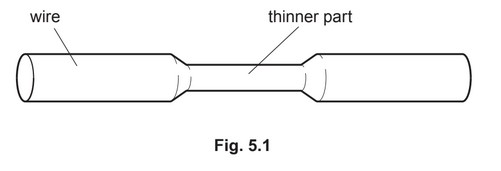
(i) State and explain qualitatively how the average drift speed of the free electrons in the
thinner part compares with that in the rest of the wire.
(ii) State and explain whether the power dissipated in the thinner part is the same, less or
more than the power dissipated in an equal length of the rest of the wire.
(c) Three resistors have resistances of 180Ω, 90Ω and 30Ω.
(i) Sketch a diagram showing how two of these three resistors may be connected together
to give a combined resistance of 60Ω between the terminals shown.
Ensure you label the values of the resistances in your diagram.
(ii) A potential divider circuit is produced by connecting the three resistors to a battery of
electromotive force (e.m.f.) 12V and negligible internal resistance. The potential divider
circuit provides an output potential difference \(V_{OUT}\) of 8.0V.
Fig. 5.2 shows the circuit diagram.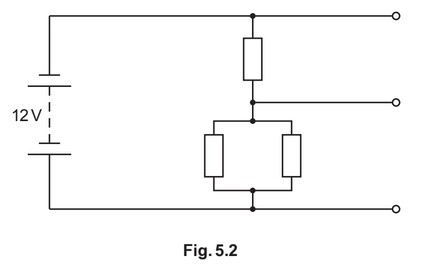
On Fig. 5.2, label the resistances of all three resistors and the potential
difference \(V_{OUT}\).
Answer/Explanation
Answer:
(a) (i) R = ρL / A
\(A = (2.6 × 10^{–8} × 59) / 3.4 = 4.5 × 10^{–7} m^2\)
(ii) I = 1.8 / 3.4
= 0.53 A
(iii) I = Anvq
\(v = 0.53 / (4.5 × 10^{–7} × 6.1 × 10^{28} × 1.60 × 10^{–19})\)
\(= 1.2 × 10^{–4} m s^{–1}\)
(b) (i) (cross-sectional) area/A is less
(I, n, e the same so) average drift speed is greater
(ii) (area is less so) more resistance/R
(I is the same, so) more power/P
or
(P = I2ρL / A so) P ∝ 1 / A(A is less so) more P
(c)(i) 180 Ω and 90 Ω resistors shown connected in parallel
(ii) resistors connected in parallel labelled as 180 Ω and 90 Ω and the other resistor labelled as 30 Ω
\(V_{OUT}\) or 8.0 V labelled across the two resistors in parallel
Question
(a) Two horizontal metal plates are separated by a distance of 2.0cm in a vacuum, as shown in
Fig. 6.1.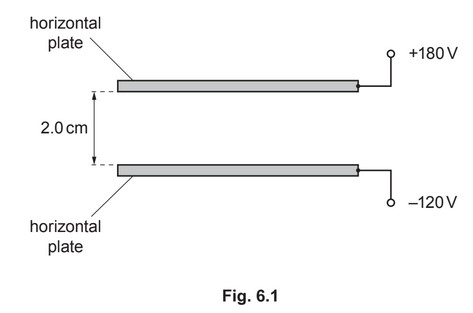
The top plate has an electric potential of +180V and the bottom plate has an electric potential
of –120V.
(i) Determine the magnitude of the electric field strength between the plates.
electric field strength = ……………………………………….. \(NC^{–1}\)
(ii) State the direction of the electric field.
(b) An uncharged atom of uranium-238 (\(^{238}_{92} U\)) has a change made to its number of orbital
electrons. This causes the atom to change into a new particle (ion) X that has an overall
charge of +2e, where e is the elementary charge.
(i) Determine the number of protons, neutrons and electrons in the particle (ion) X.
number of protons = ………………………………………………………
number of neutrons = ……………………………………………………….
number of electrons = ……………………………………………………….
(ii) The particle (ion) X is in the electric field in (a) at a point midway between the plates.
Determine the magnitude of the electric force acting on X.
force = …………………………………………….. N
(iii) The nucleus of uranium-238 \((^{238}_{92}U)\) decays in stages, by emitting α-particles and \(β^–\) particles, to form a nucleus of thorium-230 \((^{230}_{90}Th)\).
Calculate the total number of α-particles and the total number of \(β^–\) particles that are
emitted during the decay of uranium-238 to thorium-230.
number of α-particles = ………………………………………………………
number of β– particles = ………………………………………………………
Answer/Explanation
Answer:
(a) (i) E = ΔV / Δ d
\(E = (180 + 120) / (2.0 × 10^{–2})\)
\(= 1.5 × 10^4 N C^{–1}\)
(ii) vertically downwards
(b) (i) number of protons = 92
number of neutrons = 146
number of electrons = 90
(ii) F = EQ
\(= 1.5 × 10^4 × 2 × 1.60 × 10^{–19}\)
\(= 4.8 × 10^{–15}\) N
(iii) number of α-particles = 2
number of \(β^–\) particles = 2
