Question
(a) Define density.
…………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(b) Fig. 1.1 shows a solid pyramid with a square base.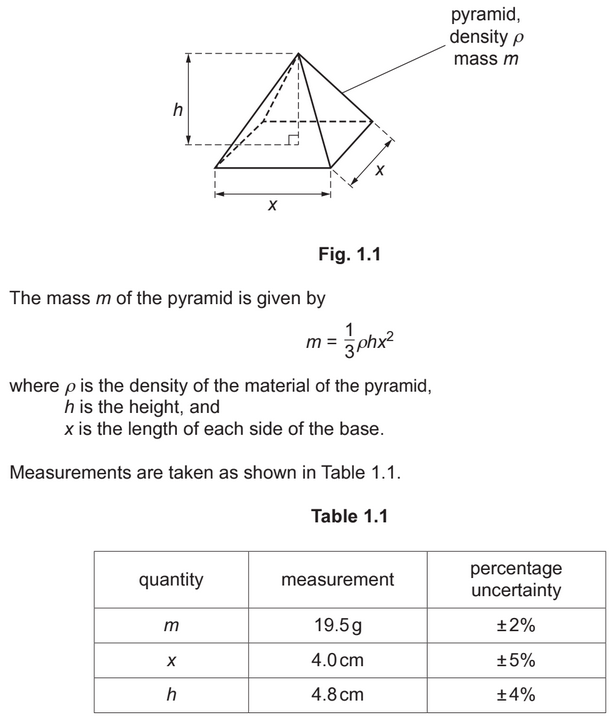
(i) Calculate the absolute uncertainty in length x.
(ii) The density ρ is calculated from the measurements in Table 1.1.
Determine the percentage uncertainty in the calculated value of ρ.
percentage uncertainty = …………………………………………….. %
(c) The square base of the pyramid in (b) rests on the horizontal surface of a bench.
Use data from Table 1.1 to calculate the average pressure of the pyramid on the surface of
the bench. The uncertainty in your answer is not required.
Answer/Explanation
Ans:
(a) mass / volume
(b)(i) absolute uncertainty = 4.0 × (5 / 100)
= (±) 0.2 cm
(b)(ii) percentage uncertainty = 2 + 4 + (5× 2)
= (±) 16%
Question
A person uses a trolley to move suitcases at an airport. The total mass of the trolley and suitcases is 72kg.
(a) The person pushes the trolley and suitcases along a horizontal surface with a constant speed of 1.4 m/s and then releases the trolley. The released trolley moves in a straight line and comes to rest. Assume that a constant total resistive force of 18N opposes the motion of the trolley and suitcases.
(i) Calculate the power required to overcome the total resistive force on the trolley and suitcases when they move with a constant speed of 1.4ms–1.
power = …………………………………………….. W
(ii) Calculate the time taken for the trolley to come to rest after it is released.
time = ……………………………………………… s
(b) At another place in the airport, the trolley and suitcases are on a slope, as shown in Fig. 2.1.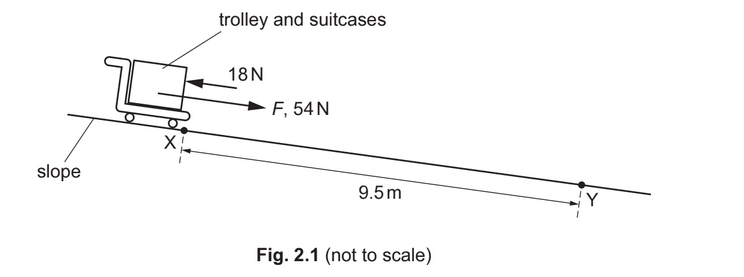
The person releases the trolley from rest at point X. The trolley moves down the slope in a straight line towards point Y. The distance along the slope between points X and Y is 9.5m. The component F of the weight of the trolley and suitcases that acts along the slope is 54N. Assume that a constant total resistive force of 18N opposes the motion of the trolley and suitcases.
(i) Calculate the speed of the trolley at point Y.
speed = ………………………………………… ms–1
(ii) Calculate the work done by F for the movement of the trolley from X to Y.
work done = ……………………………………………… J
(iii) The trolley is released at point X at time t = 0.
On Fig. 2.2, sketch a graph to show the variation with time t of the work done by F for the
movement of the trolley from X to Y.
Numerical values of the work done and t are not required.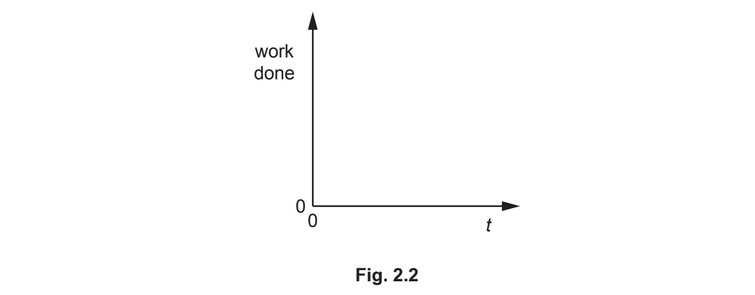
(c) The angle of the slope in (b) is constant. The frictional forces acting on the wheels of the moving trolley are also constant.
Explain why, in practice, it is incorrect to assume that the total resistive force opposing the motion of the trolley and suitcases is constant as the trolley moves between X and Y.
………………………………………………………………………………………….. [1]
Answer/Explanation
Ans:
(a)(i) P = Fv
= 18× 1.4
= 25W
(a)(ii) a =F / m
a = 18 / 72 = 0.25 \((m s^{–2})\)
t = 1.4 / 0.25 = 5.6 s
(b)(i) a = (54– 18) / 72 or 36 / 72 (= 0.50 \(m s^{–2})\)
\(v^2\) = 2× 0.50× 9.5
v = 3.1 \(m s^{–1}\)
(b)(ii) W = 54 × 9.5
= 510 J
(b)(iii) curved line from the origin
gradient of line increases
(c) (force due to) air resistance increases/changes/not constant or air resistance increases with speed
Question
A pendulum consists of a solid sphere suspended by a string from a fixed point P, as shown in Fig. 3.1.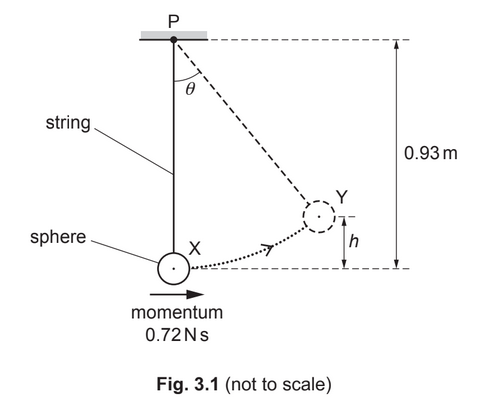
The sphere swings from side to side. At one instant the sphere is at its lowest position X, where it has kinetic energy 0.86J and momentum 0.72Ns in a horizontal direction. A short time later the sphere is at position Y, where it is momentarily stationary at a maximum vertical height h above position X.
The string has a fixed length and negligible weight. Air resistance is also negligible.
(a) On Fig. 3.1, draw a solid line to represent the displacement of the centre of the sphere at position Y from position X. [1]
(b) Show that the mass of the sphere is 0.30kg.
(c) Calculate height h.
h = …………………………………………….. m [2]
(d) The distance between point P and the centre of the sphere is 0.93m. When the sphere is at position Y, the string is at an angle θ to the vertical. Show that θ is 47°. [1]
(e) For the sphere at position Y, calculate the moment of its weight about point P.
moment = ………………………………………….. Nm [2]
(f) State and explain whether the sphere is in equilibrium when it is stationary at position Y.
……………………………………………………………………………………………………………………………
Answer/Explanation
Ans:
(a) solid straight line drawn between centre of sphere at X and at Y
(b) 
(c) (Δ)E = mg(Δ)h
h = 0.86 / (0.30 × 9.81)
= 0.29 m
(d) cos θ = (0.93 – 0.29) / 0.93 so θ = 47°
(e) 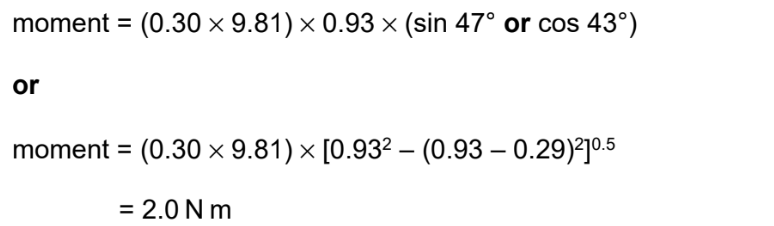
(f) there is a resultant force (acting on sphere)
or
there is a resultant moment (about P acting on pendulum)
(so) not in equilibrium
Question
(a) For a progressive wave, state what is meant by wavelength.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………… [1]
(b) A light wave from a laser has a wavelength of 460nm in a vacuum.
Calculate the period of the wave.
period = ……………………………………………… s [3]
(c) The light from the laser is incident normally on a diffraction grating.
Describe the diffraction of the light waves at the grating.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………… [2]
(d) A diffraction grating is used with different wavelengths of visible light. The angle θ of the
fourth-order maximum from the zero-order (central) maximum is measured for each
wavelength. The variation with wavelength λ of sinθ is shown in Fig. 4.1.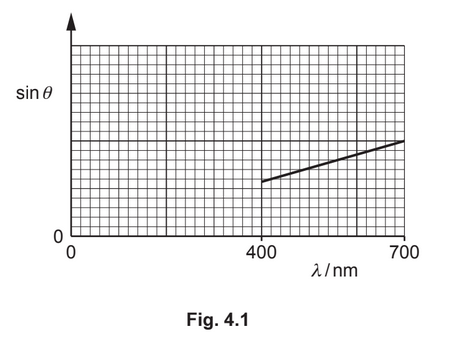
(i) The gradient of the graph is G.
Determine an expression, in terms of G, for the distance d between the centres of two
adjacent slits in the diffraction grating.
d = …………………………………………………
(ii) On Fig. 4.1, sketch a graph to show the results that would be obtained for the
second-order maxima.
Answer/Explanation
Ans:
(a) distance moved by wavefront/energy during one cycle/oscillation/period (of source)
or
minimum distance between two wavefronts
or
distance between two adjacent wavefronts
(b) v =λ / T
or
v = fλ and f = 1 / T
\(T = 460 \times 10^{–9} / 3.00 \times 10^8 \)
\(= 1.5\times 10^{–15} s\)
(c) waves pass through/enter the slit(s)
waves spread (into geometric shadow) B1
(d)(i) n λ = d sin θ
G = sin θ / λ
d = 4 / G
(d)(ii) straight line from 400 nm to 700 nm that is always below printed line
straight line has smaller gradient than printed line and is 5 small squares high at wavelength of 700 nm
Question
(a) State Kirchhoff’s second law.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(b) A battery has electromotive force (e.m.f.) 4.0V and internal resistance 0.35Ω. The battery is
connected to a uniform resistance wire XY and a fixed resistor of resistance R, as shown in
Fig. 5.1.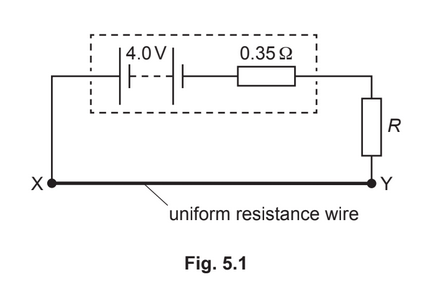
Wire XY has resistance 0.90Ω. The potential difference across wire XY is 1.8V.
Calculate:
(i) the current in wire XY
current = ……………………………………………… A [1]
(ii) the number of free electrons that pass a point in the battery in a time of 45s
number = …………………………………………………
(iii) resistance R.
R = …………………………………………….. Ω
(c) A cell of e.m.f. 1.2V is connected to the circuit in (b), as shown in Fig. 5.2.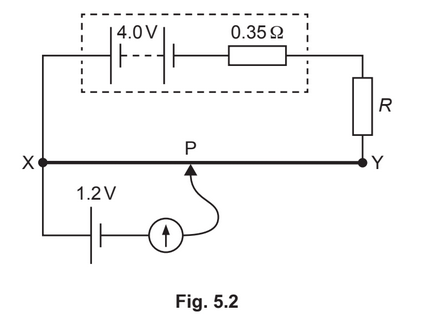
The connection P is moved along the wire XY. The galvanometer reading is zero when
distance XP is 0.30m.
(i) Calculate the total length L of wire XY.
L = …………………………………………….. m [2]
(ii) The fixed resistor is replaced by a different fixed resistor of resistance greater than R.
State and explain the change, if any, that must be made to the position of P on wire XY
so that the galvanometer reading is zero.
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………….
Answer/Explanation
Ans:
(a) sum of e.m.f.(s) = sum of p.d.(s)
or
(algebraic) sum of e.m.f.(s) and p.d.(s) is zero
around a loop/around a closed circuit
(b)(i) I = 1.8 / 0.90= 2.0A
(b)(ii) Q =It
number \(= (2.0\times 45) / 1.60\times 10^{–19}= 5.6 \times 10^{20}\)
(b)(iii) 4.0 = 1.8 + [2.0× (0.35 +R)]
or
4.0 = 2.0× (0.90 + 0.35 +R)
R = 0.75Ω
(c)(i) 1.2 / 1.8 = 0.30 / L
L = 0.45 m
(c)(ii) p.d. across XY decreases/p.d. across XP decreases
(so) P is moved towards Y/away from X/to the right
Question
(a) A proton in a nucleus decays to form a neutron and a \(β^+\) particle.
(i) State the name of another lepton that is produced in the decay.
……………………………………………………………………………………………………………………. [1]
(ii) State the name of the interaction (force) that gives rise to this decay.
……………………………………………………………………………………………………………………. [1]
(iii) State which of the three particles (proton, neutron or \(β^+\) particle) has the largest ratio of
charge to mass.
……………………………………………………………………………………………………………………. [1]
(iv) Use the quark model to show that the charge on the proton is +e, where e is the
elementary charge.
[2]
(v) The quark composition of the proton is changed during the decay.
Describe the change to the quark composition.
………………………………………………………………………………………………………………………….
……………………………………………………………………………………………………………………. [1]
(b) A nucleus X ![]() and a nucleus Y
and a nucleus Y ![]() are accelerated by the same uniform electric field.
are accelerated by the same uniform electric field.
(i) Determine the ratio

ratio = …………………………………………………
(ii) Determine the ratio
ratio = …………………………………………………
(iii) Nucleus X is at rest in the uniform electric field at time t = 0.
The field causes nucleus X to accelerate so that it moves through the field.
On Fig. 6.1, sketch the variation with time t of the acceleration a of nucleus X due to the
field.
Answer/Explanation
Ans:
(a)(i) (electron) neutrino
(a)(ii) weak (nuclear force/interaction)
(a)(iii) \(β^+\) (particle)
(a)(iv) (quark structure is) up up down or uud
\((2 / 3)e + (2 / 3)e– (1 / 3)e = (+)e \)
(a)(v) up up down changes to up down down or uud→ udd
or
up changes to down or u→ d
(b)(i) F = Eq C
ratio = 6 / 8 = 0.75
(b)(ii) ratio = 0.75 × (16 / 12) = 1.0
(b)(iii) horizontal straight line at a non-zero value of a
