Questions 1
Topic – 1.3
(a) The list below shows some SI quantities.
Underline the quantity that is not an SI base quantity.
charge current length time
(b) A square solar panel with sides of length 1300mm is shown in Fig. 1.1.
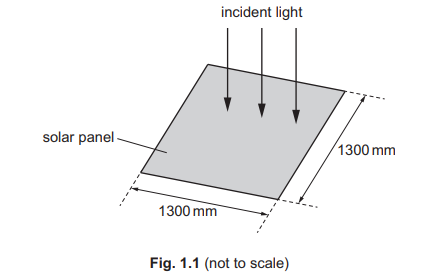
Light is incident normally on the solar panel.
(i) The power of the light incident on the solar panel is 750W. Calculate the intensity of the light.
(ii) The percentage uncertainty in the incident power is ±3%. The uncertainty in the length of each side is ±5mm. Calculate the percentage uncertainty in the intensity of the light.
(iii) The useful power output of the solar panel is 160W. Calculate the percentage efficiency of the solar panel.
(iv) Another square solar panel is placed so that light of the same intensity is incident normally on it. The new panel has shorter sides than the original panel. The new panel has the same power output as the original panel. State and explain whether the efficiency of the new panel is greater than, less than or the same as the efficiency of the original panel.
▶️Answer/Explanation
Ans
(a) charge underlined (and no others)
(b)(i)
I =P / A
= \(750 / (1300\times 10^{–3})^2\)
= 440\(Wm^{–2}\)
(ii) percentage uncertainty = \(3 + 2\times (5 / 1300)\times 100\)
= \(3 + 2\times 0.38\)
= (±) 4%
(iii) efficiency = useful output power / total input power
= \((160 / 750)\times 100\)
= 21%
(iv) area (of the new panel) is less
input power (of the new panel) is less (than the input power of the original panel) (as intensity is constant)
(useful power output is unchanged so) efficiency is greater (than the original panel)
Questions 2
Topic – 2.1
A skydiver jumps from an aircraft at time t = 0 and falls vertically downwards. The variation with t of her velocity v is shown in Fig. 2.1.
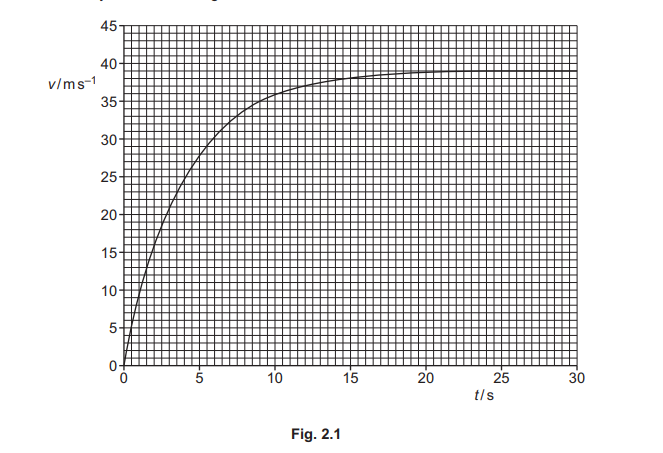
(b) The mass of the skydiver and her equipment is 68kg. The upthrust on the skydiver is negligible. After reaching terminal velocity, the skydiver opens her parachute at time \(t_1\). A total drag force of 1800N acts on the skydiver. Determine the magnitude and direction of the acceleration of the skydiver at time \(t_1\).
(c) The parachute is fully open at time \(t_2\). At a later time \(t_3\) the skydiver reaches a constant velocity of \(5.7ms^{–1}\).
(i) Describe and explain the variation with time of the magnitude of her acceleration between
time \(t_2\) and time \(t_3\).
(ii) Calculate the change in momentum of the skydiver between time \(t_1\) and time \(t_3\).
▶️Answer/Explanation
Ans
(a)(i) 39 \(ms^{–1}\)
Questions 3
Topic – 6.1
Lightning occurs when charge builds up in the atmosphere, creating a potential difference between the ground and the atmosphere. During a lightning strike there is an average current of \(3.3 × 10^4\)A for a time of \(2.6 × 10^{–5}\) s.
(a) Calculate the charge transferred during the lightning strike.
(b) The potential difference between the ground and the atmosphere is \(3.0 × 10^7V\). Calculate the average power, in GW, transferred during the lightning strike.
(c) A lightning rod is attached to a tall building to conduct charge safely to the ground. The lightning rod is modelled as a uniform cylindrical copper cable of total length 95m that runs from the ground to the top of the building, as shown in Fig. 3.1.
(i) The resistance of the lightning rod is 9.6Ω. The resistivity of copper is \(1.7 × 10^{–8}\)Ωm. Determine the radius of the lightning rod.
(ii) The radius of the copper lightning rod is doubled with no change to its length. State the effect of this change on the resistance of the lightning rod.
(d) A section of the lightning rod of length 0.12m is removed for testing. A tensile stress of \(1.9 × 10^6\)Pa is applied, as shown in Fig. 3.2.
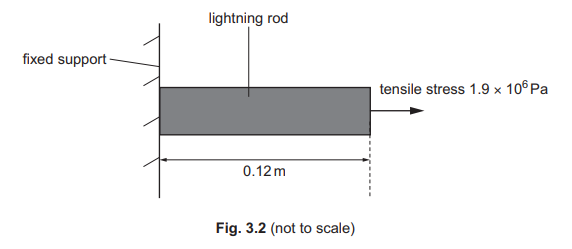The section of the rod obeys Hooke’s law. The Young modulus of copper is \(1.3 × 10^{11}\)Pa. Calculate the extension of the section.
▶️Answer/Explanation
Ans
Questions 4
Topic – 6.2
A pinball machine uses a spring to launch a small metal ball of mass \(4.5 × 10^{–2}\) kg up a ramp. The spring is compressed by \(8.0 × 10^{–2}\)m and held in equilibrium, as shown in Fig. 4.1.
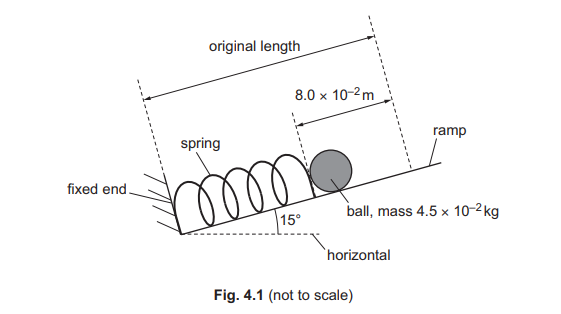
The ramp is at an angle of 15° to the horizontal.
(a) The spring obeys Hooke’s law and has a spring constant of \(29Nm^{–1}\). Calculate the elastic potential energy in the compressed spring.
(b) The spring is released and expands quickly back to its original length.
(i) Calculate the increase in gravitational potential energy of the ball when the spring returns to its original length.
(ii) The ball leaves the spring when the spring reaches its original length. Assume that all the elastic potential energy of the spring is transferred to the ball. Calculate the speed of the ball as it leaves the spring.
(c) The ball comes to rest on a horizontal trapdoor of negligible mass at a distance d from its pivot. A force F acts vertically downwards at a distance of 2.0cm from the pivot, as shown in Fig. 4.2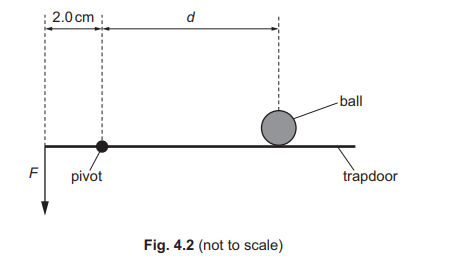 
(i) The trapdoor is in equilibrium when F is 1.7N. Calculate d.
(ii) Force F is decreased from 1.7N. State the direction of the resultant moment about the pivot on the trapdoor.
▶️Answer/Explanation
Ans
Questions 5
Topic – 10.2
(a) State Kirchhoff’s second law.
(b) A battery of electromotive force (e.m.f.) 9.0V and negligible internal resistance is connected in series with a variable resistor X and a thermistor Y as shown in Fig. 5.1.
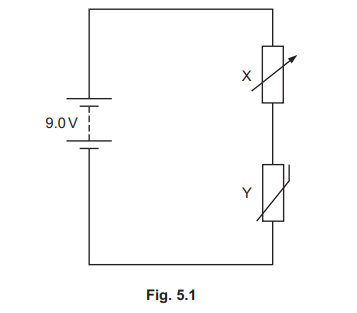
Fig. 5.2 shows the relationship between temperature and resistance for the thermistor.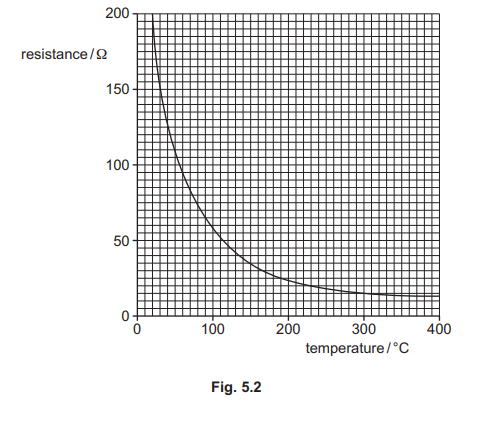 
(i) The current in the circuit is \(1.1 × 10^{–2}A\). The potential difference across Y is 4.0V. Calculate the resistance of X.
(ii) The temperature of Y is changed to 190°C. The resistance of X remains unchanged. Determine the new potential difference across Y
(iii) The resistance of X is increased. The temperature of Y remains at 190°C. By reference to the current in the circuit, state and explain the effect of this change, if any, on the potential difference across Y.
▶️Answer/Explanation
Ans
(a) sum of electromotive force(s) = sum of potential difference(s) around a (closed) loop.
(b)(i) R =V / I
= \((9.0 – 4.0) / 1.1\times 10^{–2}\)
= \(450 \Omega\)
(ii) resistance (of thermistor) = 25 (\(\Omega\) ) (from graph)
(iii) (resistance of X increases so) the total resistance increases
current decreases
potential difference (across thermistor / Y) decreases
Questions 6
Topic – 17.1
Light of a single frequency is incident normally on a diffraction grating. An interference pattern of bright and dark fringes forms on the semicircular screen shown in Fig. 6.1.
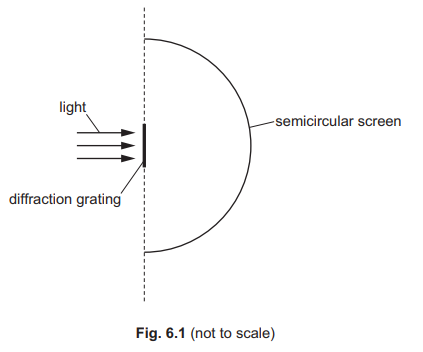
The light has wavelength 520nm. The separation of the lines in the grating is \(3.8 × 10^{–6}m\).
(a) Determine the total number of bright fringes formed on the screen.
(b) The light is replaced with red light of a single frequency.
(i) State whether the frequency of the red light is greater than, less than or the same as the frequency of the original light.
(ii) State and explain the effect of this change on the number of bright fringes formed on the screen. A calculation is not required.
▶️Answer/Explanation
Ans
(a)\(n \lambda = d sin \theta\)
n = \((3.8 \times 10^{–6} \times sin 90°) / (520\times 10^{–9})\)
( = 7.3)
number of bright fringes formed = 15 (given as an integer)
(b)(i) (frequency of red light is) less (than frequency of original light)
(ii) (red light has) longer wavelength
(so) number (of bright fringes formed) is less / fewer (bright fringes are formed)
Questions 7
Topic – 11.2
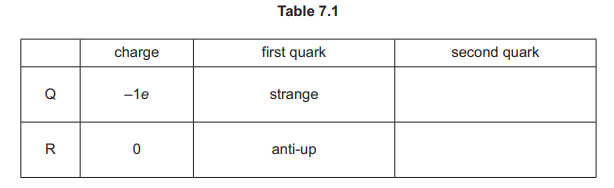
A particle Q and a particle R are each composed of one quark and one antiquark.
(a) State the name of the class (group) of particles that includes Q and R
b) Q has a charge of –1e, where e is the elementary charge. R has a charge of 0. Complete Table 7.1 to show a possible second quark in each of Q and R.
▶️Answer/Explanation
Ans
(a) meson(s) or hadron(s)
(b) Q: anti-up or anti-charm or anti-top
R: up or charm or top