Question
(a) (i) State what is meant by a field of force.
(ii) Define gravitational field strength.
(b) An isolated planet may be assumed to be a uniform sphere of radius \(3.39 × 10^6\)m with its
mass of \(6.42 × 10^{23}\) kg concentrated at its centre.
Calculate the gravitational field strength at the surface of the planet.
field strength = ………………………………………. \(Nkg^{–1}\)
(c) Calculate the height above the surface of the planet in (b) at which the gravitational field
strength is 1.0% less than its value at the surface of the planet.
height = …………………………………………….. m
Answer/Explanation
Ans:
(a) (i) region (of space)
where a particle experiences a force
(ii) force per unit mass
(b)\(g= GM / R^2\)
\(= (6.67 × 10^{–11} × 6.42 × 10^{23}) / (3.39 × 10^6)^2\)
\(= 3.73 N kg^{-1}\)
(c) \(0.99 × 3.73 = (6.67 × 10^{–11} × 6.42 × 10^{23}) / r^2\)
\(r = 3.41 × 10^6 (m)\)
height = (r – R)
\(= 2 × 10^4\) m
or
\(0.99 × 3.73 = (6.67 × 10^{–11} × 6.42 × 10^{23}) / (R + h)^2\)
\((R+h)^2 = 1.1596 \times 10^{13}\)
\(R + h = 3.41 × 10^6\) (m)
\(h = 2 \times 10^4\) m
or
\(0.99 = (3.39 × 10^6)^2 / r^2\)
\(r = 3.41 × 10^6\) (m)
\(height = 2 × 10^4\) m
Question
(a) The first law of thermodynamics may be expressed as
ΔU = (+q) + (+w)
where ΔU is the increase in internal energy of the system.
State the meaning of:
+q
+w.
(b) The variation with pressure p of the volume V of a fixed mass of an ideal gas is shown in
Fig. 2.1.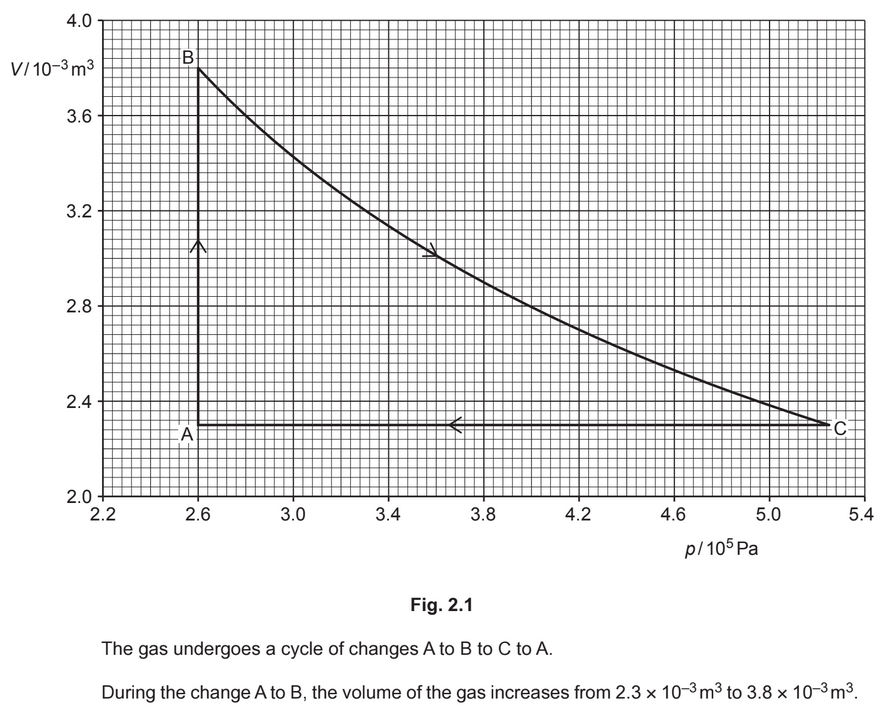
(i) Show that the magnitude of the work done during the change A to B is 390J.
(ii) State and explain the total change, if any, in the internal energy of the gas during one complete cycle.
(c) During the change A to B, 1370J of thermal energy is transferred to the gas.
During the change B to C, no thermal energy enters or leaves the gas. The work done on the
gas during this change is 550J.
Use these data and the information in (b) to complete Table 2.1.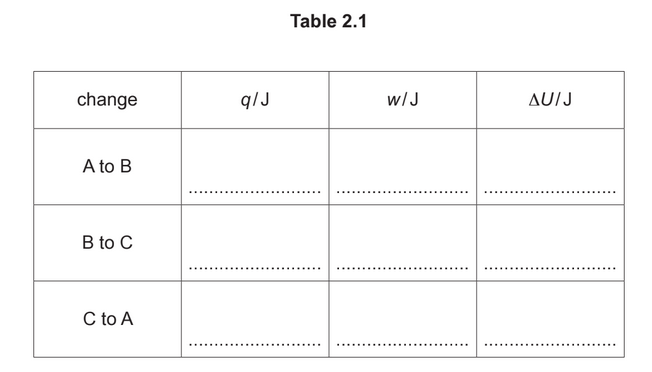
Answer/Explanation
Answer:
(a) +q: thermal energy transfer to system
+w: work done on system
(b) (i) \((W =) 2. 6 ×10^5 × (3.8 – 2.3) × 10^{–3} = 390 J\)
(ii) no (total) change (in internal energy)
gas returns to its original temperature
(c) A to B row all correct (1370, – 390, 980)
B to C row all correct (0, 550, 550)
C to A row:
ΔU adds to the other two ΔU values to give zero
C to A row: w = 0 and q adds to w to give ΔU value
complete correct answer:
Question
A pendulum consists of a metal sphere P suspended from a fixed point by means of a thread, as
illustrated in Fig. 3.1.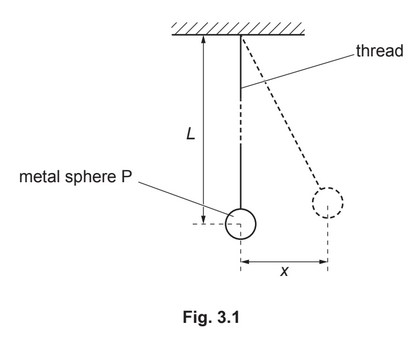
The centre of gravity of sphere P is a distance L from the fixed point.
The sphere is pulled to one side and then released so that it oscillates. The sphere may be
assumed to oscillate with simple harmonic motion.
(a) State what is meant by simple harmonic motion.
(b) The variation of the velocity v of sphere P with the displacement x from its mean position is
shown in Fig. 3.2.
Use Fig. 3.2 to determine the frequency f of the oscillations of sphere P.
f = ……………………………………………. Hz
(c) The period T of the oscillations of sphere P is given by the expression
\(T = 2\pi \sqrt{(\frac{L}{g})}\)
where g is the acceleration of free fall.
Use your answer in (b) to determine the length L.
L = …………………………………………….. m
(d) Another pendulum consists of a sphere Q suspended by a thread. Spheres P and Q are
identical. The thread attached to sphere Q is longer than the thread attached to sphere P.
Sphere Q is displaced and then released. The oscillations of sphere Q have the same
amplitude as the oscillations of sphere P.
On Fig. 3.2, sketch the variation of the velocity v with displacement x for sphere Q.
Answer/Explanation
Answer:
(a) acceleration (directly) proportional to displacement
acceleration in opposite direction to displacement
or
acceleration (directed) towards equilibrium position
(b) \(v = ω(x_0^2 – x^2)^{1⁄2}\) and ω = 2 πf
or
\(v_0 = x_0ω\) and ω = 2 πf
substitution of any correct point from graph, e.g. for
\(x = 0: 0.25 = 2 πf × 8.8 × 10^{–2}\)
f = 0.45 Hz
(c) \(1 / 0.45 = 2 π × ( L / 9.81)^{1⁄2}\)
L = 1.2 m
(d) ellipse about the origin with same intercepts on x-axis
ellipse about the origin crossing v-axis inside original loop
Question
(a) Explain the principles of the generation of ultrasound waves for use in medical diagnosis.
(b) The linear attenuation (absorption) coefficient for a parallel beam of ultrasound waves in air is \(1.2cm^{–1}\).
The parallel beam passes through a layer of air of thickness 3.5cm.
Calculate the ratio, in dB,
ratio = ……………………………………………. dB
Answer/Explanation
Answer:
(a) quartz crystal
alternating p.d. across crystal causes it to vibrate
resonance occurs when frequency of p.d. matches natural frequency of crystal
natural frequency of crystal is in ultrasound range
(b) \(I = I_0 e^{–μx}\)
\(I / I_0 = e^{–1.2 × 3.5}\)
= 0.015
ratio / dB = –10 lg (1 / 0.015) or 10 lg (0.015)
= -18 dB
Question
(a) Define electric potential at a point.
(b) Two point charges A and B are separated by a distance of 12.0cm in a vacuum, as illustrated
in Fig. 5.1.
The charge of A is \(+2.0 × 10^{–9}\)C.
A point P lies on the line joining charges A and B. Its distance from charge A is x.
The variation with distance x of the electric potential V at point P is shown in Fig. 5.2.
Use Fig. 5.2 to determine:
(i) the charge of B
charge = …………………………………………….. C
(ii) the change in electric potential when point P moves from the position where x = 9.0cm to the position where x = 3.0cm.
change = ……………………………………………… V
(c) An α-particle moves along the line joining point charges A and B in Fig. 5.1.
The α-particle moves from the position where x = 9.0cm and just reaches the position where
x = 3.0cm.
Use your answer in (b)(ii) to calculate the speed v of the α-particle at the position where
x = 9.0cm.
v = ………………………………….. \(ms^{-1}\)
Answer/Explanation
Answer:
(a) work done per unit charge
(work done on charge) moving positive charge from infinity
(b) (ii) \((2.0 × 10^{–9}) / 4 πε_0(4.0 × 10^{–2}) + Q / 4 πε_0(8.0 × 10^{–2}) = 0\)
\(Q = 4.0 × 10^{–9}\) C
Q given with negative sign
(ii) change = 1200 V
(c) \(1⁄2mv^2 = qV\)
\(1⁄2 × 4 × 1.66 × 10^{–27} × v^2 = 2 × 1.60 × 10^{–19} × 1200\)
\(v = 3.4 × 10^5 m s^{–1}\)
Question
(a) (i) Define the capacitance of a parallel plate capacitor.
(ii) State three functions of capacitors in electrical circuits.
1.
2.
3.
(b) A student has available four capacitors, each of capacitance 24μF.
The capacitors are connected as shown in Fig. 6.1.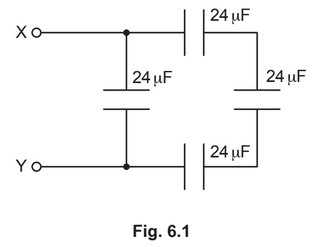
Calculate the combined capacitance between the terminals X and Y
capacitance = ……………………………… \(\mu F\)
Answer/Explanation
Answer:
(a) (i) charge per unit potential (difference)
charge on one plate and potential difference across the plates
(ii) any three points from:
• smoothing
• timing/(time) delay
• tuning
• oscillator
• blocking d.c.
• surge protection
• temporary power supply
(b) (capacitors in series have combined capacitance =) 8 μF
capacitance = 8 + 24
= 32 μF
Question
An ideal operational amplifier (op-amp) is to be used in a comparator circuit.
Part of the comparator circuit is shown in Fig. 7.1.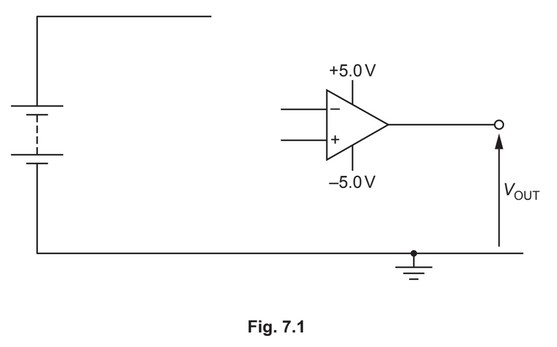
Three resistors, each of resistance 1000Ω, and a negative temperature coefficient thermistor are
available to complete the circuit.
The circuit is to be designed so that, at low temperatures, the output \(V_{OUT}\) is –5.0V and at higher
temperatures, the output \(V_{OUT}\) is to be +5.0V.
(a) On Fig. 7.1, draw the input circuit to the inverting and non-inverting inputs of the op-amp.
(b) State a suitable value for the thermistor resistance when the thermistor is at:
(i) low temperature where \(V_{OUT}\) is –5.0V
(ii) a higher temperature where \(V_{OUT}\) is +5.0V.
Answer/Explanation
Answer:
(a) two resistors connected in series between earth and positive of battery and no extra connections
one resistor and thermistor connected in series between earth and positive of battery and no extra connections
midpoints of the two potential dividers connected, one each, to the op-amp input terminals
thermistor in correct place in potential divider circuit
(either the upper part of the potential divider leading to \(V^+\) or the lower part of the potential divider leading to
\(V^–\))
(b) (i) value greater than 1000 Ω
(ii) non-zero value less than 1000 Ω
Question
A slice of a conducting material has its face QRLK normal to a uniform magnetic field of flux
density B, as illustrated in Fig. 8.1.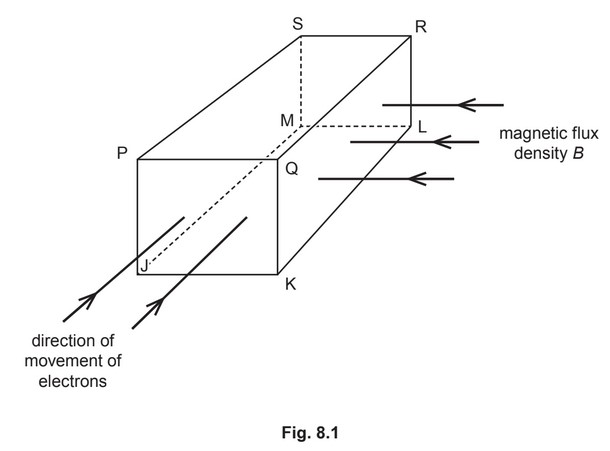
Electrons enter the slice travelling perpendicular to face PQKJ.
(a) For the free electrons moving in the slice:
(i) state the direction of the force on an electron due to movement of the electron in the magnetic field
(ii) identify the faces, using the letters on Fig. 8.1, between which a potential difference is developed.
face …………………………… and face ……………………………
(b) Explain why the potential difference in (a)(ii) reaches a maximum value.
(c) The number of free electrons per unit volume in the slice of material is \(1.3 × 10^{29}m^{–3}\).
The thickness PQ of the slice is 0.10mm.
The magnetic flux density B is \(4.6 × 10^{–3}\)T.
Calculate the potential difference across the slice for a current of \(6.3 × 10^{–4}\)A.
potential difference = ……………………………………………… V
(d) The slice in (c) is a metal.
By reference to your answer in (c), suggest why Hall probes are usually made using
semiconductors rather than metals.
Answer/Explanation
Answer:
(a) (i) downwards
(ii) PQRS and JKLM
(b) (as charge separates) an electric field is created (between opposite faces)
(maximum value is reached when) electric force (on electron) is equal and opposite to magnetic force (on electron)
(c) \(V_H = B I / ntq \)
= \((4.6 × 10^{–3} × 6.3 × 10^{–4}) / (1.3 × 10^{29} × 0.10 × 10^{–3} × 1.60 × 10^{–19})\)
\(= 1.4 \times 10^{-12} V\)
(d) semiconductors have a (much) smaller value for n
\(V_H\) for semiconductors is (much) larger so more easily measured
Question
(a) Define magnetic flux.
(b) A simple transformer consists of two coils of wire wound on a soft-iron core, as illustrated in
Fig. 9.1.
There is a sinusoidal current in the primary coil.
Explain:
(i) how this current gives rise to an induced electromotive force (e.m.f.) in the secondary coil
(ii) why the e.m.f. induced in the secondary coil is not constant.
(c) Explain why the soft-iron core in (b) is laminated.
Answer/Explanation
Answer:
(a) flux density × area
where flux is normal to area
or
flux density × area × sin θ
where θ is angle between flux direction and (plane of) area
(b) (i) (alternating) current creates changing (magnetic) flux
core links (magnetic) flux with secondary coil
changing flux (in secondary) causes induced e.m.f.
(ii) rate of change of flux is not constant
(induced) e.m.f. is proportional to rate of change of flux
(c) reduces induced currents in core
hence reduces energy losses (in core)
Question
(a) Outline briefly the principles of computed tomography (CT scanning).
(b) One section of a model designed to illustrate CT scanning is divided into four voxels.
The pixel numbers K, L, M and N of the voxels are shown in Fig. 10.1.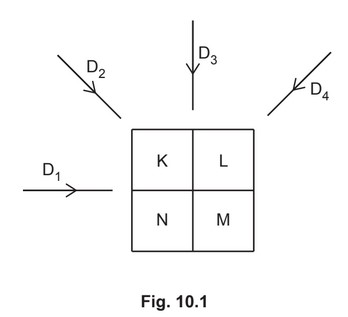
The section is viewed, in turn, from four different directions \(D_1\), \(D_2\), \(D_3\) and \(D_4\), as shown in
Fig. 10.1.
The detector readings for each direction are noted and these are summed to give the values
shown in Fig. 10.2.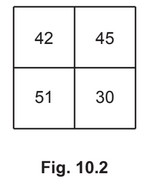
The background reading is 24.
Determine the pixel numbers K, L, M and N shown in Fig. 10.1.
K = ………………………………………………………
L = ………………………………………………………
M = ………………………………………………………
N = ………………………………………………………
Answer/Explanation
Answer:
(a) X-rays are used
section (of object) is scanned
scans/images taken at many angles/directions
or
images of each section are 2-dimensional
(images of (many)) sections are combined
(to give) 3-dimensional image of (whole) structure
(b) K = 6
L = 7
M = 2
N = 9
3 marks: all four correct
2 marks: three correct and one incorrect or all correct with two numbers transposed
1 mark: two correct and two incorrect
Question
A photon of wavelength 540nm collides with an isolated stationary electron, as illustrated in
Fig. 11.1.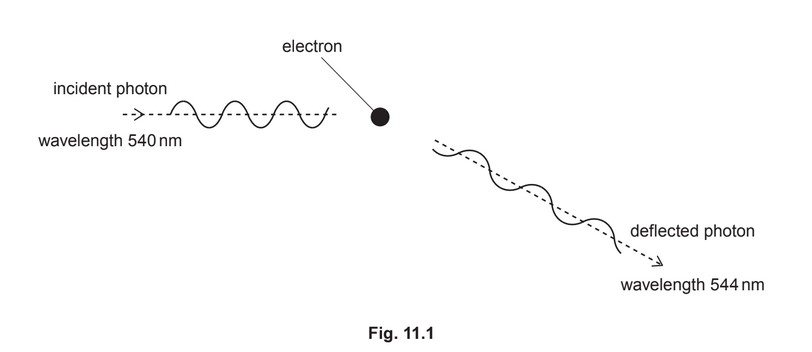
The photon is deflected elastically by the electron.
The wavelength of the deflected photon is 544nm.
(a) (i) State what is meant by a photon.
(ii) On Fig. 11.1, draw an arrow to indicate the approximate direction of motion of the
deflected electron.
(b) Calculate:
(i) the momentum of the deflected photon
momentum = …………………………………………… Ns
(ii) the energy transferred to the deflected electron.
energy = ……………………………………………… J
(c) Another photon of wavelength 540nm collides with an isolated stationary electron.
Explain why it is not possible for the deflected photon to have a wavelength less than 540nm.
Answer/Explanation
Answer:
(a) (i) quantum of energy
of electromagnetic radiation
(ii) arrow (on Fig. 11.1) pointing upwards and to the right
(b) (i) λ = h / p
\(p = (6.63 × 10^{–34}) / (544 × 10^{–9})\)
= \(1.22 × 10^{–27}\) N s
(ii) energy = hc / λ
\(= 6.63 × 10^{–34} × 3.00 × 10^8 × (540^{–1} – 544^{–1}) × 10^9\)
\(= 2.7 × 10^{–21}\) J
(c) (smaller wavelength corresponds to) greater photon energy
any one point from:
• (deflected) photon loses energy (so not possible)
• (deflected) photon would need to gain energy (so not possible)
• electron would need to lose energy (so not possible)
• initially electron energy is zero (so not possible)
Question
Iodine – \((^{131}_{53}I)\) is a radioactive isotope with a decay constant of \(9.9 × 10^{–7} s^{–1}\).
(a) State what is meant by:
(i) radioactive
number =
(ii) decay constant.
(b) Some water becomes contaminated with iodine-131.
The activity of the iodine-131 in 1.0kg of water is 560Bq.
Determine the number of iodine-131 atoms in 1.0kg of water.
number = …………………………………………………
(c) Regulations require that the activity of iodine-131 in 1.0kg of water is to be less than 170Bq.
Calculate the time, in days, for the activity of the contaminated water in (b) to be reduced to
170Bq.
time = ………………………………………… days
Answer/Explanation
Answer:
(a) (i) unstable nucleus
emits ionising radiation or decays spontaneously
(ii) probability of decay (of a nucleus)
per unit time
(b) A = λN
\(560 = 9.9 × 10^{–7} × N\)
\(N = 5.7 × 10^8\)
(c) \(A = A_0 e^{–λt}\)
\(170 = 560 exp(–9.9 × 10^{–7} × t)\)
\(t = 1.2 × 10^6 s\)
= 14 days
